Find the volume common to two circular cylinders, each with radius r, if the axes of the cylinders intersect at right angles. (using disk/washer)
I saw no example of this problem anywhere.. I saw an example how to solve it without calculus but I'm afraid that'll be deductions on my test.. I have the volume of a cylinder and the method of area between two curves but this is out of my reach.... I don't know what I can try...
The main challenge in this problem is to predict the solid itself. Take a look at the image below
As we increase the height $z$ of the intersecting plane the section of the solid is a square with a side $a$. Since the solid is created with two cylinders of radius $r$, $a$ and $z$ are related by $$a^2+z^2=r^2$$
The area of the square is $A=a^2$ or in terms of $z$: $$A(z)=a^2=r^2-z^2$$ The method of washers tells us $$V=8\int_0^rA(z)dz=8\int_0^r(r^2-z^2)dz=8\left(r^3-\frac{r^3}{3}\right)=\frac{16}{3}r^3$$
Note that the coefficient $8$ is required since we are considering a $1/8$th part of the solid.
this link gives proper visualisation of intersection of 2 cylinders having same radii. Volume is calculated by 2 different methods.
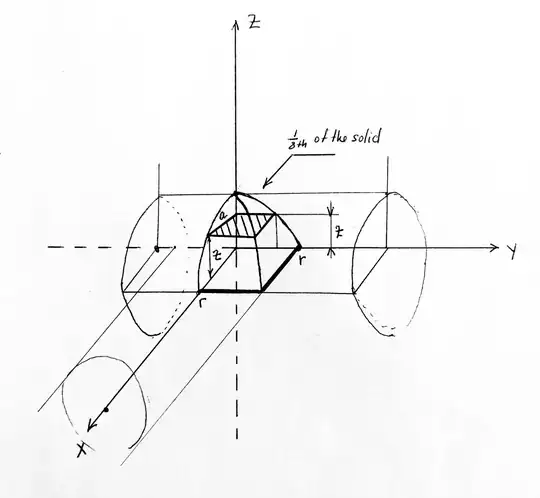
Let r bet the radius of both cylinders and their axes are both perpendicular and intersecting. There is a common sphere enveloped by the 2 intersecting cylinders. If we look at the planar section which passes through both cylinder axes we can see a square area common to both cylinders. This square has an area of (2.r.2.r). We can also see a circle which is produced as a result of the plane passing through the enveloped common sphere. This circle has an area of (Pi.r.r).
If the plane is moved away from the cylinders axes, the intersection surface will reduce until the plane exits the cylinders completely. During this transition an ever changing common surface area is produced, but it will always consist of a square with a circle inside it which is tangential to that square at the middle of each side of the square. The ratio of the square to the circle is (4.r.r)/(pi.r.r)= 4/pi.
We know the volume of the common sphere is (4.Pi.r.r.r/3),So by using a similar shape approach, we can deduce that the common volume of the intersecting cylinders will be (4.Pi.r.r.r/3).(4/Pi)= 16.r.r.r/3 There is no Pi in the answer. hope that's useful, and no Calculus either. Lol.
These are some hints: Consider the two following cylinders: $y^2+z^2=1$ and $x^2+z^2=1$. Let $\mathcal{C}$ be the region common to both:
a) Can you explain why the volume is between $\frac{4}{3}\pi$ and $8$?
b)What section is obtained when $\mathcal{C}$ is sliced by a plane that is parallel to the $xy$-plane?
c)Integrate to find the volume.
The derivation above looks good. This volume is known as a "Steinmetz Solid." There is a page discussing its properties at Mathworld. That page shows another way to get the volume by integration.
Using prismoidal formula. Area at the Middle of the intersectcion is a square with sides 2r, so the area is 4r^2. Then the area at the top and bottom is 0. The length of the area of intersection is the diameter of cylinder equal to 2r.
Prismoidal formula. V= L*(Atop +4Amid + Abot)/6 V= 2r(0+4*4r^2+0)/6 =(16/3) * r^3
The volume of a Steinmetz solid $(SS)$, formed by the intersection of $2$ cylinders (radii $r$) at right angles is:
$$V = 4r \cdot r \cdot r \left(\frac{\pi}{2} - \frac{1}{3}\right) = 4r^3\left(\frac{\pi}{2} - \frac{1}{3}\right)$$
As the volume of $SS$ is formed by sections of a cylinder, the answer must contain $\pi$.
