5

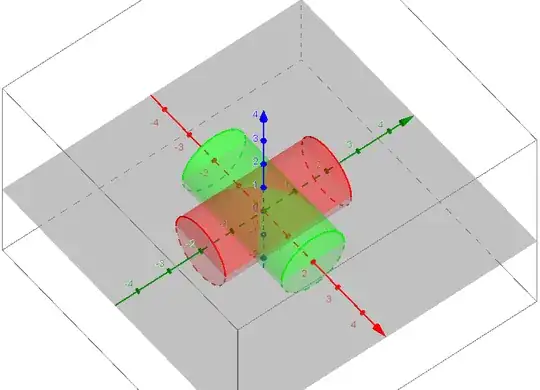
$$0\le x^2 + z^2 \le 1$$

$$0 \le y^2 + z^2 \le 1$$

I want to compute the volume of the intersection.

Sketching it out on paper is sort of nice: I see cross-sections that are disks, the first cylinder, the y-coordinate is free to vary, and for the second cylinder, the x-coordinate is free to vary.

The intersection, I would guess, seems to be something spherical.

So how can I pin down the actual set of points?

Well, one thing I thought of was to try to manipulate both inequalities to make use of the equation of a sphere, so I try looking at these inequalities instead:

$$y^2\le x^2 + y^2 + z^2 \le 1 +y^2$$

$$x^2 \le x^2 +y^2 + z^2 \le 1+x^2$$

Am I heading in the right direction? Where can I go from here?

Thanks,

user301446
  • 177

2 Answers2

9

I could not resist to model this in GeoGebra.

Steinmetz solid

Zenith is $(0, 0, 1)$ and nadir $(0, 0, -1)$. A slice at height $z$ is a square with side length $$ a = 2 \sqrt{1-z^2} $$ so $$ dV = (2 \sqrt{1-z^2})^2 dz = 4(1-z^2) dz $$ slices

mvw
  • 35,114
  • haha...@mvw, thanks so much. I am practicing for exams, so I think I had better pin down the algebra on paper for now. Hmm...so the intersection is indeed not spherical, as Professor Grant points out in his comment above... – user301446 Dec 29 '15 at 00:11
  • I hoped its surface intersection operation could deal with this one, but that is either too much yet for GeoGebra or I am doing something wrong. – mvw Dec 29 '15 at 00:14
7

The intersection of two cylinders is called a Steinmetz solid. You can give a description of the edges of the solid by

$$x = \pm z, \quad y = \pm \sqrt{1 - z^2}$$

and use these to give corresponding inequalities.

  • Hi @user, thanks so much for your quick response. Well, using the above inequalities, I do see these coming out: $x = +/- \sqrt{1-z^2}$ and $y = +/- \sqrt{1-z^2}$. How come you don't mention this guy: $x = +/- \sqrt{1-z^2}$? ... is it already like implied somewhere in your description? Thanks, – user301446 Dec 28 '15 at 23:59
  • Ooh @user, I think I see what you are saying ... – user301446 Dec 29 '15 at 00:00
  • So my above comment, I have basically found my integration limits for both x and y...is that correct, @user? And now, I just have to find the integration limits for $z$ ... – user301446 Dec 29 '15 at 00:01
  • But, solving for $z$ in each inequality gives us two upper and lower limits of integration, which is strange, @user ... – user301446 Dec 29 '15 at 00:03
  • Perhaps the limits for $z$ is simply +/- 1, since the cross-sections are disks of radius 1, @user ... what do you think? Thanks, – user301446 Dec 29 '15 at 00:06
  • Steinmetz is the German word for stone mason by the way. – mvw Dec 29 '15 at 00:12
  • Ooh, I got the right answer, @user :-) Thanks again for the helpful discussion :-) – user301446 Dec 29 '15 at 00:37
  • @user301446 Sorry - unfortunately my power went out rather couple minutes after I posted (I love winter). It seems you got everything worked out, though. –  Dec 29 '15 at 03:05
  • oh, no worries at all. Yeap, I think I got it; thanks again :-) – user301446 Dec 29 '15 at 03:11
  • And stay warm @user :-) – user301446 Dec 29 '15 at 03:11
  • Please note the Wolfram's illustration is a bit misleading: in the first pair of pictures the right solid's orientation corresponds to two 'horizontal' cylinders crossing, not a vertical with a horizontal one, as depicted on the left image. – CiaPan Dec 29 '15 at 08:48