3

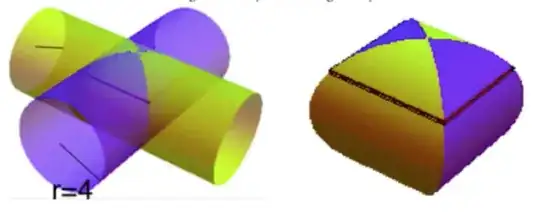
Consider two intersecting cylinders. I know the regular way to do this is:

$$ \int_{-1}^{1} \left(2\sqrt{1-2x^2}\right)^2\,dx = \frac{16}{3} $$

This methods integrates the square sides of the solid that you get

The solid described

However, is it just as viable to flip the picture 90° (have the yellow tube going up) and trying to integrate then? You will get discs where the front and back are circular but the interior is square (integrate along the yellow face on the right side image) e.g.

$$ \int_{-1}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} 2\sqrt{1-y^2}\,dy\,dx $$

Should these two integrals be equal or am I doing something wrong?

metamorphy
  • 43,591
swedishfished
  • 413

1 Answers1

1

Yes absolutely, these integrals should be equal.

However, the way you wrote it, the computation is not straightforward. Instead, note that by switching the order of the variables in the integral, it also equals $$ \int_{-1}^{1} \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} 2 \sqrt{1-y^2}\; dx dy = \int_{-1}^{1}4 (1-y^2)\; dy = \frac{16}{3} $$

Kuifje
  • 9,802
  • Could you explain the switching of the variables? – swedishfished Mar 30 '17 at 15:13
  • This volume is known as the Steinmetz solid (http://mathworld.wolfram.com/SteinmetzSolid.html) – Jean Marie Mar 30 '17 at 15:13
  • @swedishfished: you are basically integrating on a disc with radius $1$, so you can either have $-1\le x \le 1$ and $- \sqrt{1-x^2} \le y \le \sqrt{1-x^2} $ or the other way around: $-1\le y \le 1$ and $- \sqrt{1-y^2} \le x \le \sqrt{1-y^2} $ – Kuifje Mar 30 '17 at 15:15