What is the easiest way to find the area of the surface created when the cylinder $$x^2+z^2=1\text { intersects the cylinder }y^2+z^2=1.$$
I have used double integrals and also line integrals to find the area of the surface created when the cylinder $x^2+z^2=1$ intersects $ y^2+z^2=1.$
The line integral is much easier than the double integral. Is there a way to find this surface area without using integrals?
\begin{align} R &= \{ 0<x<1,-x<y<x,z=\sqrt{1-x^2} \} \\ S &= 8\iint_R dA \\ z &= \sqrt{1-x^2} \\ z_x &= -\frac{x}{\sqrt{1-x^2}} \\ z_y &= 0 \\ dA &= \sqrt{1+z_x^2+z_y^2} \, dx \, dy \\ &= \frac{1}{\sqrt{1-x^2}} \, dx \, dy \\ S &= 8\int_{0}^{1} \int_{-x}^{x} \frac{1}{\sqrt{1-x^2}} \, dy \, dx \\ S &= 8\int_{0}^{1} \frac{2x}{\sqrt{1-x^2}} \, dx \\ &= 16 \end{align}
See also ancient Chinese work, Nine Chapters《九章算術》commented by Liu Hui(劉徽) here.
Addendum
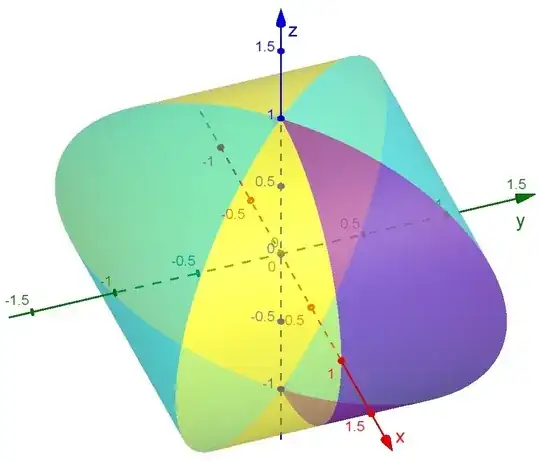In the figure above, the intersections between two cylinders (yellow and cyan) are two ellipses, namely $$x^2=y^2=1-z^2$$
Consider the purple region $T=\{ 0<y<x<1,x=\sqrt{1-z^2} \}$ which is bounded by a semi-circle in $xz$-plane and a semi-ellipse namely
$$(x,y,z)=(\sin \theta,\sin \theta,\cos \theta)$$
Now unwrapping the cylinder, $$s=\theta \implies y=\sin s$$ therefore we get a sine curve (green).
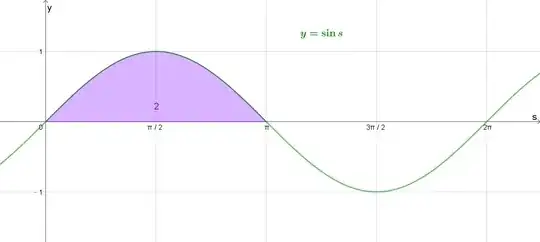
The area of purple region $T$ is
$$\int_0^\pi \sin \theta \, d\theta=2$$
which is $\dfrac{1}{8}$ of the total surface area.
