Find volume of crossed cylinders without calculus.

Question

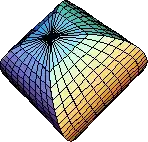
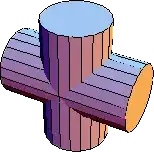
I found this puzzle here. (It's labeled "crossed cylinders".) Here's the description:

Two cylinders of equal radius are intersected at right angles as shown at left. Find the volume of the intersection between the two cylinders, without using calculus! A 3D picture of the intersection is shown at right.

Hint (medium hint - exactly which high school formulae you need): 1) Area of circle = pi * radius2, and 2) Volume of sphere = (4/3) * pi * radius3

Note: Solved by the mathematician Archimedes (287 B.C. - 212 B.C.), waaay before calculus came around!!

Please tell me how to solve this puzzle! Is there a way to do this without setting up a Riemann sum and finding a limit, essentially evaluating an integral?

This post is chosen to be the target for duplicates for finding the volume of Steinmetz solid without using calculus. For the the calculus approach, please see this. — Lee David Chung Lin, Jan 22 '19 at 10:47

score 16 · Accepted Answer · answered Nov 15 '12 at 12:26

16

Compare the solid to a sphere of the same size. The slices of the solid are squares to the sphere's circles, so the ratio of areas is always $4/\pi$. The volumes must therefore be in the same ratio, giving $(4/\pi) \cdot (4/3)\pi r^3 = (16/3) r^3$.

answered Nov 15 '12 at 12:26

Wow, that's brilliant, thank you! – littleO Nov 15 '12 at 12:28

score 0 · Answer 2 · answered Oct 11 '19 at 16:52

Using prismoidal formula. Area at the Middle of the intersectcion is a square with sides 2r, so the area is 4r^2. Then the area at the top and bottom is 0. The length of the area of intersection is the diameter of cylinder equal to 2r.

Prismoidal formula. V= L*(Atop +4Amid + Abot)/6 V= 2r(0+4*4r^2+0)/6 =(16/3) * r^3

Find volume of crossed cylinders without calculus.

2 Answers2

Linked