Find the volume of the solid bounded by the cylinders $y=x^2, y=z^2$ and the plane $y=1$
I think the integral should be: $$\int_0^1\int_{-\sqrt y}^\sqrt y\int_{-\sqrt y}^\sqrt y\ dx\,dz\,dy$$
Could someone tell me if this is correct?
Asked
Active
Viewed 1,006 times
1
-
1Would your integral have been any different for $y=x^4$ and $y=z^4$? – hmakholm left over Monica Dec 16 '13 at 04:16
-
@HenningMakholm I made a typo on the integral limits. Should have been $-\sqrt y , to \sqrt y$. Is it correct now? – EggHead Dec 16 '13 at 12:46
-
@user116056 Corrected my typo on the integral limits. Is it correct now? – EggHead Dec 16 '13 at 12:48
-
That looks more like it -- though using a double integral to calculate the area of a square with known side length is rather overkill ... – hmakholm left over Monica Dec 16 '13 at 12:50
1 Answers
1
This is not quite right. The region of integration there is not curved but straight like this:
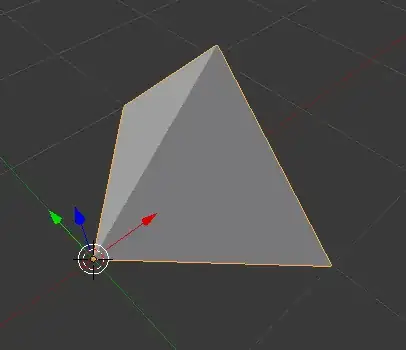
Instead, maybe to
use cylindrical coordinates.
Also please look at this question here: Find the volume common to two circular cylinders, each with radius r, if the axes of the cylinders intersect at right angles. (using disk/washer).
user116056
- 41