If $(a,b,c)$ are the sides of a triangle, what is the probability that $ac>b^2$?

Question

Let $a \le b \le c$ be the sides of a triangle inscribed inside a fixed circle such that the vertices of the triangle are distributed uniformly on the circumference.

Question 1: Is it true that the probability that $ac > b^2$ is $\displaystyle \frac{1}{5}$. I ran a simulation by generating $1.75 \times 10^9$ triangle and counting the number of times $ac > b^2$. The experimental data seems to suggest that probability converges to about $0.2$.

Note: For any triangle with $a \le b \le c$, the triangle inequality implies $b < a+c < 3b$. Now the condition $ac > b^2$ implies that $2b < a+c < 3b$; here the lower bound follows from AM-GM inequality. Hence all triangles for which $b < a+c < 2b$ are ruled out. For our problem, the condition $2b < a+c < 3b$ is necessary but not sufficient.

Update: Changed the title in light of the comments and answer that relaxing the condition $a\le b \le c$ is easier to handle

Related question: If $(a,b,c)$ are the sides of a triangle and $x \ge 1$, what is the probability that $a+b > cx$?

Answer 1

Assume that the circle is the unit circle centred at the origin, and the vertices of the triangle are:
$A(\cos(-Y),\sin(-Y))$ where $0\le Y\le2\pi$
$B(1,0)$
$C(\cos X,\sin X)$ where $0\le X\le2\pi$

Relax the requirement that $a \le b \le c$, and let:
$a=BC=2\sin\left(\frac{X}{2}\right)$
$b=AC=\left|2\sin\left(\frac{2\pi-X-Y}{2}\right)\right|=\left|2\sin\left(\frac{X+Y}{2}\right)\right|$
$c=AB=2\sin\left(\frac{Y}{2}\right)$

$\therefore P[ac>b^2]=P\left[\sin\left(\frac{X}{2}\right)\sin\left(\frac{Y}{2}\right)>\sin^2\left(\frac{X+Y}{2}\right)\right]$ where $0\le X\le2\pi$ and $0\le Y\le2\pi$

This probability is the ratio of the area of the shaded region to the area of the square in the graph below.

Rotate these regions $45^\circ$ clockwise about the origin, then shrink by factor $\frac{1}{\sqrt2}$, then translate left $\pi$ units, by letting $X=x+\pi-y$ and $Y=x+\pi+y$.

$\begin{align} P[ac>b^2]&=P\left[\sin\left(\frac{x+\pi-y}{2}\right)\sin\left(\frac{x+\pi+y}{2}\right)>\sin^2(x+\pi)\right]\\ &=P\left[\cos(x+\pi)-\cos y<-2\sin^2(x+\pi)\right]\text{ using sum to product identity}\\ &=P\left[-\cos x-\cos y<-2\sin^2 x\right]\\ &=P\left[-\arccos(2\sin^2x-\cos x)<y<\arccos(2\sin^2x-\cos x)\right]\\ &=\dfrac{\int_0^{\pi/3}\arccos(2\sin^2x-\cos x)\mathrm dx}{\frac{\pi^2}{2}} \end{align}$

Numerical evidence suggests that the integral equals $\frac{\pi^2}{5}$. (I've posted this integral as another question.) If that's true, then the probability is $\frac25$.

If the probability without requiring $a \le b \le c$ is $\frac25$ , it follows that the probability with requiring $a \le b \le c$ is $\frac15$, as @joriki explained in the comments.

Update:

The integral has been shown to equal $\frac{\pi^2}{5}$, thus showing that the answer to the OP is indeed $1/5$.

The simplicity of the answer, $1/5$, suggests that there might be a more intuitive solution, but given the amount of attention the OP has received, an intuitive solution seems to be quite elusive. We might have to chalk this one up as another probability question with a simple answer but no intuitive explanation. (Other examples of such probability questions are here and here.)

Answer 2

This is not an answer, rather a numerical exploration. We may suppose that the three points are on the unit circle and that one of them is $P=(1, 0)$. Let the two other points be $Q = (\cos x, \sin x)$ and $R=(\cos y, \sin y)$. Let us define the set \begin{equation} S = \{(x, y) | \min(a,b,c)\max(a,b,c)> \text{mid}(a,b,c)^2\} \end{equation} where $a = 2 |\sin(x/2)|$, $b = 2|\sin(y/2)|$, $c = 2|\sin((x-y)/2)|$ are the lengths of the sides of the triangle.

I was able to plot the indicator function ${\bf 1}_S(x,y)$ in The picture of ${\bf 1}_S(x+\frac{y}{2},y)$ shows even more regularity. It seems that only a few sine-like curves are involved in this picture

Edit: I updated the pictures. The original version of this post inverted the $x$ and $y$ axis.

Using @joriki 's comment that the problem is equivalent to showing that the probability of the unordered triple $(a, b, c)$ satisfies $a c > b^2$ is $2/5$ allows us to create a simpler picture. Let \begin{equation} U = \{(x, y) | a c> b^2\} \end{equation} with the same definition of $a, b, c$. Plotting the function ${\bf 1}_U(x+\frac{y}{2},y)$ gives the much simpler picture

The sine-looking function appearing in this picture can be proved to have the equation \begin{equation} y = 2 \arccos\left(-\frac{1}{4} + \frac{1}{4}\sqrt{17 + 8\cos x}\right) \end{equation} for $0\le x\le \pi$. So the question reduces to: Is is true that \begin{equation} \frac{2}{\pi^2} \int_0^\pi \arccos\left(-\frac{1}{4} + \frac{1}{4}\sqrt{17 + 8\cos x}\right) d x = \frac{2}{5} \end{equation} WolframAlpha actually gives this value numerically. Here is how the equation of the curve can be established, recall that $2 \sin u \sin v = \cos \left(u-v\right)-\cos \left(u+v\right)$, then

\begin{equation}\renewcommand{\arraystretch}{1.5} \begin{array}{rl}&\sin \left(\frac{x}{2}+\frac{y}{4}\right) \sin \left(\frac{x}{2}-\frac{y}{4}\right) = {\sin }^{2} \left(\frac{y}{2}\right)\\ \Longleftrightarrow &\displaystyle \frac{1}{2} \left(\cos \left(\frac{y}{2}\right)-\cos \left(x\right)\right) = {\sin }^{2} \left(\frac{y}{2}\right)\\ \Longleftrightarrow &\displaystyle {\cos }^{2} \left(\frac{y}{2}\right)+\frac{1}{2} \cos \left(\frac{y}{2}\right)-\left(1+\frac{\cos \left(x\right)}{2}\right) = 0\\ \Longleftrightarrow &\displaystyle \cos \left(\frac{y}{2}\right) =-\frac{1}{4} \pm \frac{1}{4} \sqrt{17+8 \cos \left(x\right)}\\ \Longleftrightarrow &\displaystyle \cos \left(\frac{y}{2}\right) =-\frac{1}{4} + \frac{1}{4} \sqrt{17+8 \cos \left(x\right)} \end{array}\end{equation}

Answer 3

Let $0\lt x\le y\le z\lt\pi$ be the three half-angles of the triangle, with $x+y+z=\pi$. Then with the comment by @Gribouillis the condition $ac\gt b^2$ translates to

$$ \sin x\sin z\gt\sin^2y $$

and thus, with $\sin z=\sin(\pi-x-y)=\sin(x+y)$, to

$$ \sin x\sin(x+y)\gt\sin^2 y\;. $$

Applying the addition theorem yields

$$ \sin x(\sin x\cos y+\cos x\sin y)\gt\sin^2y\;. $$

To solve for $x$, isolate $\cos x$,

$$ \cos x\gt\frac{\sin y}{\sin x}-\frac{\sin x}{\sin y}\cos y\;, $$

square,

$$ \cos^2 x\gt\frac{\sin^2 y}{\sin^2 x}+\frac{\sin^2 x}{\sin^2 y}\cos^2y-2\cos y\;, $$

use $\sin^2x+\cos^2x=1$ and $\sin^2y+\cos^2y=1$ and simplify:

$$ 1+2\cos y\gt\frac{\sin^2 y}{\sin^2 x}+\frac{\sin^2 x}{\sin^2 y}\;. $$

This is a quadratic inequality for $\frac{\sin^2 x}{\sin^2 y}$, and the relevant solution branch in our case is

$$ \frac{\sin^2 x}{\sin^2 y}\gt\frac12+\cos y-\sqrt{\left(\frac12+\cos y\right)^2-1}\;. $$

Thus the bound for $x$ as a function of $y$ is

$$ x\gt f(y):=\arcsin\left(\sin y\sqrt{\frac12+\cos y-\sqrt{\left(\frac12+\cos y\right)^2-1}}\right)\;. $$

The range for $x$ is $0\lt x\le y$ if $y\le\frac\pi3$ and $0\lt x\le1-2y$ if $\frac\pi3\le y\lt\frac\pi2$. In the latter case, we never have $ac\gt b^2$, so the desired probability is

\begin{eqnarray*} 1-\frac{\int_0^\frac\pi3f(y)\mathrm dy+\int_\frac\pi3^\frac\pi2(1-2y)\mathrm dy}{\int_0^\frac\pi3y\mathrm dy+\int_\frac\pi3^\frac\pi2(1-2y)\mathrm dy} &=& 1-\frac{\int_0^\frac\pi3f(y)\mathrm dy+\frac{\pi^2}{36}}{\frac{\pi^2}{18}+\frac{\pi^2}{36}} \\ &=&\frac23-\frac{12}{\pi^2}\int_0^\frac\pi3f(y)\mathrm dy\;. \end{eqnarray*}

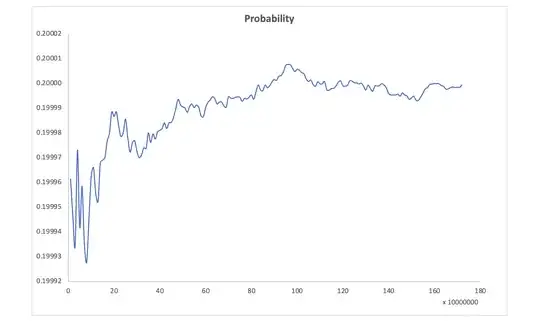
This is $\frac15$ if we have

\begin{eqnarray*} \int_0^\frac\pi3f(y)\mathrm dy &=& \frac7{180}\pi^2 \\ &\approx& 0.383817948931253\;, \end{eqnarray*}

and indeed this is what a numerical Wolfram|Alpha integration to $15$ decimal places yields.

I haven’t been able to solve the integral analytically, but in any case, this is a very inelegant approach – a simple result like $\frac15$ for a geometric probability usually has a nice explanation based on symmetry. I was hoping that perhaps one could show that exactly $2$ of the $10$ triangles formed by $5$ points fulfil the condition, but this is far from the case; that number varies between $0$ and $5$. Still, I wouldn’t be surprised if someone comes up with an elegant solution.

Answer 4

Let the fixed circle be of unit radius and center $(0,0)$ and define the vertices of the triangle as: $$ B=(1,0),\quad C=(\cos\gamma,\sin\gamma),\quad A=(\cos\alpha,\sin\alpha), $$ where $\gamma=\angle BOC <\alpha =\angle BOA$. Define as usual: $$ a=BC,\quad b=AC,\quad c=AB. $$ The condition $b\ge a$ is equivalent to ${1\over2}(\alpha-\gamma)\ge{1\over2}\gamma$, that is: $\alpha\ge2\gamma$. The condition $c\ge b$ is equivalent to $\pi-{1\over2}\alpha\ge{1\over2}(\alpha-\gamma)$, that is: $\alpha\le\pi+{1\over2}\gamma$. These inequalities can be rewritten as: $$ 0\le\gamma\le{2\over3}\pi,\quad 2\gamma\le\alpha\le\pi+{1\over2}\gamma. $$ The condition $ac>b^2$ can be written as $$ \sin{\alpha\over2}\sin{\gamma\over2}>\sin^2{\alpha-\gamma\over2} $$ but explicitating from that some bounds for $\alpha$ and $\gamma$ is very difficult. Anyway, the requested probability $p$ can be computed from: $$ p={\int_0^{2\pi/3}\int_{2\gamma}^{\pi+\gamma/2}I(\alpha,\gamma)\,d\alpha d\gamma \over \int_0^{2\pi/3}\int_{2\gamma}^{\pi+\gamma/2}d\alpha d\gamma}, $$ where $$ I(\alpha,\gamma)=\cases{ 1 & if $\sin{\alpha\over2}\sin{\gamma\over2}>\sin^2{\alpha-\gamma\over2}$\\ 0 & otherwise } $$ I computed that numerically and got $p\approx0.20000$, with Mathematica complaining that the estimate of the error was $\approx0.00004$. Playing with the options in Mathematica, or using some other tool, might lead to more accurate results.

Answer 5

Too long for a comment :

The problem of the order fixing the value of the probability can be solved using the concept of duality ( the dual of a triangle is also a triangle)

Next we have a useful formula see the wiki page Crofton formula

I quote a part of it :

$S_1$,$S_2$, with $S_{1}$ nested inside $S_{2}$, the probability of a random line $l$ intersecting the inner surface $S_{1}$,conditional on it intersecting the outer surface , is...

End of the quote

So in this case we start by the integral defining the probability in term of area and to conclude we use the condition $ac>b^2$

Further explanation :

If we take two triangle one in another the probability that a line intersecting the two triangle (given above) is equivalent to says excluding the homothetic case that one of the side is sufficiently large and so there is a constraint on it or here $ac>b^2$