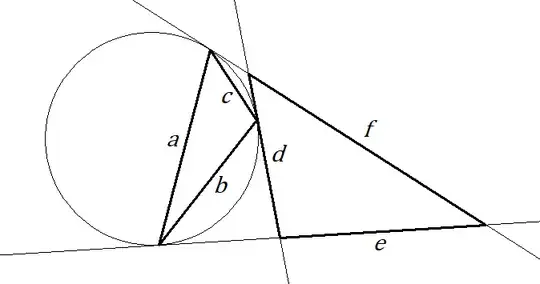
On a circle, choose three uniformly random points $A,B,C$.
Triangle $T_1$ has vertices $A,B,C$. The side lengths of $T_1$ are, in random order, $a,b,c$.
Triangle $T_2$ is formed by drawing tangents to the circle at $A,B,C$. ($T_2$ may or may not lie inside the circle.) The side lengths of $T_2$ are, in random order, $d,e,f$.
Is the following conjecture true:
The distribution of ratios of $a,b,c$ is the same as the distribution of ratios of $d,e,f$.
So for example, if my conjecture is true, then we would have the following probability equations:
- $P(a^2+b^2<c^2)=P(d^2+e^2<f^2)$
- $P(a^3+b^3<c^3)=P(d^3+e^3<f^3)$
- $P(ab<c^2)=P(de<f^2)$
- $P\left(\frac1a+\frac1b<\frac1c\right)=P\left(\frac1d+\frac1e<\frac1f\right)$
(My conjecture, if true, would not imply that $P(ab<c)=P(de<f)$, because these inequalities are not dimensionally homogeneous.)
Basis for my conjecture
I found that $P(ab<c^2)=\frac35$. Then I wondered what $P(de<f^2)$ equals, and a simulation suggests that it also equals $\frac35$.
I found that $P\left(\frac1a+\frac1b<\frac1c\right)=\frac15$. Then I wondered what $P\left(\frac1d+\frac1e<\frac1f\right)$ equals, and a simulation suggests that it also equals $\frac15$.
I tried some other probabilities, and simulations suggest that each probability has the same value for the two triangles.
So I suspect that the two triangles have the same distribution of ratios of side lengths. But I don't know why.