Graph Transformation

Question

Knowing dealing with graph transformations come handy MANY times.
I searched on google to get a comprehensive graph transformation list but couldn't find one. Some good while back I learned them all with great enthusiasm but have now all forgotten them and like before, I'm not finding a great teacher neither a great search result. Can we have one here that will cover the following (at least):

$$\text {For }y=f(x):$$ $y=f(x+c)$
$y=f(x)+c$
$y=f(cx)$
$y=cf(x)$
$y=f(-x)$
$y=-f(x)$
$y=f(|x|)$
$y=|f(x)|$
$y+c=f(x)$
$cy=f(x)$
$-y=f(x)$
$|y|=f(x)$

Kindly feel to provide for more in case I have missed out any thing. Thank you :)

---

Note: Last few equations I know might be a repeat of the above cases but I have included them so as to clear any confusions.

Answer 1

\begin{array}{|c|c|c|c|} \hline \text{New function}(c>0,\lambda>1)& \text{Change of coordinate}& \text{Geometry of transformation} \\ \hline f(x) +c & (a, b) \mapsto(a,b+c)& \text{ shift up by} c\\ \hline f(x) -c & (a, b) \mapsto(a,b-c)&\text{shift down by} c\\ \hline \lambda f(x) & (a, b) \mapsto(a,\lambda b)&\text{vertical expansion by } \lambda\\ \hline \frac{1}{\lambda}f(x) & (a, b) \mapsto(a, \frac{1}{\lambda}b)&\text{vertical contraction by } \lambda \\\hline -f(x) &(a, b) \mapsto (a, -b) &\text{reflexion about $x$-axis}\\ \hline \end{array}

---

Example:

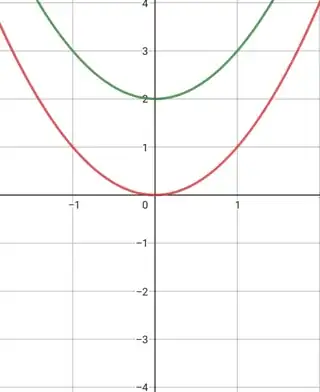
$\boxed{\color{red}{f(x) =x^2}}$

$\boxed{\color{green}{f(x) =x^2+2}}(\text{ shifted upward $2$ units}) $

$\boxed{\color{black}{f(x)=x^2-2}}(\text{ shifted downward $2$ units}) $

$\boxed{\color{goldenrod}{f(x) =3x^2}}(\text{ vertically expanded $3$ units}) $

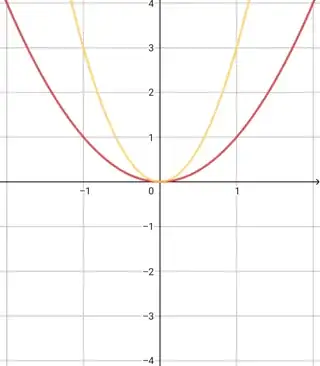
$\boxed{\color{blue}{f(x) =\frac{1}{3}x^2}} (\text{vertically contracted $\frac{1}{3}$ units}) $

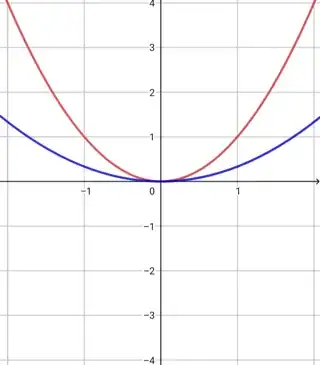
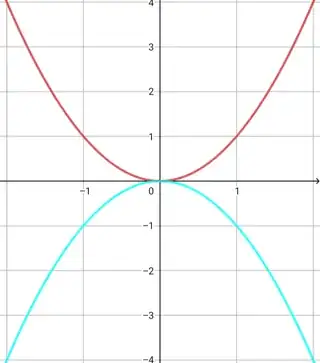
$\boxed{\color{cyan}{f(x) =-x^2}} (\text{reflected about $x$- axis}) $

---

---

\begin{array}{|c|c|c|c|} \hline \text{New function}(c>0,\lambda>1)& \text{Change of coordinate}& \text{Geometry of transformation} \\ \hline f(x+c) & (a, b) \mapsto(a-c,b)& \text{ shift left by} c\\ \hline f(x-c) & (a, b) \mapsto(a+c,b)&\text{shift right by} c\\ \hline f(\lambda x) & (a, b) \mapsto(\frac{1}{\lambda}a,b)&\text{horizontal contraction by } \frac{1}{\lambda} \\ \hline f(\frac{1}{\lambda}x) & (a, b) \mapsto(\lambda a,b)&\text{horizontal expansion by } \lambda \\\hline f(-x) &(a, b) \mapsto (-a, b) &\text{reflexion about $y$-axis}\\\hline \end{array}

---

Example:

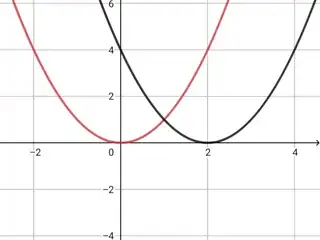
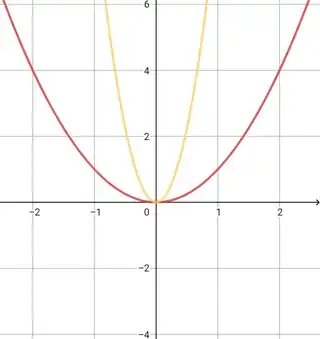
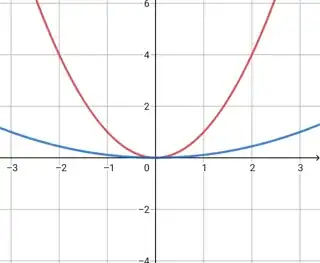
$\boxed{\color{red}{f(x) =x^2}}$

$\boxed{\color{green}{f(x) =(x+2)^2}}(\text{ shifted left $2$ units}) $

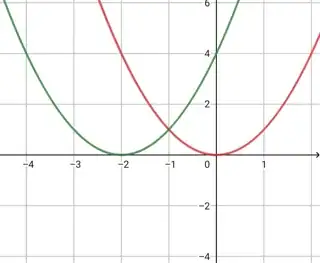
$\boxed{\color{black}{f(x)=(x-2)^2}}(\text{ shifted right $2$ units}) $

$\boxed{\color{goldenrod}{f(x) =(3x)^2}}(\text{horizontally contracted $\frac{1}{3}$ units})$

$\boxed{\color{blue}{f(x) =(\frac{1}{3}x)^2}} (\text{horizontally expanded ${3}$ units}) $

$\boxed{\color{cyan}{f(x) =(-x) ^2}} (\text{reflected about $y$- axis}) $

---

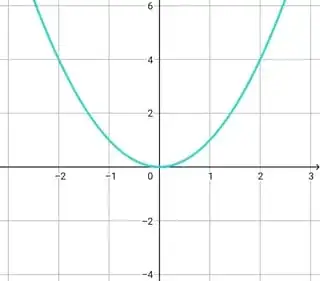
$|f|=|\space |\circ f$

$|f(x)| =\begin{cases}f(x)& f(x) \ge 0\\-f(x)& f(x) <0\end{cases}$

Hence $|f|$ is same as $f$ on the upper half plane and the lower half plane $f$ is $-f$ .

In other words $|f|=\max\{f, -f\}$

To draw the graph of $|f|$ , first draw the graph of $f$ and the leave the portion of the graph as it is on the upper half plane and then reflect the portion of the graph of the lower half plane with respect to the $x$-axis.

---

$f(|x|) =(f\circ|\space |)(x) $

$f(|x|) =\begin{cases}f(x)& x\ge 0\\f(-x) & x <0\end{cases}$

Hence $f(|x|)$ is same as $f(x)$ on the right half plane and on the left half plane $f(|x|)$ is the reflection of $f(x)$ about $y$-axis.

To draw the graph of $f\circ |x|$ , first draw the graph of $f$ and the leave the portion of the graph as it is on the right half plane and then reflect the portion of the graph in the left half plane with respect to the $y$-axis.

Note: For a even function $f$, since $f(-x) =f(x) $ then $f(|x|) =f(x) $.Hence we won't see the difference between the graph of the function $f$ and $f\circ |\space |$.

---

Example:

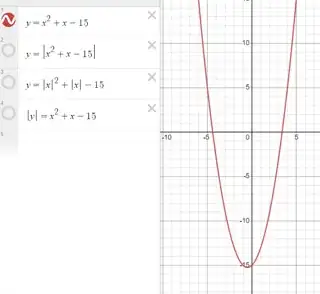
$\boxed{\color{red}{f(x) =-x^3}}$

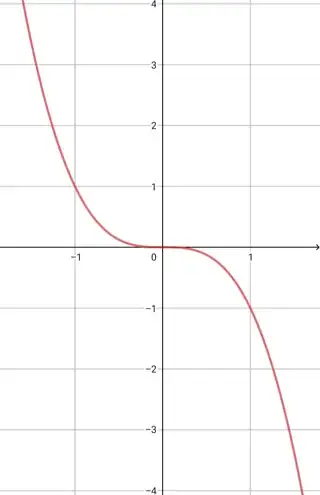
$\boxed{\color{blue}{|f(x)| =|-x^3|}}$

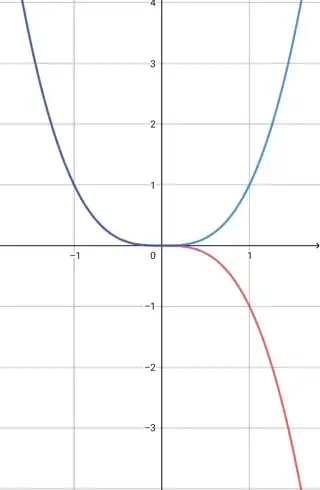
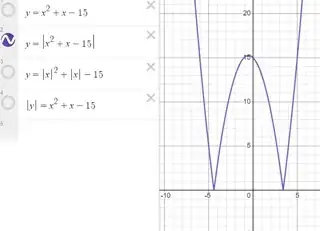
$\boxed{\color{green}{|f(x)| =-|x|^3}}$

---

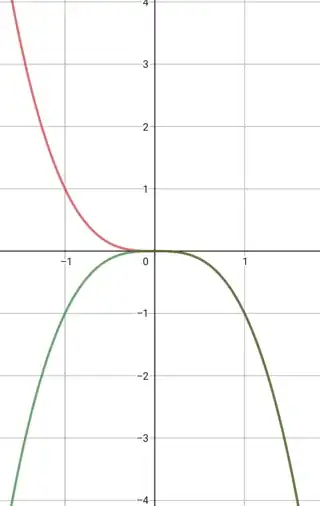
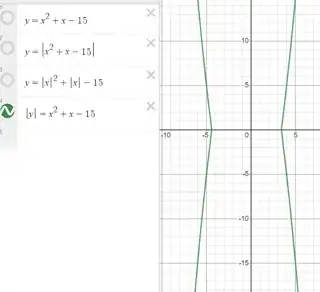
$\boxed{\color{black}{|y|=f(x)}}$

$y =\begin{cases}f(x)& y\ge 0\\-f(x) & y <0\end{cases}$

Hence the graph of the function $|y|=f(x) $ is same as the graph of $y=f(x)$ on the upper half plane and on the lower half plane the graph of $|y|=f(x) $ is same as the graph of $y=-f(x) $.

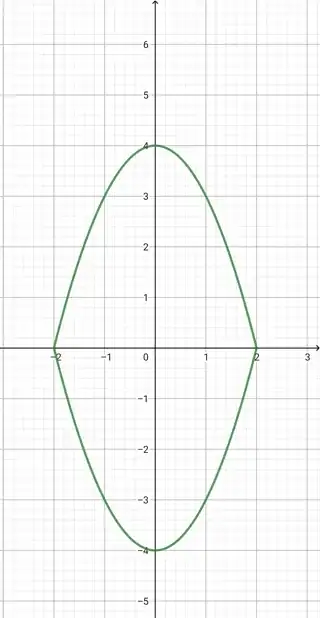
To draw the graph of $|y|=f(x) $, first draw the graph of $y=f(x)$.Then left the graph on the upper half plane as it is and then reflect the graph of the upper half plane about $x$-axis.

Example:

$\boxed{\color{red}{f(x) =4-x^2}}$

The graph of $y=f(x)$

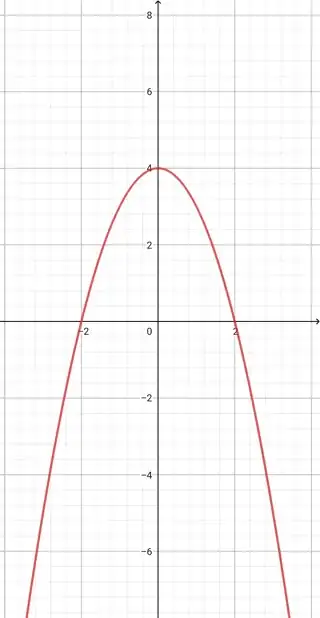
$\boxed{\color{green}{|y|=f(x)}}$

---

Answer 2

$y = f(x+c)$ translates the graph by $-c$ in the x direction.

$y = f(x) + c$ translates the graph by $c$ in the y direction.

$y = f(cx)$ stretches the graph by a factor of $\frac{1}{c} $ in the x direction.

$y = cf(x)$ stretches the graph by a factor of $c$ in the y direction.

$y = f(-x)$ reflects the graph in the y axis.

$y = -f(x)$ reflects the graph in the x axis.

$y = f(|x|)$ keeps the positive x axis side the same, but the negative side becomes a reflection of the positive side.

$y = |f(x)|$ keeps the positive y values all the same, but the negative parts are now reflected in the x axis.

$y + c = f(x)$ translates the graph by $-c$ in the y direction.

$cy = f(x)$ stretches the graph by a factor of $\frac{1}{c}$ in the y direction.

$-y = f(x)$ is the same as $y = -f(x)$ above.

$|y| = f(x)$ keeps the positive y axis side the same, and the negative y axis side is now a reflection of the positive side.

Hopefully these explanations are clear and intuitive.

Answer 3

1. Given the graph of $y=f(x),$ perhaps think of the output modifications $$y=af(x)\\y=f(x)+b$$ as (vertical) transformations of the curve, whereas the input modifications $$y=f(ax)\\y=f(x+b)$$ as (horizontal) transformations of the coordinate axes.

   This is just so that we can continue to naturally think of addition as a shift in the positive (rather than negative) direction, and multiplication by a number greater than $1$ as an enlargement (rather than a reduction).

2. So, to transform the graph of $y=f(x)$ to that of $y=f(3x-21),$ noting that $$f((3x)-21)\equiv f(3(x-7)),$$ we can either

   • translate the $x$-axis $21$ units leftward then scale it by a factor of $3$

   or

   • scale the $x$-axis by a factor of $3$ then translate it $7$ units leftward.

3. • $y=|f(x)|$ reflects across the $x$-axis any negative-$y$ portion of the curve.

   • $y=f(|x|)$ deletes any negative-$x$ portion of the curve, then duplicates the remaining curve by reflecting it across the $y$-axis.

   • $|y|=f(x)$ deletes any negative-$y$ portion of the curve, then duplicates the remaining curve by reflecting it across the $x$-axis.