1

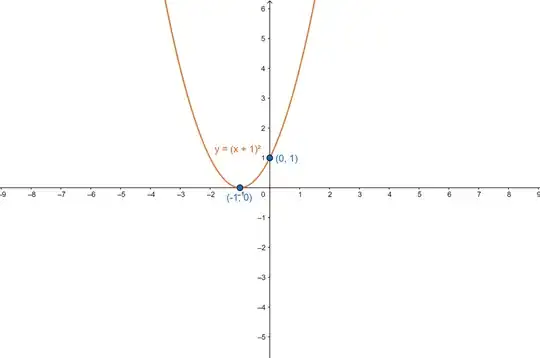
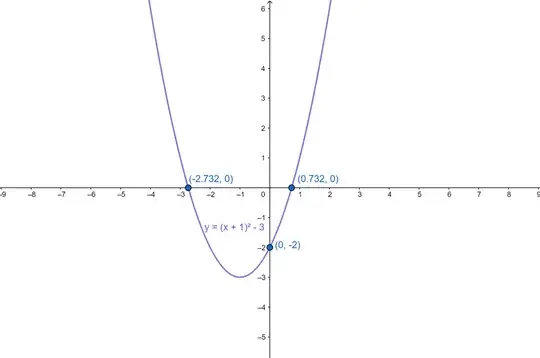
Question:

Sketch the graph of $ y=(x+1)^{2}-3 $ show the curve intersects the $x$ and $y$ axis

So for the $y$-intercept I calculated this to be $-2$.

However, for the $x$-intercept do you compute using completing the square or expanding the brackets and then deriving the quadratic formula?

Peter Phipps
  • 3,100
AMN
  • 161
  • 7
  • Why must you use a formula to find the $x$-intercepts? Calculate them the same way you calculated the $y$-intercept. – Andrew Chin Aug 24 '22 at 17:51
  • 1
    For x interceps set $y=0$ and solve. In your case that can be done with a few manipulations, no need for quadratic equation [the square is almost already completed.] – coffeemath Aug 24 '22 at 17:53
  • I had assumed due to the way function and how completing the square is set out you use it+ i try to go for the fastest method possible on my calculator @AndrewChin – AMN Aug 24 '22 at 17:59
  • So when y=0 0=(x+1)^2-3? @coffeemath and then x is either + or negative root 3 or -1 positive or neagtive root 3? – AMN Aug 24 '22 at 18:02
  • 1
    See here – SoG Aug 24 '22 at 18:03
  • AMN--- not quite. One gets $(x+1)^2=3$ so that $x+1=\pm \sqrt{3}.$ Finally subtract $1$ from eacjh side get $x=-1 \pm \sqrt{3}.$ – coffeemath Aug 24 '22 at 19:28

2 Answers2

3

You may also use Graph Transformations.
The best thing about it is that if you know the basic graph, you may easily arrive at your desired graph.
Here's how you'd do it: $$y=x^2$$ enter image description here $$y=(x+1)^2$$ enter image description here $$y=(x+1)^2-3$$ enter image description here

To get the value of intercepts, put $x=0$ and then $y=0$ in your equation to get respectively the values for x-intercept and y-intercept.

$x$-intercept:
$y=(0+1)^2-3=-2$
$x$-intercept$=(0,-2)$

$y$-intercept:
$0=(x+1)^2-3$
$\pm\sqrt3=x+1$
$\Rightarrow x=-1\pm\sqrt3$
$y$-intercept$=(-1+\sqrt3)$ and $(-1-\sqrt3)$

VoidGawd
  • 3,110
0

The curve is shown in the link by the User pips.
The curve crosses the $y$-axis at $x=0$, i.e. $y=-2$ and it crosses the $x$-axis, known as the roots of the quadratic (polynomial) equation at $y=0$, i.e. $x=\sqrt3 -1$ and at $-1-\sqrt3$.

VoidGawd
  • 3,110
Amoolya Prasad
  • 35