Graph of $|x+y|+|x-y|=2$ using graph transformations?

Question

Question:

How to draw the following graph? $$|x+y|+|x-y|=2$$

I came across this question while doing the topic "Graph Transformation". The link contains all the transformations I know.

My approach:

I took $k=x+y$ and $l=x-y$ to get $|k|+|l|=2$ but I got too confused in this. And I couldn't think of anything else.

How can I plot the graph using graph transformations? Please help.

Answer 1

First, plot the equation $|x|+|y| = \frac{2}{\sqrt{2}}$ by finding the four $x,y$ intercepts, and connecting them with straight lines.

The original equation is this square rotated in the plane by $\pi/4$, or 45 degress. This I think is what is meant by "transformation." (in this case, contraction followed by rotation).

Answer 2

This equation is invariant under $x\to -x, y\to -y, x\to \pm y$ it is symmetric in all quadrants and about lines $y=\pm x$. Iin the first quadrant.

Case 1: when $x>y$ we have $x=1$

Case 2: when $x <y$, then $y=1$

These two cases give a square. In first quadrant. In all quadrants we have a square with four corners $(\pm 1,\pm 1)$.

Answer 3

This exercise is an example of a much more general kind of transformation than the ones you examined in your previous question about graph transformations.

Previously, you started with the graph of a function whose equation was $y = f(x).$ You made modifications to this equation, but in all cases you had an expression in $y$ on one side of the equation and an expression in $x$ on the other side of the equation. In addition, the transformed graph was also the graph of a function except for the transformation to $\lvert y\rvert = f(x)$.

Now you are venturing into new territory. This equation has $x$ and $y$ on the same side of the equation, and it is not easy to see how to rearrange the equation to have $x$ only on one side and $y$ only on the other side.

People will often say that an equation like this is the equation of a curve rather than a function. For example, the graph of $x^2 + y^2 = 1$ is a circle, which is not the graph of a function but is a curve.

A more general way to describe this is that the equation of a curve is $$ g(x,y) = 0. $$

You can transform the graph of this equation similarly to transforming the graph of a function:

• $g(x + c, y) = 0$ moves the graph $c$ units left.
• $g(x, y + c) = 0$ moves the graph $c$ units down.
• $g(x/\lambda, y) = 0$ enlarges the graph by a factor of $\lambda$ horizontally.
• $g(x, y/\lambda) = 0$ enlarges the graph by a factor of $\lambda$ vertically.
• $g(x/\lambda, y/\lambda) = 0$ enlarges the graph by a factor of $\lambda$ both horizontally and vertically, with the result that it enlarges the graph equally in all directions.
• $g(-x, y) = 0$ replaces the graph by its own mirror image flipped left to right.
• $g(x, -y) = 0$ replaces the graph by its own mirror image flipped top to bottom.
• $g(\lvert x\rvert, y) = 0$ erases everything to the left of the $y$-axis and then copies a mirror image from the right side of the $y$-axis to the left side.
• $g(x, \lvert y\rvert) = 0$ erases everything below the $x$-axis and then copies a mirror image from the half-plane above the $x$-axis to the half-plane below.

There is another transformation that is often applied to graphs specified by this kind of equation:

• $g(x\cos\theta + y\sin\theta, -x\sin\theta + y\cos\theta) = 0$ rotates the graph of $g(x,y) = 0$ by an angle $\theta$ counterclockwise around the point $(0,0).$

This can be combined with other transformations:

• $g((x\cos\theta + y\sin\theta)/\lambda, (-x\sin\theta + y\cos\theta)/\lambda) = 0$ rotates the graph of $g(x,y) = 0$ by an angle $\theta$ counterclockwise around $(0,0)$ and enlarges it by a factor of $\lambda$ in all directions.

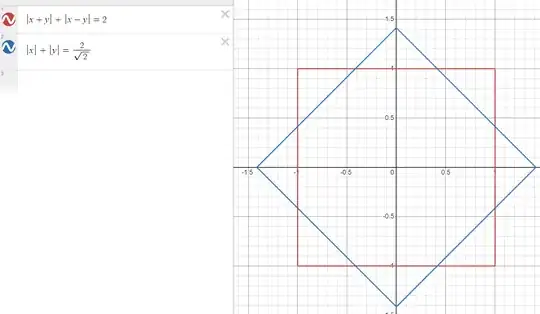
The equation you are looking at in the question can be fit into this format by setting $$g(x,y) = \lvert x+y\rvert + \lvert x-y\rvert - 2.$$

To an experienced eye, the use of $x + y$ in one place and $x - y$ in another shouts "rotation!" Partly this is because someone experienced in rotations of graphs will have seen rotations like that before.

To get the graph you are looking for, we can start by defining $ g_0(x, y) = x + y - 2. $ Then the graph of $g_0(x,y) = 0$ is the graph of $x + y = 2,$ which is a straight line that goes through $(0,2)$ on the $y$-axis and $(2,0)$ on the $x$-axis.

Next we look at the graph of $g_0(\lvert x\rvert, y) = 0.$ This discards the part of the line to the left of the $y$-axis and adds a mirror image of the right-hand side of the line. So now we have a graph that passes through $(-2,0),$ then goes straight to $(0,2),$ where it makes a $90$-degree turn and goes straight to $(2,0)$ and continues beyond.

Next we look at the graph of $g_0(\lvert x\rvert,\lvert y\rvert) = 0.$ This discards the part of the previous graph below the $x$-axis and adds a mirror image of the upper part of the graph. We end up with a square with vertices at $(-2,0),$ $(0,2),$ $(2,0),$ and $(0,-2).$ Note that the sides of the square are all at $45$-degree angles with the axes, the length of each side is $2\sqrt2,$ and the center of the square is at $(0,0).$

Finally we make the substitution \begin{align} x &\rightarrow \sqrt2(x\cos(-\tfrac\pi4) + y\sin(-\tfrac\pi4)) = x - y, \\ y &\rightarrow \sqrt2(-x\cos(-\tfrac\pi4) - y\sin(-\tfrac\pi4)) = x + y. \\ \end{align} This rotates the graph by an angle $-\tfrac\pi4$ counterclockwise, which is to say it rotates the graph $\tfrac\pi4$ (an angle of $45$ degrees) clockwise, and also enlarges the graph by a factor of $1/\sqrt2$, which is to say it shrinks the graph by a factor of $\sqrt2.$

After this substitution the equation of the graph becomes $$ g_0(\lvert x - y\rvert,\lvert x + y\rvert) = 0, $$ which is equivalent to $$ \lvert x+y\rvert + \lvert x-y\rvert = 2, $$ which is the equation you wanted to graph. So we have the desired graph now.

The rotation by $45$ degrees makes the sides of the square parallel to the axes (instead of at $45$-degree angles) and shrinking by a factor of $\sqrt 2$ reduces the lengths of the sides from $2\sqrt2$ to just $2.$ So we have a square of side $2,$ centered at $(0,0),$ with sides parallel to the axes.