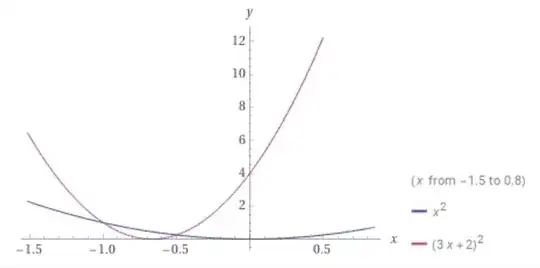
$y = x^n $ is transformed to $0.5(3x+2)^n - 1$. Describe the transformations.
Not too sure on this one, but I factorised $3x+2$ to $3(x+2/3)$, giving me a translation $-2/3$ to the left followed by a stretch scale factor $1/3$ parallel to x-axis. After that, it would be stretch scale factor $1/2$ parallel to y-axis followed by a translation 1 unit down.
This definitely doesn't seem right though. My only other thought would be to find the inverse of $3x+2$ which is $(x-2)/3$.
Cheers guys