1

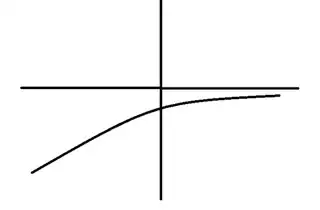
I had a question about $y=\sqrt{-x+4}$. I missed it, because I first reflected about the y axis then moved the graph left 4. That was wrong, because apparently I need to factor out a -1 to get $y=\sqrt{-1(x-4)}$, and the graph should actually shift to the right, instead of left.

Then I had $y=-2(3)^{5-x}$. Following the logic of the previous problem, I would factor out a -1 to get $y=-2(3)^{-1(-5+x)}$, and shift the graph to the right. However, this is not correct, and this graph is shifted to the left.

I don't get the difference between these two problems, when they both have a negative x, and a positive integer. Why does one shift to the left, and one shifts to the right?

Linda
  • 11
  • What was the question? – Sassatelli Giulio Aug 21 '22 at 18:41
  • In both the cases, the graph indeed shifts right. (Not left in the latter case). – VoidGawd Aug 21 '22 at 18:48
  • InanimateBeing, I now see that you are correct, and I'm not sure why I thought the second one was shifted left. I think I just needed a break from this topic, and perhaps more practice and thought about the order of operations. – Linda Aug 21 '22 at 19:02
  • In your second example $y=-2(3)^{5-x}$ think of it as replacing $y=2(3)^{5-x}$ with $-y=2(3)^{5-x}$. When $y$ is replaced with $-y$ the graph is reflected about the $x$-axis. All examples of graphing $y=-f(x)$ should be conceptualized as replacing $y$ with $-y$. Then it is clear that the logic is the same as when replacing $x$ with $-x$. Otherwise one is left with a semblance of inconsistency in the operations. – John Wayland Bales Aug 22 '22 at 00:09
  • Welcome to this site! If the issue has been resolved, do consider accepting ✔ and upvoting ▲ answers: this signals resolution, prevents the page from being bumped, scores points, and influences the site's search results, cleanup activities, and other behind-the-scenes processes. – VoidGawd Aug 24 '22 at 20:03

1 Answers1

1

Let's do the graph transformation for both (starting from step $0$): $$y=\sqrt x$$
1

$$y=\sqrt {-x}$$
2

$$y=\sqrt {-(x-4)}$$
3

$$y=K^x$$
4

$$y=-K^x$$
5

$$y=-K^{-x}$$
6

$$y=-K^{-(x-5)}$$
7

In case you ever have confusion, you may refer this link on Graph Transformation.

VoidGawd
  • 3,110