it's binary quadratic forms, indefinite. Say $\frac{x}{1-x-x^2} = k$ is a positive integer. We have $x = k - kx - k x^2$ and $k-(k+1)x - k x^2 =0,$ and we demand $x$ rational.
So far, $ k x^2 +(k+1)x - k=0.$ The Quadratic Formula says
$$ x = \frac{-1-k \pm \sqrt{(k+1)^2 +(2k)^2}}{2k} $$ so
in order to have $x$ rational, we demand
$$ (k+1)^2 + (2 k)^2 = w^2 $$
There are two cases, both need a diagram. WHEN $k$ is even, $\gcd( k+1, 2k) = 1.$ Thus we have a primitive Pythagorean triple. The requirement is that there be integers $m,n$ coprime and not both odd, with $2mn=2k, m^2 - n^2 = k+1. $ Thus $mn=k$ and
$$ m^2 - mn - n^2 = 1.$$
Negating both sides gives
$$ n^2 + nm - m^2 = -1$$
All solutions of this can be shown on Conway's topograph, I usually write the form as $x^2 + xy - y^2 $ because it is Gauss-Lagrange reduced...
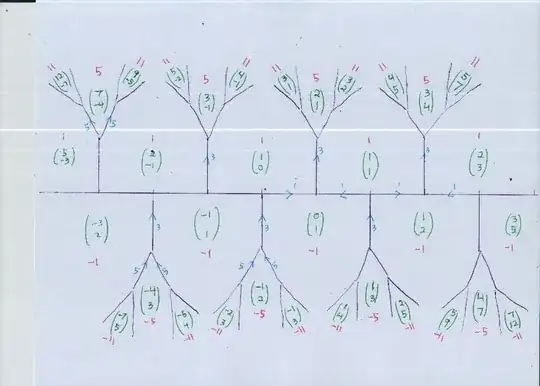The diagram shows that the value of $x^2 + xy - y^2$ is unchanged by the mapping (same idea as Vieta Jumping)
$$ (x,y) \mapsto (x+y, x+2y) $$
and a little fiddling shows that the $(x,y)$ pairs (with $x,y \geq 0$) and $x^2 + xy - y^2 = -1$ are
$$ (0,1), (1,2), (3,5), (8,13), (21,34), (55, 89) $$ and so on. Indeed, inverting the mapping to $ (x,y) \mapsto (2x-y, -x+y) $ takes any pair back to $(0,1),$ this giving the proof of Fibonacci-ness
Then we go back to $k=mn$ which is, in the diagram, $k=xy,$ after which the desired rational number (originally called $x$ ) is
$$ x = \frac{-1-k \pm \sqrt{(k+1)^2 +(2k)^2}}{2k} $$
The values of $k$ are
$$ 0, 2, 15, 104, 714, 4895, $$
with $ k_{n+2} = 7 k_{n+1} - k_n + 1$
SECOND CASE: when $k$ is odd, we may write $k = 2j+1$ and reach $(j+1)^2 +( 2j+1)^2 = w^2.$ The two numbers $j+1, 2j+1$ are coprime, the latter odd, thus $j+1$ is even and $j$ odd. Once again, $j+1 = 2mn$ so that $2j+2 = 4mn, $ while
$2j+1 = m^2 - n^2 $ As $2j+1 - (2j+2) = -1,$ we find
$$m^2 - 4mn - n^2 = -1$$ I would usually switch to
$$ n^2 + 4nm - m^2 = 1. $$ I don't expect I have a diagram ready for this exact form.
As is a requirement for representing $1,$ all $(n,m)$ pairs arise by beginning with $(1,0) $ and applying the automorphism matrix generator to reach mapping
$$ (n,m) \mapsto (n+4m, 4n+17m)$$
The first few pairs with both nonnegative are
$$ (1,0), (1,4), ( 17, 72), (305, 1292), (5473, 23184), ...$$
Both sequences, $1,1, 17, 305, 5473, ... $ and
$0, 4, 72, 1292, 23184$ obey the recurrence
$n_{j+2} = 18 n_{j+1} - n_j$ and $m_{j+2} = 18 m_{j+1} - m_j.$ For this one,
$k = m^2 - n^2 $ and begins
$$ -1, 15, 4895, 1576239, 507544127, 163427632719, 52623190191455, 16944503814015855, ...$$
Here we have recurrence
$$ k_{i+2}= 322 k_{i+1} - k_i + 64 $$
If we name $w_i = \sqrt{5k_i^2 + 2 k_i + 1},$ beginning with $k=-1$ we get sequence
$$ 2, 34, 10946, 3524578, 1134903170, 365435296162, 117669030460994, $$
$$ w_{i+2}= 322 w_{i+1} - w_i $$
