Short version: in $w^2 - 5 v^2 = 4,$ the numbers $v$ are Fibonacci numbers, of which the largest perfect square is $144$
As you can see, my "v" numbers are alternate Fibonacci numbers, while "w" are Lucas. I will try to find a reference, it is known that the largest square Fibonacci number is 144. Your largest $n$ is therefore $12,$ where your $m=322$
COHN 1963
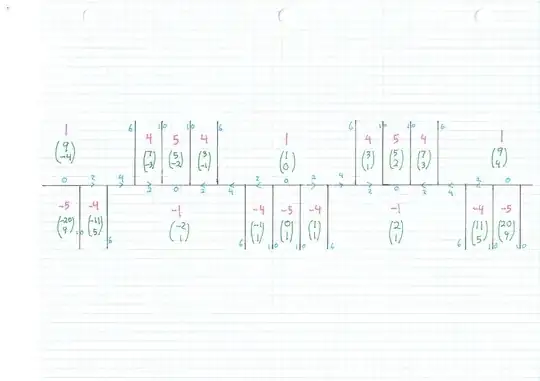
Umm. Here is a Conway topograph for the quadratic form $x^2 - 5 y^2.$ This constitutes a proof that all solutions of $x^2 - 5 y^2 = 4$ are generated by initial pairs
$$ (2,0) , (3,1) , ( 7,3), (18,8), (47,21), 123,55), (322,144), (843, 377) $$
with recursions
$$ x_{n+6} = 18 x_{n+3} - x_n $$
$$ y_{n+6} = 18 y_{n+3} - y_n $$
These are from Cayley-Hamilton for
$$
\left(
\begin{array}{cc}
9&20 \\
4&9
\end{array}
\right)
$$
A little more work shows that we may interpolate, meaning
$$ x_{n+2} = 3 x_{n+1} - x_n $$
$$ y_{n+2} = 3 y_{n+1} - y_n $$
Let's see, the irrationals in the Binet description of alternate Fibonacci numbers are
$$ \frac{3 \pm \sqrt 5}{2}, $$
while
$$ \left(\frac{3 \pm \sqrt 5}{2} \right)^3 = 9 \pm 4 \sqrt 5 $$
where $9 \pm 4 \sqrt 5$ are the Binet numbers from $\lambda^2 - 18 \lambda + 1 =0$
REsources on Conway's Topograph
http://www.maths.ed.ac.uk/~aar/papers/conwaysens.pdf (Conway)
https://www.math.cornell.edu/~hatcher/TN/TNbook.pdf (Hatcher)
http://bookstore.ams.org/mbk-105/ (Weissman)
http://www.springer.com/us/book/9780387955872 (Stillwell)
Generate solutions of Quadratic Diophantine Equation
diagrams
Another quadratic Diophantine equation: How do I proceed?
How to find solutions of $x^2-3y^2=-2$?
Generate solutions of Quadratic Diophantine Equation
Why can't the Alpertron solve this Pell-like equation?
Finding all solutions of the Pell-type equation $x^2-5y^2 = -4$
If $(m,n)\in\mathbb Z_+^2$ satisfies $3m^2+m = 4n^2+n$ then $(m-n)$ is a perfect square.
how to solve binary form $ax^2+bxy+cy^2=m$, for integer and rational $ (x,y)$ :::: 69 55
Find all integer solutions for the equation $|5x^2 - y^2| = 4$
Positive integer $n$ such that $2n+1$ , $3n+1$ are both perfect squares
Maps of primitive vectors and Conway's river, has anyone built this in SAGE?
Infinitely many systems of $23$ consecutive integers
Solve the following equation for x and y: <1,-1,-1>
Finding integers of the form $3x^2 + xy - 5y^2$ where $x$ and $y$ are integers, using diagram via arithmetic progression
Small integral representation as $x^2-2y^2$ in Pell's equation
Solving the equation $ x^2-7y^2=-3 $ over integers
Solutions to Diophantine Equations
How to prove that the roots of this equation are integers?
Does the Pell-like equation $X^2-dY^2=k$ have a simple recursion like $X^2-dY^2=1$?
http://math.stackexchange.com/questions/1737385/if-d1-is-a-squarefree-integer-show-that-x2-dy2-c-gives-some-bounds-i/1737824#1737824 "seeds"
Find all natural numbers $n$ such that $21n^2-20$ is a perfect square.
Is there a simple proof that if $(b-a)(b+a) = ab - 1$, then $a, b$ must be Fibonacci numbers? 1,1,-1; 1,11
To find all integral solutions of $3x^2 - 4y^2 = 11$
How do we solve pell-like equations?
Diophantine equation $x^2 + xy − 3y^2 = 17$ <1,1,-3>
jagy@phobeusjunior:~$ ./Pell_Target_Fundamental
Automorphism matrix:
9 20
4 9
Automorphism backwards:
9 -20
-4 9
9^2 - 5 4^2 = 1
w^2 - 5 v^2 = 4 = 2^2
Thu Nov 19 10:06:08 PST 2020
w: 2 v: 0 SEED KEEP +-
w: 3 v: 1 SEED KEEP +-
w: 7 v: 3 SEED BACK ONE STEP 3 , -1
w: 18 v: 8 SEED BACK ONE STEP 2 , 0
w: 47 v: 21
w: 123 v: 55
w: 322 v: 144
w: 843 v: 377
w: 2207 v: 987
w: 5778 v: 2584
w: 15127 v: 6765
w: 39603 v: 17711
w: 103682 v: 46368
w: 271443 v: 121393
w: 710647 v: 317811
w: 1860498 v: 832040
w: 4870847 v: 2178309
w: 12752043 v: 5702887
Thu Nov 19 10:06:37 PST 2020
w^2 - 5 v^2 = 4 = 2^2
