If $a+b=1$ then $a^{4b^2}+b^{4a^2}\leq1$

Question

Let $a$ and $b$ be positive numbers such that $a+b=1$. Prove that: $$a^{4b^2}+b^{4a^2}\leq1$$

I think this inequality is very interesting because the equality "occurs" for $a=b=\frac{1}{2}$ and also for $a\rightarrow0$ and $b\rightarrow1$.

I tried to work with a function of one variable, but the derivative is not easy.

I also don't get something solvable by Taylor series.

Answer 1

We define $f(x,y)=x^{4y^2}+y^{4x^2}$.

This is my plan to solve the problem:

• Since $x+y=1$, we replace $y$ by $1-x$.
• We make a new function: $g(x)=x^{4(1-x)^2}+(1-x)^{4x^2}$
• Therefore, we must find the maximum on the range $x \in [0,1]$ of $g$ so that we can see the maximum is less than or equal to $1$.

This will be troublesome:

$$g(x)=x^{4(1-x)^2}+(1-x)^{4x^2}$$

Set $g_{1}(x) = x^{4(1-x)^2}$ and $g_{2}(x) = (1-x)^{4x^2}$. Therefore, we can break it up like so:

$$g'(x) = g_{1}'(x)+g_{2}'(x)$$ $$g_{1}'(x)=g_{1}', g_{2}'(x)=g_{2}'$$ $$\ln(g_{1})=\ln \left(x^{4(1-x)^2}\right)$$ $$\ln(g_{1})={4(1-x)^2} \cdot \ln \left(x\right)$$ $$\frac{g_{1}'}{g_{1}}= 4 \cdot \left((1-x)^2 \right)' \cdot \ln(x)+\frac{4(1-x)^2}{x}$$ $$\frac{g_{1}'}{g_{1}}= 4 \cdot -2 \cdot (1-x) \cdot \ln(x)+\frac{4(1-x)^2}{x}$$ $$\frac{g_{1}'}{g_{1}}= 8(x-1)\ln(x)+\frac{4x^2-8x+4}{x}$$ $$\frac{g_{1}'}{g_{1}}= 8(x-1)\ln(x)+4x-8+\frac{4}{x}$$ $$g_{1}'= x^{4(1-x)^2} \cdot \left(8(x-1)\ln(x)+4x-8+\frac{4}{x}\right)$$

Alright. Deep breath. Let's keep going.

$$\ln(g_{2})=4x^2\ln(1-x)$$ $$\frac{g_{2}'}{g_{2}}=8x\ln(x-1)+\frac{4x^2}{x-1}$$

$$g_{2}'= (1-x)^{4x^2}\left(8x\ln(x-1)+\frac{4x^2}{x-1}\right)$$

$$g_{1}'= x^{4(1-x)^2} \cdot \left(8(x-1)\ln(x)+4x-8+\frac{4}{x}\right)$$

$$g'(x)=x^{4(1-x)^2} \cdot \left(8(x-1)\ln(x)+4x-8+\frac{4}{x}\right) + (1-x)^{4x^2}\left(8x\ln(1-x)+\frac{4x^2}{x-1}\right)$$

The maximum appears (according to the closed interval method), either at:

$$g(0)=1$$ $$g(1)=1$$

Or at the $x$-value(s) of the solution of:

$$0=x^{4(1-x)^2} \cdot \left(8(x-1)\ln(x)+4x-8+\frac{4}{x}\right) + (1-x)^{4x^2}\left(8x\ln(1-x)+\frac{4x^2}{x-1}\right)$$

Therefore, if we set $x_{1}$, $x_{2}$, $x_{3}$ ... to be the solutions to the equation above in the interval $x_{n} \in [0,1]$, we have reduced the problem to proving that:

$$g(x_{1}),g(x_{2}), g(x_{3})... \leq 1$$

Through some graphing of $g(x)$, we see that there exists $x_{1}$, $x_{2}$, and $x_{3}$, where $x_{2}$ is $0.5$ and the others are not easily calculatable or are irrational.

It can easily be seen that $g'(0.5) = 0$ and that $g(0.5)=1$ (a maximum of the function). Since we now have proof that $g(x_{2}) \leq 1$ and we see that there does not exist an $x_{n}$ s.t. $n>3$ and $g'(x_{n})=0$, we can reduce our previous problem to:

Prove that:

$$g(x_{1}), g(x_{3}) \leq 1$$

Through Newton's Method, we obtain approximations of $x_{1}$ and $x_{3}$ accurate to 10 decimal places. We state them below:

$$x_{1} \approx 0.281731964017$$ $$x_{3} \approx 0.718268035983$$

Note that:

$$g'(x_{1}) \approx g'(0.281731964017)=7.349676423 \cdot 10^{-14}$$ $$g(x_{1}) \approx g(0.281731964017)=0.973494223187$$

We now have that $g(x_{1})$ is a minimum of the function and that $g(x_{1}) \leq 1$

Finally:

$$g'(x_{3}) \approx g'(0.718268035983)=-7.349676423 \cdot 10^{-14}$$ $$g(x_{3}) \approx g(0.718268035983)=0.973494223187$$

We now have that $g(x_{1})$ is also a minimum of the function and that $g(x_{1}) \leq 1$

We now have that:

$$g(x_{1}), g(x_{2}), g(x_{3}) \leq 1$$

Q.E.D

I took a very head-on brute-force approach to the problem, but I am happy with the rigorousness of the result and the final proof. We also now have the minimums of the function, which if anyone is curious, is $\approx 0.973494223187$

Answer 2

Let $f \colon [0,1] \rightarrow \mathbb{R}$ be the function given by $$f(x) = x^{4 (1-x)^2}.$$ We will show that if $x \in [0,\frac{1}{2}]$ then $f(x) + f(1-x) \leq 1$.

If $x=0$ then it is clear that $f(0)+f(1)=1$.

Claim 1. If $x \in (0, \frac{71}{200}]$ then $f(x) + f(1-x) \leq 1$.

Proof. Let $x \in (0, \frac{71}{200}]$. By Bernoulli's inequality we have $$f(1-x) = (1-x)^{4x^2} \leq 1-4x^3.$$ Therefore \begin{align} &f(x) + f(1-x) \leq 1 \\ &\impliedby f(x) \leq 4x^3 \\ &\iff \log x^{4 (1-x)^2} \leq \log4x^3 \\ &\iff (3-4 (1-x)^2) \log x\ + \log 4 \geq 0. \end{align} The $\log x$ is a problem here. We use the following trick to factor our expression.

Since the global maximum of $z \mapsto - z \log z$ is $\mathrm{e}^{-1}$, we have $(-\mathrm{e}\, x \log x) \log 4 \leq \log 4.$ It follows that \begin{align} &(3-4 (1-x)^2) \log x\ + \log 4 \geq 0 \\ &\impliedby (3-4 (1-x)^2 -(\mathrm{e}\ \log 4)\, x) \log x\ \geq 0 \\ &\iff 3-4 (1-x)^2 -(\mathrm{e}\ \log 4)\, x \leq 0 \\ &\impliedby x \leq \frac{71}{200} < \frac{1}{4} \left(4-\mathrm{e} \log 2-\sqrt{12+\mathrm{e}^2 \log ^2 2-8 \mathrm{e} \log 2}\right). \end{align} We used the quadratic formula in the last step. $$\tag*{$\Box$}$$

Claim 2. If $x \in (\frac{71}{200}, \frac{73}{200}]$ then $f(x) + f(1-x) < 1$.

Proof. Let $z \in (0,1)$. Since $\log(z) \leq z-1$, we have

\begin{align} f'(z) &= x^{4 (1-z)^2} \left(\frac{4 (1-z)^2}{z}-8 (1-z) \log z\right) \\ &\geq x^{4 (1-z)^2} \left(\frac{4 (1-z)^2}{z}+8 (1-z)^2\right) \geq 0. \end{align}

Thus $f$ is monotonically increasing on $(0,1)$. We have $$f(x) + f(1-x) \leq f\left(\frac{73}{200}\right) + f\left(1-\frac{71}{200}\right) \approx 0.9985 < 1$$ for all $x \in (\frac{71}{200}, \frac{73}{200}]$. $$\tag*{$\Box$}$$

We need some lemmata for $(\frac{73}{200}, \frac{1}{2}]$.

Let $\varphi \colon (-\frac{1}{2},\frac{1}{2}) \rightarrow \mathbb{R}$ be the function given by $\varphi(z) = \log \left(\frac{1}{2}-z\right).$

Lemma 3.1. If $z \in (-\frac{1}{2},\frac{1}{2})$ then $\varphi(z) \leq -\log 2 -2 z-2 z^2-\frac{8}{3}z^3$.

Proof. Let $z \in (-\frac{1}{2},\frac{1}{2})$. Since $\log$ is real analytic, we have \begin{align} \varphi(z) &= \sum_{k=0}^{\infty} \frac{\varphi^{(k)}(0)}{k!}z^k \\&=-\log 2 -2 z-2 z^2-\frac{8}{3}z^3 + \sum_{k=4}^{\infty} \frac{\varphi^{(k)}(0)}{k!}z^k. \end{align} By the Lagrange form of the remainder there is a $\zeta \in (-\frac{1}{2},\frac{1}{2})$ such that $$\frac{\varphi^{(4)}(\zeta)}{4!}z^4 = \sum_{k=4}^{\infty} \frac{\varphi^{(k)}(0)}{k!}z^k.$$ We have \begin{align} \varphi(z) &= -\log 2 -2 z-2 z^2-\frac{8}{3}z^3 + \frac{\varphi^{(4)}(\zeta)}{4!}z^4 \\ &= -\log 2 -2 z-2 z^2-\frac{8}{3}z^3 -\frac{1}{4\left(\frac{1}{2}-\zeta\right)^4} z^4 \\ &\leq -\log 2 -2 z-2 z^2-\frac{8}{3}z^3. \end{align} $$\tag*{$\Box$}$$

Let $\gamma \colon (-\frac{1}{2},\frac{1}{2}) \rightarrow \mathbb{R}$ be the function given by $$\gamma(z) = 4 \left(z+\frac{1}{2}\right)^2 \left(-\log 2 -2 z-2 z^2-\frac{8}{3}z^3\right).$$

Lemma 3.2. If $z \in [-\frac{27}{200},\frac{27}{200}]$ then $$-\frac{1}{2}\left(\frac{\gamma(z)-\gamma(-z)}{2}\right)^2-\log 2\geq \frac{\gamma(z)+\gamma(-z)}{2}.$$ Proof. The inequality is equivalent to $$-128 z^8-448 z^6+z^4 (-440-96 \log 2)+z^2 (-42-168 \log2)+18-18 \log ^2 2 -9 \log 2 \geq 0.$$

We substitute $u = z^2$ and use the quartic formula to calculate the roots of the polynomial. The real roots are near $-0.136139$ and $0.136139$. We have $$-0.136 < -\frac{27}{200} < \frac{27}{200} < 0.136.$$ We calculate that the inequality holds at $z=0$, thus it must hold for all $z \in [-\frac{27}{200},\frac{27}{200}]$. $$\tag*{$\Box$}$$

Let $\psi \colon \mathbb{R} \rightarrow \mathbb{R}$ be the function given by $$\psi(z) = \exp\left(-\frac{z^2}{2}\right)(\exp(z) + \exp(-z)).$$

Lemma 3.3. If $z \in \mathbb{R}$ then $\psi(z) \leq 2$.

Proof. For all $z \in [0, \infty)$ we have \begin{align} \exp\left(\frac{z^2}{2}+z\right)\psi'(z) &= -1 -z -(z-1)\exp(2 z) \\ &= -1 -z -(z-1) \sum_{k=0}^{\infty}\frac{2^k z^k}{k!} \\ &= -1 -z - (z-1) \sum_{k=0}^{\infty}\frac{2^k z^k}{k!} \\ &= -1 -z + \sum_{k=0}^{\infty}\frac{2^k z^k}{k!} - \sum_{k=1}^{\infty}\frac{2^{k-1} z^{k}}{(k-1)!} \\ &= -z + \sum_{k=1}^{\infty}2^{k-1}\left(\frac{2}{k!} - \frac{1}{(k-1)!}\right) z^k \\ &= -z + \sum_{k=1}^{\infty}2^{k-1}\left(\frac{2 (k-1)!-k!}{(k-1)! k!}\right) z^k \\ &= \sum_{k=3}^{\infty}2^{k-1}\left(\frac{2 (k-1)!-k!}{(k-1)! k!}\right) z^k. \end{align} Since $2 (k-1)! < k!$ for all $k > 2$, we have $\psi'(z) \leq 0$. Thus $\psi$ is monotonically decreasing on $[0,\infty)$. We have $\psi(0) = 2$, thus $\psi(z) \leq 2$ for all $z \in [0,\infty)$. Since $\psi(z) = \psi(-z)$ for all $z \in \mathbb{R}$, we have $\psi(z) \leq 2$. $$\tag*{$\Box$}$$

Claim 3.4. If $x \in (\frac{73}{200}, \frac{1}{2}]$ then $f(x) + f(1-x) \leq 1$.

Proof. Let $x \in (\frac{73}{200}, \frac{1}{2}]$ and $z = \frac{1}{2} - x \in [0, \frac{27}{200})$. We have

\begin{align} f(x) + f(1-x) &= f\left(\frac{1}{2}-z\right) +f\left(\frac{1}{2}+z\right) \\[10pt] &= \exp \left(4 \left(\frac{1}{2}+z\right)^2 \varphi(z)\right) + \exp \left(4 \left(\frac{1}{2}-z\right)^2 \varphi(-z)\right) \\ \text{By Lemma 3.1:} \\[7pt] &\leq \exp \left(\gamma(z)\right) + \exp \left(\gamma(-z)\right) \\[10pt] &= \exp \frac{\gamma(z)+\gamma(-z)}{2} \left(\exp \frac{\gamma(z)-\gamma(-z)}{2} + \exp \frac{\gamma(-z)-\gamma(z)}{2}\right) \\ \text{By Lemma 3.2:} \\[7pt] &\leq \exp \left(-\frac{1}{2}\left(\frac{\gamma(z)-\gamma(-z)}{2}\right)^2-\log 2\right) \left(\exp \frac{\gamma(z)-\gamma(-z)}{2} + \exp \frac{\gamma(-z)-\gamma(z)}{2}\right) \\[10pt] &= \frac{1}{2}\, \exp \left(-\frac{1}{2}\left(\frac{\gamma(z)-\gamma(-z)}{2}\right)^2\right) \left(\exp \frac{\gamma(z)-\gamma(-z)}{2} + \exp \frac{\gamma(-z)-\gamma(z)}{2}\right) \\[10pt] &= \frac{1}{2}\, \psi\left(\frac{\gamma(z)+\gamma(-z)}{2}\right) \\ \text{By Lemma 3.3:} \\[7pt] &\leq 1. \end{align} $$\tag*{$\Box$}$$

Answer 3

I offer a complete, self-contained solution below that can be checked without computer/calculator assistance.

The main tools that we will use (abuse?) are logarithmic differentiation and symmetry, to greatly simplify the exponentials that we are dealing with.

We may assume that $0<a\leq\frac12\leq b<1$. We split into the following two cases.

Case 1: $a\leq\frac13$

By Bernoulli's inequality we have $b^{4a^2}=(1-a)^{4a^2}\leq1-4a^3$, so it suffices to show that $$a^{4(1-a)^2}\stackrel?<4a^3.$$ Let $h(a)=(4(1-a)^2-3)\ln(a)$; we want to show that $h(a)\stackrel?<\ln4$. Now $$h'(a)=\frac{4(1-a)^2-3}a-8(1-a)\ln(a)$$ can clearly be seen to be decreasing on $a\in[0,1]$ (edit: in fact this is false as stated, but writing $\frac{4(1-a)^2-3}a=\frac{(2a-1)^2}a-4$ we see that $h'(a)$ is decreasing for $a\in[0,\frac12]$). Hence $$h'(a)\geq h'(\frac13)=\frac{16\ln3-11}3>\frac{16-11}3>0,$$ so $h(a)$ is increasing on $a\in[0,\frac13]$. Thus $$h(a)\leq h(\frac13)=\frac{11}9\ln3<\ln4,$$ since $4^4=256>243=3^5$ implies $\frac{\ln4}{\ln3}>\frac54>\frac{11}9$, as desired.

Case 2: $\frac13\leq a\leq\frac12$

Substitute $a=\frac12-x$ and $b=\frac12+x$, so $x\in[0,\frac16]$ and $$b^{4a^2}+a^{4b^2}=\left(\frac12+x\right)^{(1-2x)^2}\!\!\!+\left(\frac12-x\right)^{(1+2x)^2}\!\!\!=F(x)+F(-x),$$ where $$F(x)=\left(\frac12+x\right)^{(1-2x)^2}\!\!\!.$$

Write $F'(x)=F(x)G(x)$ (so $G$ is the logarithmic derivative of $F$). It is clear that $F(x)$ is increasing on $x\in[-\frac16,\frac16]$, so $F(x),F'(x)>0$ implies $G(x)>0$ on $x\in[-\frac16,\frac16]$.

Now $F(0)+F(-0)=1$, so \begin{align*} F(x)+F(-x)\stackrel?\leq1 &\:\Longleftarrow\:\frac d{dx}(F(x)+F(-x))\stackrel?\leq0\\ &\iff F'(x)\stackrel?\leq F'(-x)\\ &\iff\frac{F(x)}{F(-x)}\stackrel?\leq\frac{G(-x)}{G(x)}. \end{align*} We now prove this last inequality on $x\in[0,\frac16]$ in the following steps.

Step 1

We will show that $\ln\left(\dfrac{F(x)}{F(-x)}\right)$ is concave up on $x\in[0,\frac16]$, ie. \begin{align*} \frac{d^2}{dx^2}\ln\left(\dfrac{F(x)}{F(-x)}\right)&=\frac d{dx}(G(x)+G(-x))\\ &=G'(x)-G'(-x)\stackrel?\geq0. \end{align*} It suffices to show that $G'(x)$ is increasing on $x\in[-\frac16,\frac16]$. Now \begin{align*} G(x)&=\frac d{dx}\ln(F(x))\\ &=(1-2x)\left(\frac{1-2x}{\frac12+x}-4\ln\left(\frac12+x\right)\right),\\ G'(x)=\cdots&=\frac43\cdot\frac{-4+9(x+\frac16)^2}{(\frac12+x)^2}+8\ln\left(\frac12+x\right),\tag{*} \end{align*} so (by some miracle!) $G'(x)$ can be clearly seen to be increasing on $x\in[-\frac16,\frac16]$.

Hence the graph of $\ln\left(\dfrac{F(x)}{F(-x)}\right)$ lies below the line joining $(0,0)$ and $\left(\dfrac16,\ln\left(\dfrac{F(\frac16)}{F(-\frac16)}\right)\right)$, ie. $$\ln\left(\dfrac{F(x)}{F(-x)}\right)\leq6\ln\left(\dfrac{F(\frac16)}{F(-\frac16)}\right)x=2Cx,\quad C:=\frac{4\ln54}3.$$

Step 2

We are left to show that $\dfrac{G(-x)}{G(x)}\stackrel?\geq e^{2Cx}$ on $x\in[0,\frac16]$.

A little manipulation gives \begin{align*} \frac{G(x)}{\sqrt{1-4x^2}}&=\sqrt{\frac{1-2x}{1+2x}}\left(2\,\frac{1-2x}{1+2x}-4\ln\left(\frac12+x\right)\right)\\ &=u(2u^2+4\ln(1+u^2)):=H(u), \end{align*} under the substitution $u=\sqrt{\dfrac{1-2x}{1+2x}}$, $x=\dfrac12\,\dfrac{1-u^2}{1+u^2}$.

Now the desired inequality is equivalent to $$\frac{H(\frac1u)e^{-Cx}}{H(u)e^{Cx}}=\frac{G(-x)e^{-Cx}}{G(x)e^{Cx}}\stackrel?\geq1\quad\text{for }x\in[0,\tfrac16]\iff u\in[\tfrac1{\sqrt2},1].$$ Note that $u$ is decreasing in $x$, and the transformation $x\to-x$ is equivalent to $u\to\frac1u$. Thus it is sufficient to show that $H(u)e^{Cx}$ is increasing on $u\in[\frac1{\sqrt2},\sqrt2]$ (this is less than clear; I have gotten the sign wrong several times myself), ie. \begin{align*} \frac d{du}\ln(H(u)e^{Cx})&=\frac d{du}(Cx+\ln H(u))\\ &=C\frac{dx}{du}+\frac{H'(u)}{H(u)}\\ &=-2C\frac u{(1+u^2)^2}+\frac1u+\frac{2u+\frac{4u}{1+u^2}}{u^2+2\ln(1+u^2)}\stackrel?\geq0\\ \iff\frac{2C}{1+u^2}&\stackrel?\leq\frac{1+u^2}{u^2}+\frac{2(3+u^2)}{u^2+2\ln(1+u^2)}. \end{align*} We substitute $t=u^2$ and use the inequality $\ln(1+t)\leq\ln2+\frac{t-1}2$ (by convexity of $\ln(t+1)$; RHS is tangent line at $t=1$) to reduce the above to $$2+\frac1t+\frac{7-2\ln2}{2t+2\ln2-1}\stackrel?\geq\frac{2C}{1+t}.\tag{**}$$ This will fall to Cauchy-Schwarz (in the Engel form $\sum\dfrac{a_i^2}{b_i}\geq\dfrac{(\sum a_i)^2}{\sum b_i}$), if we can find the correct weights. With some (okay, a lot) of inspiration, we obtain the following: \begin{align*} &\phantom{{}={}}2+\frac1t+\frac{7-2\ln2}{2t+2\ln2-1}\\ &\geq\frac{94}{47}+\frac{18}{18t}+\frac{101}{36+7t}\\ &\geq\frac{(\sqrt{94}+\sqrt{18}+\sqrt{101})^2}{54(1+t)}\geq\frac{2C}{1+t}, \end{align*} which is what we wanted.

Hence we are left with the following (zero-variable!) inequalities that we used above: $$\ln2\stackrel?\leq\frac{25}{36},\qquad\frac{(\sqrt{94}+\sqrt{18}+\sqrt{101})^2}{54}\stackrel?\geq2C.$$ Most people should be content with checking these by calculator. For the purists, here is a sketch of how to get these by hand.

Step 3 (Optional?)

Firstly, note that for $x>0$, we have \begin{align*} \ln\left(\frac{1+x}{1-x}\right)&=2\left(x+\frac{x^3}3+\frac{x^5}5+\frac{x^7}7+\cdots\right)\\ &\leq2\left(x+\frac{x^3}3+\frac{x^5}3+\frac{x^7}3+\cdots\right)\\ &=2\left(x+\frac{x^3}{3(1-x^2)}\right). \end{align*} Taking $x=\frac13$ gives the first inequality. In addition, taking $x=\frac15$ gives $$54(2C)=54\times\frac83\left(3\ln\frac32+\ln2\right)\leq72\left(3\times\frac{73}{180}+\frac{25}{36}\right)=\frac{2876}5.$$ Let $(a,b,c,d)=(101,94,18,\frac{2876}5)$, and $n=\frac12(c+d-a-b)$. We are left to check that \begin{align*} \sqrt a+\sqrt b+\sqrt c&\geq\sqrt d\\ \iff a+b+2\sqrt{ab}&\geq c+d-2\sqrt{cd}\qquad(\because\sqrt a+\sqrt b>0)\\ \iff\sqrt{ab}&\geq n-\sqrt{cd}\\ \iff ab&\geq n^2+cd-2n\sqrt{cd}\qquad(\because\sqrt{ab}>0)\\ \iff2n\sqrt{cd}&\geq n^2+cd-ab\\ \iff4n^2cd&\geq(n^2+cd-ab)^2,\qquad(\because2n\sqrt{cd}>0) \end{align*} which after substitution becomes $\dfrac{205212545208}{125}\geq\dfrac{16402832101681}{10000}$, something that I consider to be close to the limits of what I can do by hand.

QED. Phew!

Remarks

1. Yes, this might be a long proof, and perhaps it doesn't give much insight as to why the original inequality holds. However, I hope that the tricks used in the solution (and there are many!) are of independent interest.

2. I have optimised the solution as presented above to minimise the effort of hand calculations. Some parts of the solution have feasible alternatives, eg. at $(*)$ we can compute $G''(x)=\dfrac{16(7+8x+4x^2)}{(1+2x)^3}$, and check that the numerator is positive on $x\in[-\frac16,\frac16]$; at $(**)$ we essentially need $P(t)\geq0$ for some cubic $P$, and we can proceed by showing $$P(t)\geq k(t-\lambda)(t-\mu)^2+Q(t)$$ for good choices of $k,\lambda,\mu\in\mathbb R$ and $Q$ a quadratic in $t$.

3. How human is this solution? It is certainly human-checkable, but I have serious doubts as to whether a human can come up with a proof along these lines without computer assistance. As many previous answers have noted, the original inequality is very tight, and we cannot afford to lose more than $0.03$ in total throughout our proof.

   In addition, I can count about 8 places in Step 2 alone where I used the irreversible $\Leftarrow$ implication, ie. "to prove A it is sufficient to prove B." This is disastrous if B turns out to be false! I personally needed extensive computer aid to explore the problem space and avoid dead ends of this type --- this proof was made possible by around 2000--3000 Mathematica commands.

   For these two reasons, I doubt that there can be an unassisted proof using the normal tools of calculus (such as those in the above solution), let alone in a competition setting. Of course, maybe we just need some radical new insight or perspective. (I have not looked at the $W$ function closely, so maybe...?)

Cheers.

Answer 4

Update

I want to share some thought. Consider the more general problem $$ a^{n b^2} + b^{n a^2} \leq 1 $$ A key observation is the symmetry of the two terms $a^{n b^2} $ and $b^{n \ a^2} $. Due to the constraint $a + b = 1 $, the two terms are just $a^{n (1 - a)^2} $ and $ (1 - a)^{n a^2} $. So a substitution of $a \rightarrow 1 - a$ changes one term to the other. Conclusion : The LHS is a sum of two terms symmetric around the $a = 1/2 $.

Lemma W.l.o.g, suppose a function $f (x) $ in interval $[0, 1] $.If the function is monotonic and convex around $x=1/2$, then the "mirror average function" $g (x) = (f (x) + f (1 - x))/2 $ has a maximum at $x = 1/2 $.

Proof Just calculate to show $g' (1/2) = 0 $ and $g'' (x) = f'' (x)$

Corollary for concave $f(x)$ follows directly. This analysis does not answer the question, but hopefully will introduce some abstractness and shed more light on it.

Old Post

This should be a comment, but then I won't be able to post pictures. For the more general inequality:

$$ a^{n b^2}+b^{n a^2}\leq1 $$

I draw pictures for n = 0, 1, ..., 7. Each one has green dashed contour highlighting where the equality is satisfied. And of course, each one is overlaid with $a+b=1$. It's interesting to note only $n = 4$ is tightly bounded by the green contour, so it is a really special $n$ value.

Answer 5

This is indeed a hard nut, since convexity cannot be invoked to close the case. The following plot shows that the function $$f(x):=(1-x)^{4x^2}+x^{4(1-x)^2}\qquad(0\leq x\leq 1)$$ in fact never drops below $0.97\>$! (Compare Robin Aldabanx' answer)

At the moment I'm just able to show that $f(x)$ behaves as claimed near $x=0$ (and, by symmetry, near $x=1$) and near $x={1\over2}$.

If $0\leq x\leq{1\over2}$ then $0\leq4x^2\leq1$, and Bernoulli's inequality gives $$(1-x)^{4x^2}\leq1-4x^3\ .$$ On the other hand $$x^{4(1-x)^2}=x^4\cdot x^{-8x+4x^2}=:x^4\> h(x)$$ with $\lim_{x\to0+}h(x)=1$. It follows that there is a $\delta>0$ with $$f(x)\leq 1-4x^3+2x^4=1-4x^3\>\left(1-{x\over2}\right)<1\qquad (0<x<\delta)\ .$$ For $x\doteq{1\over2}$ we consider the auxiliary function $$g(t):=f\left({1\over2}+t\right)\qquad\bigl(|t|\ll1\bigr)$$ which is analytic for small $|t|$. Mathematica computes its Taylor series as $$g(t)=1+\left(-8+4\log 2+8\log^2 2\right) t^2+\ ?\>t^3\ .$$ The numerical value of the relevant coefficient here is $\doteq-1.38379$, and this tells us that $f$ has a local maximum at $x={1\over2}$.

Answer 6

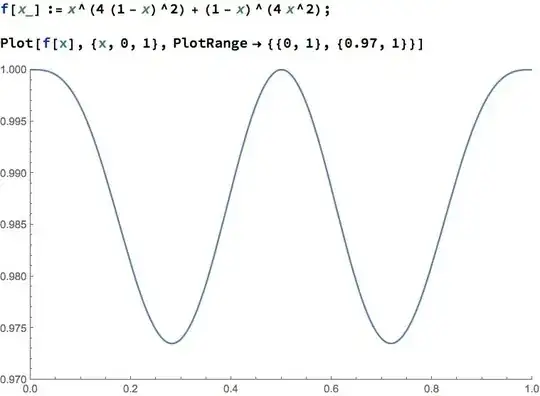
Too long for a comment .

It's just to propose one methods on power series .

Method (Power series)

First we have two inequalities ($\forall x\in[\frac{42}{100},\frac{1}{2}]$)

$$(1-x)^{4x^2}\leq \frac{1}{2}+\frac{2}{5} (\frac{1}{2}x-x^2)+ (\frac{-(2+4\ln(\frac{1}{2}))}{2}+\frac{18}{10}) (\frac{1}{2}-x)\quad(1)$$

And

$$x^{4(1-x)^2}\leq \frac{1}{2}+\frac{2}{5} (\frac{1}{2}x-\frac{1}{4})+ (\frac{-(2+4\ln(\frac{1}{2}))}{2}+\frac{18}{10}+\frac{2}{5}(x-\frac{1}{2}))(x-\frac{1}{2})$$

proof of $(1)$ :

Taking logartihm on both side then making the difference and differentiate and using :

$$8x\ln(1-x)\geq (0.5-\frac{2235}{1000}(0.5-x))\ln(0.5)$$

We get a fourth degree polynomial with a roots at $x=0.5$.Remains to study a third degree polynomial wich is not hard .

The proof of $(2)$ is similar .

For the case $\forall x\in[0,\frac{1}{3}]$ we can use the Bernoulli's inequality as in others answer . Remains just to prove the inequality on $[\frac{1}{3},\frac{45}{100}]$.I continue to explore this .

Another approach :

We use a form of the Young's inequality wich is a somewhere a generalization of the Bernoulli's inequality :

Let $a,b>0$ and $0<v<1$ then we have :

$$av+b(1-v)\geq a^vb^{1-v}$$

Taking account of this theorem and putting :

$a=x^{2(1-x)}$$\quad$$b=1$$\quad$$v=2(1-x)$ we get $0.5\leq x<1$:

$$x^{4(1-x)^2}\leq x^{2(1-x)}2(1-x)+1-2(1-x)$$

Now the idea is to show :

Let $$(1-x)^{4x^2}\leq 1-(x^{2(1-x)}2(1-x)+1-2(1-x))$$

Or :

$$(1-x)^{4x^2}\leq2(1-x)(1-x^{2(1-x)})$$

Or: $$(1-x)^{4x^2-1}+2x^{2(1-x)}\leq 2$$

Now by Bernoulli's inequality we have :

$$2x^{2(1-x)}\leq 2-4(1-x)^2$$

So :

$$(1-x)^{4x^2-1}+2-4(1-x)^2\leq 2$$

Or :

$$(1-x)^{4x^2-3}\leq 4$$

It's not hard to show it on $[0.65,1)$

As you can see here we can improve the reasoning above and get the inequality on $[0.61,1]$

Update 20/04/2021

We can improve the reasoning using the inequality :

$$(1-v)a+vb\geq a^{1-v}b^{v}+\min{(1-v,v)}(\sqrt{a}-\sqrt{b})^2$$

Found in this article (Proposition 1.1) https://arxiv.org/pdf/1001.0535.pdf

Edit :

We have the inequality for $0<x\leq 0.55$

$$\left(\frac{1}{1-\left(1-\frac{1}{1-\left(1-x\right)^{2\left(x\right)}}\right)\left(2^{-y}x^{-y}\right)}\right)\geq x^{4\left(1-x\right)^{2}}\quad (I)$$

Where $y=\frac{-(2+4\ln(\frac{1}{2}))}{2}+1$

We have also $0<x<1$:

$$r(x)=\left(\left(\frac{1}{1+\left(\frac{g\left(x\right)}{1-\left(1-x\right)^{2x}}-g\left(x\right)\right)2^{-f\left(x\right)}x^{-f\left(x\right)}}\right)^{-1}-1+g\left(x\right)\right)^{-1}\geq x^{4\left(1-x\right)^{2}}$$

Where :

$f(x)=-\frac{\left(2+4\ln\left(0.5\right)\right)}{2}+1$

And :

$g\left(x\right)=x^{2\left(1-x\right)}+\left(1-x\right)^{2x}$

To finish we have for $\frac{1}{4}\leq x\leq \frac{3}{4}$:

$$r(x)+r(1-x)\leq 1$$

A good start to show the inequality $(I)$ see WA.The same idea can be applied to the next inequality.

To simplify a little bit $(I)$ we have the inequality for $0.47\leq x\leq 0.53$ :

$$\left(1+\left(\frac{1}{1-\left(2^{\left(2\left(1-x\right)+1\right)}\cdot\left(1-x\right)^{2}\cdot x\right)}-1\right)\cdot2^{-\left(-\frac{\left(2+4\ln\left(0.5\right)\right)}{2}+1\right)}\cdot x^{-\left(-\frac{\left(2+4\ln\left(0.5\right)\right)}{2}+1\right)}\right)\cdot x^{4\left(1-x\right)^{2}}\leq 1$$

Last edit :

It seems we have on $x\in[0.45,0.55]$ :

$$\frac{\left(2^{-\left(2\left(1-x\right)\right)^{2}}\cdot x\right)}{1-2^{\ln\left(2\right)}\left(\left(1-x\right)\cdot2\cdot x\right)^{\left(\ln\left(2\right)+1\right)}}\geq x^{\left(2\left(1-x\right)\right)^{2}}$$

Edit 21/09/2022 :

We have the inequality for $x\in(0,0.75]$:

$$\left(\left(x\right)^{b}\cdot\frac{1}{1-\left(\left(1-x\right)^{b}-1\right)\left(x^{b}-1\right)}\right)^{a}\geq f(x)=1-\left(\left(1-x\right)^{b}\cdot\frac{1}{1-\left(\left(1-x\right)^{b}-1\right)\left(x^{b}-1\right)}\right)^{a}\geq x^{4\left(1-x\right)^{2}}$$

Where $$a,b=-\frac{\ln\left(2-2^{\frac{1}{a}}\right)}{\ln\left(2\right)}$$

And $a$ is choose as :

$$f'(1/2)=1+2\ln2$$

We can also improve it for $a,b$ as above and $x\in[1/3,1)$ :

Choosing :

$$f\left(x\right)=\left(\left(1-x\right)^{b}\cdot\frac{1+4\left(\left(x-0.5\right)\left(x-1\right)x\right)^{2}}{1-\left(\left(1-x\right)^{b}-1\right)\left(x^{b}-1\right)+4\left(\left(x-0.5\right)\left(x-1\right)x\right)^{2}}\right)^{a}$$

Answer 7

Again too long for comment

The inequality is equivalent to on $(0,0.5)$:

$$f(x)=\left(\left(x^{-\left(2\left(1-x\right)\right)^{2}}\right)-1\right)\left(\left(1-x\right)^{-\left(2x\right)^{2}}-1\right)\geq1$$

Now define :

$$u(x)=1+\frac{\left(\sqrt{1+0.0025\left(\frac{\left(\ln\left(m\left(x\right)\right)\right)}{\ln\left(2\right)}\right)^{\frac{\ln\left(64\right)}{3}}\cdot\left(\ln\left(\frac{m\left(x\right)}{2}\right)\right)^{2}}\right)-1}{0.00125\left(\ln\left(\frac{m\left(x\right)}{2}\right)\right)^{2}}$$

Where $m(x)=x^{-\left(2\left(1-x\right)\right)^{2}}$ and $g\left(x\right)=\left(\left(1-x\right)^{-\left(2x\right)^{2}}-1\right)$

We have the inequalities :

$$f(x)+(u(x)-1)g(x)\geq 2$$

$$f(x)\geq \frac{\left(\left(u\left(1-x\right)\right)\cdot\left(u\left(x\right)\right)\right)^{0.25}}{\sqrt{2}}\geq 1$$ This kind of method is valid for a generalisation when the higher exponent (here $2$ in $f(x)$) is greater or equal to $2$.