Improper Integral: $\int\limits_0^1\frac{\ln(x)}{x^2-1}\,dx$

Question

How can I prove that: $$\int\limits_0^1\frac{\ln(x)}{x^2-1}\,dx = \frac{\pi^2}{8}?$$

I know that:

$$\int\limits_0^1\frac{\ln(x)}{x^2-1}\, dx = \sum_{n=0}^{\infty}\int\limits_0^1-x^{2n}\ln(x)\,dx=\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}=\frac{\pi^2}{8},$$

but I want another method.

Answer 1

$$\begin{align}\int_0^1\frac{\ln(x)}{x^2-1}dx&=\frac{1}{2}\left(\int_0^1\frac{\ln(u)}{u^2-1}du+\int_0^1\frac{\ln(v)}{v^2-1}dv\right)\\ &=\frac{1}{2}\left(\int_0^1\frac{\ln(u)}{u^2-1}du+\int_1^{\infty}\frac{\ln(v)}{v^2-1}dv\right)\\ &=\frac{1}{2}\left(\int_0^1\frac{\ln(u)}{u^2-1}du+\int_0^{\infty}\frac{\ln(u)}{u^2-1}du-\int_0^{1}\frac{\ln(u)}{u^2-1}du\right)\\ &=\frac{1}{2}\int_0^{\infty}\frac{\ln(u)}{u^2-1}du=\frac{1}{2}\times\frac{1}{2}\int_0^{\infty}\frac{\ln(u^2)}{u^2-1}du =\frac{1}{4}\int_0^{\infty}\frac{1}{1-u^2}\ln\left(\frac{1}{u^2}\right)du\\ &=\frac{1}{4}\int_0^{\infty}\frac{1}{1-u^2}\left[\ln\left(\frac{1+v}{1+u^2v}\right)\right]_{v=0}^{v=\infty}du\\ &=\frac{1}{4}\int_0^{\infty}\frac{1}{1-u^2}\left(\int_0^{\infty}\left(\frac{1}{1+v}-\frac{u^2}{1+u^2v}\right)dv\right)du\\ &=\frac{1}{4}\int_0^{\infty}\int_0^{\infty}\frac{1}{(1+v)(1+u^2v)}dv\,du=\frac{1}{4}\int_0^{\infty}\left(\frac{1}{1+v}\int_0^{\infty}\frac{1}{1+u^2v}du\right)dv\\ &=\frac{1}{4}\int_0^{\infty}\left(\frac{1}{1+v}\left[\frac{\tan^{-1}(\sqrt{v}u)}{\sqrt{v}}\right]_{u=0}^{u=\infty}\right)dv=\frac{1}{4}\times\frac{\pi}{2}\int_0^{\infty}\frac{1}{\sqrt{v}(1+v)}dv\\ &=\frac{\pi}{8}\int_0^{\infty}\frac{2w}{w(1+w^2)}dw=\frac{\pi}{8}\times2\left[\tan^{-1}(w)\right]_0^{\infty}=\frac{\pi}{8}\times2\times\frac{\pi}{2}=\frac{\pi^2}{8}.\end{align}$$

Answer 2

Consider the integral: $$I(m)=\int _{0}^{1}\!{\frac { \ln\left( x \right) ^{m-1}}{ {x}^{2}-1}}{dx} \quad:\quad \mathfrak{R}(m)>1 $$ and the substitution $x=e^{-u}$: $$\begin{aligned} \int _{0}^{1}\!{\frac { \ln\left( x \right) ^{m-1}}{ {x}^{2}-1}}{dx}=& \left( -1 \right) ^{m-1}\int _{0}^{\infty }\!{\frac { {u}^{m-1}{{\rm e}^{-u}}}{-1+{{\rm e}^{-2\,u}}}}{du}\\ =&\left( -1 \right) ^{m-1} \int _{0}^{\infty }\!-{\frac {{u}^{m-1}}{-1+{{\rm e}^{u}}}}+{\frac {{u }^{m-1}}{-1+{{\rm e}^{2\,u}}}}{du}\\ =&\left( -1 \right) ^{m-1}\left( 1- \dfrac{1}{2^m} \right) \int _{0}^{\infty }\!{\frac {{u}^{m-1}}{-1+{{\rm e}^{u}}}}{du}\\ =&\left( -1 \right) ^{m}\left( 1- \dfrac{1}{2^m} \right) \Gamma \left( m \right) \zeta \left( m \right) \end{aligned}$$ where we have used Riemann's integral representation of the zeta function and we also made the substitution $u\rightarrow\frac{u}{2}$ in the second term of the second line to pass to line three (having noted that convergence of both terms individually is assured by comparison with Riemanns integral). It follows from $\Gamma(2)=1, \zeta(2)=\frac{\pi^2}{6}$ that: $$I(2)=\frac{\pi^2}{8}$$

Answer 3

We have$$\int_0^1\frac{\ln(x)}{x^2-1}\,\mathrm dx=\int_0^1\frac{\ln(1-x)}{(1-x)^2-1}\,\mathrm dx=\int_0^1\frac{\ln(1-x)}{x(x-2)}\,\mathrm dx$$ We will generalize by introducing parameter $\alpha$ such that $$I(\alpha )=\int_0^1\frac{\ln(1-\alpha x )}{x(x-2)}\,\mathrm dx$$ And we have $I(0)=0$ Then $$I'(\alpha )=-\int_0^1\frac{1}{(1-\alpha x)(x-2)}\,\mathrm dx=\frac{1}{2\alpha -1}\left[\ln\left(\frac{x-2}{1-\alpha x}\right)\right]_0^1=\frac{\ln(2-2\alpha )}{1-2\alpha }$$ And we have $$I'(\alpha )=\frac{\ln(2-2\alpha )}{1-2\alpha }$$

$$I(\alpha )=\frac{1}{2}\text{Li}_2(2\alpha -1)+c$$ $$I(0)=\frac{1}{2}\text{Li}_2(-1)+c=0\implies c=-\frac{1}{2}\text{Li}_2(-1)=\frac{\pi^2}{24}$$

$$I(\alpha )=\frac{1}{2}\text{Li}_2(2\alpha -1)+\frac{\pi^2}{24}$$ $$\begin{align}I(1)&=\frac{1}{2}\text{Li}_2(1)+\frac{\pi^2}{24}\\ &=\frac{\pi^2}{12}+\frac{\pi^2}{24}\\ &=\frac{\pi^2}{8}\\ \end{align}$$

$$I(1)=\int_0^1\frac{\ln(x)}{x^2-1}\,\mathrm dx=\frac{\pi^2}{8}$$

Answer 4

$\newcommand{\angles}[1]{\left\langle #1 \right\rangle}% \newcommand{\braces}[1]{\left\lbrace #1 \right\rbrace}% \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack}% \newcommand{\dd}{{\rm d}}% \newcommand{\isdiv}{\,\left.\right\vert\,}% \newcommand{\ds}[1]{\displaystyle{#1}}% \newcommand{\equalby}[1]{{#1 \atop {= \atop \vphantom{\huge A}}}}% \newcommand{\expo}[1]{\,{\rm e}^{#1}\,}% \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,}% \newcommand{\ic}{{\rm i}}% \newcommand{\imp}{\Longrightarrow}% \newcommand{\pars}[1]{\left( #1 \right)}% \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}}% \newcommand{\root}[2][]{\,\sqrt[#1]{\,#2\,}\,}% \newcommand{\sgn}{\,{\rm sgn}}% \newcommand{\ul}[1]{\underline{#1}}% \newcommand{\verts}[1]{\left\vert #1 \right\vert}% \newcommand{\yy}{\Longleftrightarrow}$

$$ {\cal I} \equiv \int_{0}^{1}{\ln\pars{x} \over x^{2} - 1}\,\dd x = \int_{1}^{\infty}{\ln\pars{x} \over x^{2} - 1}\,\dd x \quad\imp\quad {\cal I} \equiv {1 \over 2}\int_{0}^{\infty}{\ln\pars{x} \over x^{2} - 1}\,\dd x $$

Let's consider the integral $$ {\cal W} \equiv \int_{C}{\ln^{2}\pars{z} \over z^{2} - 1}\,\dd z = 0 $$ Then $\pars{~\mbox{with}\ z_{\pm} = x \pm \ic 0^{+}\ \mbox{and}\ z_{\pm}^{2} = x^{2} \pm \ic\sgn\pars{x}0^{+}~}$ \begin{align} &\int_{-\infty}^{0}{\bracks{\ln\pars{-x} + \ic\pi}^{2} \over z_{+}^{2} - 1}\,\dd x + \int_{0}^{-\infty}{\bracks{\ln\pars{-x} - \ic\pi}^{2} \over z_{-}^{2} - 1}\,\dd x \\[3mm]&= \sum_{\sigma = \pm 1}\sigma\int_{-\infty}^{0} {\ln^{2}\pars{-x} + 2\ic\pi\sigma\ln\pars{-x} - \pi^{2} \over x^{2} - 1 - \sigma\,\ic 0^{+}}\,\dd x \\[3mm]&= \sum_{\sigma = \pm 1}\sigma\,\braces{{\cal P}\int_{0}^{\infty} {\ln^{2}\pars{x} + 2\ic\pi\sigma\ln\pars{x} - \pi^{2} \over x^{2} - 1 }\,\dd x + \int_{0}^{\infty} {\bracks{\ln^{2}\pars{x} + 2\ic\pi\sigma\ln\pars{x} - \pi^{2}} \bracks{\ic\pi\sigma\delta\pars{x^{2} - 1}} }\,\dd x} \\[3mm]&= 4\pi\ic\int_{0}^{\infty}{\ln\pars{x} \over x^{2} - 1}\,\dd x + \pars{-\pi^{2}}2\pars{\ic\pi \over 2} = 0 \quad\imp\quad \int_{0}^{\infty}{\ln\pars{x} \over x^{2} - 1}\,\dd x = {\pi^{2} \over 4} \end{align} $${\large% {\cal I} = \int_{0}^{1}{\ln\pars{x} \over x^{2} - 1}\,\dd x = {\pi^{2} \over 8}} $$

Answer 5

Here is another way to solve. Using the substitute $u=x^2$ gives \begin{eqnarray} \int_0^1\frac{\ln x}{x^2-1}dx&=&-\frac{1}{4}\int_0^1\frac{\ln u}{(1-u)\sqrt u}dx\\ &=&-\frac14\lim_{\varepsilon\to0,\mu\to\frac12}\frac{\partial}{\partial \mu}\int_0^1(1-u)^{\varepsilon-1}u^{\mu-1}du\\ &=&-\frac14\lim_{\varepsilon\to0,\mu\to\frac12}\frac{\partial}{\partial \mu}B(\varepsilon,\mu)\\ &=&-\frac14\lim_{\varepsilon\to0,\mu\to\frac12}B(\varepsilon,\mu)(\psi(\mu)-\psi(\mu+\varepsilon))\\ &=&-\frac14\lim_{\varepsilon\to0,\mu\to\frac12}\frac{\Gamma(\varepsilon+\mu)}{\Gamma(\varepsilon)\Gamma(\mu)}(\psi(\mu)-\psi(\mu+\varepsilon))\\ &=&\frac14\lim_{\varepsilon\to0,\mu\to\frac12}\frac{\psi(\mu+\varepsilon)-\psi(\mu)}{\varepsilon}\frac{\varepsilon}{\Gamma(\varepsilon)}\frac{\Gamma(\varepsilon+\mu)}{\Gamma(\mu)}\\ &=&\frac{1}4\psi'(\frac{1}{2})\\ &=&\frac{\pi^2}{8}. \end{eqnarray} Here we used $$ \Gamma(\varepsilon)\approx\varepsilon \text{ for small }\varepsilon>0. $$

Answer 6

Write the integrand as a sum of fractions and use the polylogarithm function $\mathrm{Li}_2:$ $$f(x):=\int\frac{\ln(x)}{x^2-1}dx=\int\frac{1}{2}\left(\frac{\ln(x)}{x-1}- \frac{\ln(x)}{x+1}\right) dx \\ =\frac{1}{2} \int \frac{\ln(x) dx}{x-1}- \frac{1}{2} \int \frac{\ln(x)dx }{x+1} =-\frac{1}{2}\mathrm{Li}_2(1-x) -\frac{1}{2} \left(\mathrm{Li}_2(-x) + \ln(x)\ln(x+1)\right)$$ Since $\mathrm{Li}_2(0)=0$ and $\ln(x)\ln(x+1)$ vanishes at $x=0$ and $x=1$, we have $$f(0) = -\frac{1}{2}\mathrm{Li}_2(1)= -\frac{\pi^2}{12}$$ and $$f(1) = -\frac{1}{2}\mathrm{Li}_2(-1)= \frac{\pi^2}{24}$$ and the value of the integral is $$ \int_0^1\frac{\ln(x)}{x^2-1}dx=\frac{\pi^2}{24}+\frac{\pi^2}{12} = \frac{\pi^2}{8} $$

Answer 7

This comes from my answer here. Let

$$I = \int_0^{\infty} dx \frac{\log{x}}{x^2-1}$$

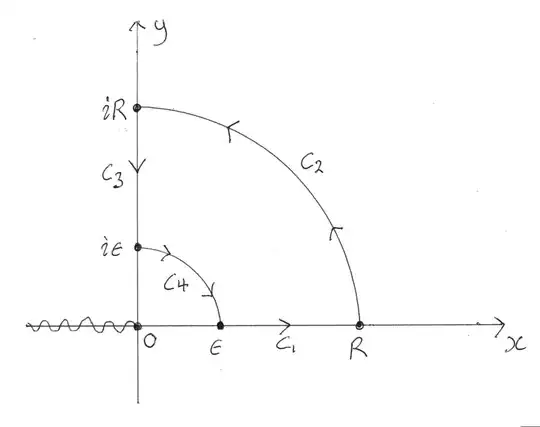
Note that the singularity at $x=1$ is removable in this integral and therefore we do not need to use a Cauchy principal value. We evaluate this integral by once again appealing to the residue theorem, but this time, we consider

$$\oint_{C'} dz \frac{\log^2{z}}{z^2-1}$$

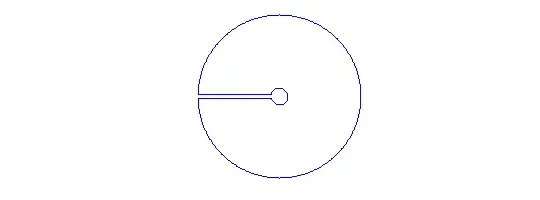
where $C'$ is a keyhole contour with respect to the positive real axis. By integrating around this contour and noting that the integrand vanishes sufficiently fast as the radius of the circular section of $C'$ increases without bound, we get

$$\oint_{C'} dz \frac{\log^2{z}}{z^2-1} = -i 4 \pi \int_0^{\infty} dx \frac{\log{x}}{x^2-1} + 4 \pi^2 \int_0^{\infty} dx \frac{1}{x^2-1}$$

This is equal to, by the residue theorem, $i 2 \pi$ times the sum of the residues of the poles of the integrand of the complex integral within $C'$. As the only pole is at $z=-1$, we see that

$$\begin{align}\oint_{C'} dz \frac{\log^2{z}}{z^2-1} &= i 2 \pi \frac{\log^2{(-1)}}{2 (-1)} \\ &= i 2 \pi \frac{\pi^2}{2}\end{align}$$

Now, the real part of the integral above is split into a Cauchy principal value and a piece indented about the singularity at $x=1$. The Cauchy principal value is zero:

$$\begin{align}PV \int_0^{\infty} dx \frac{1}{x^2-1} &= \lim_{\epsilon \rightarrow 0} \left [\int_0^{1-\epsilon} dx \frac{1}{x^2-1} + \int_{1+\epsilon}^{\infty} dx \frac{1}{x^2-1}\right]\\ &= \lim_{\epsilon \rightarrow 0} \left [\int_0^{1-\epsilon} dx \frac{1}{x^2-1} + \int_0^{1/(1+\epsilon)} \left (-\frac{dx}{x^2} \right ) \frac{1}{(1/x^2)-1} \right ]\\ &= \lim_{\epsilon \rightarrow 0} \left [\int_0^{1-\epsilon} dx \frac{1}{x^2-1} - \int_0^{1-\epsilon} \frac{dx}{x^2-1} \right ] \\ &= 0\end{align}$$

The indent in the contour, however, produces a contribution; let $x=1+\epsilon e^{i \phi}$ and $\phi \in [\pi,0]$:

$$4 \pi^2 i \epsilon \int_{-\pi}^0 d\phi \frac{e^{i \phi}}{2 \epsilon e^{i \phi}} = i \frac{\pi}{2} 4 \pi^2$$

so that

$$-i 4 \pi \int_0^{\infty} dx \frac{\log{x}}{x^2-1} = i 2 \pi \frac{\pi^2}{2} - i \frac{\pi}{2} 4 \pi^2 = -i 2 \pi \frac{\pi^2}{2}$$

Therefore

$$I = \int_0^{\infty} dx \frac{\log{x}}{x^2-1} = \frac{\pi^2}{4}$$

But the sought-after integral is

$$\int_0^{1} dx \frac{\log{x}}{x^2-1} = \frac12 I = \frac{\pi^2}{8}$$

Answer 8

Let $ I(a)= \int_0^1 \frac{\ln (1+x^2+(1-x^2)\cos a)}{x^2-1}\ dx$. Then, $I’(a)=\frac a2$ \begin{align}\int_0^1\frac{\ln x}{x^2-1}\,dx= &\ \frac12\int_0^\pi I’(a)da = \frac14 \int_0^\pi ada=\frac{\pi^2}{8} \end{align}

Answer 9

Feynman’s Trick

Let $$ I(\theta)=\int_0^1 \frac{\ln \left[1+\sin ^2 \theta\left(t^2-1\right)\right]}{t^2-1} d t $$ Differentiating $I(\theta)$ w.r.t. $\theta$ yields $$ \begin{aligned} I^{\prime}(\theta) & =\int_0^1 \frac{2 \sin \theta \cos \theta}{\cos ^2 \theta+t^2\sin ^2 \theta} d t \\ & =\frac{2 \sin \theta \cos \theta}{\sin \theta \cos \theta}\left[\tan ^{-1}(t \tan \theta)\right]_0^1 \\ & =2 \theta \end{aligned}$$ Integrating back gives $$ \begin{aligned} \begin{aligned} \int_0^1 \frac{\ln \left(t^2\right)}{t^2-1} d \theta & =\int_0^{\frac{\pi}{2}} I^{\prime}(\theta) d \theta \\ & =\int_0^{\frac{\pi}{2}} 2 \theta d \theta \\ & =[\theta^2]_0^{ \frac{ \pi}{2} } \\ & =\frac{\pi^2}{4} \end{aligned}\end{aligned} $$

Hence $$\boxed{\int_0^1 \frac{\ln \left(t\right)}{t^2-1} d t =\frac{\pi^2}{8}} $$

Answer 10

While there are already answers here that utilize complex contour integration, my approach may offer a simpler alternative.

The substitution $x \rightarrow 1/x$ gives:

\begin{align} \int_0^1 \frac{\ln x}{1-x^2} dx & = \int_\infty^1 \frac{\ln (1/x)}{1-(1/x^2)} \cdot - \frac{1}{x^2} dx \nonumber \\ & = \int_1^\infty \frac{\ln x}{1-x^2} dx \end{align}

Therefore,

\begin{align} \int_0^1 \frac{\ln x}{1-x^2} dx & = \frac{1}{2} \int_0^\infty \frac{\ln x}{1-x^2} dx \end{align}

We evaluate the integral on the RHS via contour integration. We cut the plane along $( \infty , 0 ]$ and take the holomorphic branch of the logarithm given by $\ln z = \ln |z| + i \theta$, where $z=|z|e^{i \theta}$ and $-\pi < \theta < \pi$. Consider the function $f(z) = \ln z / (1-z^2)$. L'Hôpital's Rule tells us the limit $z \rightarrow 1$ in $\ln z / (1-z^2)$ exists and is finite. Consider the contour:

Then

\begin{align} \int_\epsilon^R \frac{\ln x}{1-x^2} dx + \int_{C_2} f(z) dz + \int_R^\epsilon \frac{\ln x + i \pi/2}{1+x^2} (-idx) + \int_{C_4} f(z) dz = 0 \qquad (1) \end{align}

Estimates:

\begin{align} \left| \int_{C_2} f(z) \right| & \leq \int_0^{\pi/2} \left| \frac{\ln R + i \theta}{1-R^2 e^{2i \theta}} Ri e^{i \theta} \right| d \theta \nonumber \\ & \leq \int_0^{\pi/2} \frac{(\ln R + \pi)R}{R^2-1} d \theta = \mathcal{O} (R^{-1} \ln R) \end{align}

and

\begin{align} \left| \int_{C_4} f(z) \right| & \leq \int_0^{\pi/2} \left| \frac{\ln \epsilon + i \theta}{1-\epsilon^2 e^{2i \theta}} \epsilon i e^{i \theta} \right| d \theta \nonumber \\ & \leq \int_0^{\pi/2} \frac{(|\ln \epsilon| + \pi)\epsilon}{1-\epsilon^2} d \theta = \mathcal{O} (\epsilon \ln \epsilon) \end{align}

So in the limit $R \rightarrow \infty, \epsilon \rightarrow 0$ in (1) gives:

\begin{align} \int_0^\infty \frac{\ln x}{1-x^2} dx & = -i \int_0^\infty \frac{\ln x}{1+x^2} dx - \frac{\pi}{2} \int_0^\infty \frac{dx}{1+x^2} \nonumber \\ & = - \frac{\pi^2}{4} \end{align}

Hence

\begin{align} \int_0^1 \frac{\ln x}{x^2-1} dx & = \frac{\pi^2}{8} \end{align}

Answer 11

Here is a Feynman-integral-trick approach, with rigorous derivation. Consider for $a>0$ $$ I(a):=\int_{x=0}^1\frac{\ln(1+a^2x^2)-\ln(1+a^2)}{x^2-1}\,dx\tag1 $$ which, by partial fraction decomposition of the integrand, equals $$ \int_{x=0}^1\left(\int_{t=0}^a\frac{2t}{(1+t^2x^2)(1+t^2)}\,dt\right)\,dx. $$ Interchange order of integration to find $$ I(a)=\int_{t=0}^a\frac{2}{1+t^2}\left(\int_{x=0}^1\frac{t\,dx}{1+t^2x^2}\right)\,dt =\int_{t=0}^a\frac{2\arctan(t)\,dt}{1+t^2} =\int_{u=0}^{\arctan a}2u\,du=(\arctan a)^2. $$ The integrand in $(1)$ is non-negative and increases to $\displaystyle\frac{\ln(x^2)}{x^2-1}$ as $a\to\infty$. So by monotone convergence, it is legal to interchange the limit and integration operations, obtaining $$ \int_{x=0}^1\frac{\ln (x^2)}{x^2-1}\,dx=\lim_{a\to\infty}I(a)=\left(\frac\pi2\right)^2.$$

Answer 12

I will provide a solution using hyperbolic functions which are often overlooked, but sometimes are of great help.

Substitute $x=\tanh t$:

$$\begin{align}\int_0^1\ln\coth t\,\mathrm dt&=\int_0^1\int_0^1\frac{y}{\cosh^22x-y^2}\mathrm dy\,\mathrm dx\\&=\int_0^1\int_0^1\frac{y\operatorname{sech}^22x}{y^2\tanh^22x+1-y^2}\mathrm dx\,\mathrm dy\\&=\frac\pi4\int_0^1\frac{\mathrm dy}{\sqrt{1-y^2}}\\&=\frac{\pi^2}8\end{align}$$

Answer 13

Following the initial part of @Graham Hesketh's idea,

\begin{align} \int_0^1 \frac{\ln x}{x^2-1} dx & = - \int_0^\infty \frac{u e^{-u}}{e^{-2u}-1} du \nonumber \\ & = - \int_0^\infty \frac{u}{e^u-1} du + \int_0^\infty \frac{u}{e^{2u}-1} du \nonumber \\ & = \left( 1 - \frac{1}{2^2} \right) \int_0^\infty \frac{u}{e^u-1} du \nonumber \\ & = \frac{3}{8} \int_0^\infty \frac{u^2 e^u}{(e^u-1)^2} du \qquad (*) \end{align}

where in the last step I have integrated by parts. Consider

\begin{align*} \int_0^\infty \frac{u^2 e^x}{(e^u-1)^2} du - \int_0^\infty \frac{u^2 e^u}{(e^u+1)^2} du & = \int_0^\infty \frac{4 u^2 e^{2u}}{(e^{2u}-1)^2} du \nonumber \\ & = \frac{1}{2} \int_0^\infty \frac{u^2 e^u}{(e^u-1)^2} du \end{align*}

which rearranged gives

\begin{align*} \int_0^\infty \frac{u^2 e^u}{(e^u-1)^2} = 2 \int_0^\infty \frac{u^2 e^u}{(e^u+1)^2} du \end{align*}

Substituting this into $(*)$ gives

\begin{align} \int_0^1 \frac{\ln x}{x^2-1} dx & = \frac{3}{4} \int_0^\infty \frac{u^2 e^u}{(e^u+1)^2} du \end{align}

Here I evaluated the integral on the RHS via complex contour integration obtaining: $\int_0^\infty \frac{u^2 e^u}{(e^u+1)^2} du = \frac{\pi^2}{6}$. The integral $\int_0^\infty \frac{u^2 e^u}{(e^u-1)^2} du$ does not seem amenable to this method, which is why I rewrote it using the derived identity. So finally,

\begin{align} \int_0^1 \frac{\ln x}{x^2-1} dx & = \frac{\pi^2}{8} . \end{align}

EDIT: In the link above, I am considering a more general case. The specific integral $\int_0^\infty \frac{u^2 e^u}{(e^u+1)^2} du$ can easily be evaluated using contour integration of the function $f(z) = \frac{z^3 e^z}{(e^z+1)^2}$ around the contour discussed in the aforementioned link. Alternatively, the integral $\int_0^\infty \frac{u}{e^u-1} du$ can be evaluated via contour integration by considering the function $\frac{z^2}{e^z-1}$ as shown by @Max0815 here