Find integral $\int_0^1 \frac{\ln x}{1 - x^2} \mathrm{d}x$

Question

I have to find definite integration $$\int_0^1 \frac{\ln x}{1 - x^2} \mathrm{d}x$$ I tried to subtitute $x = \sin u$ and $x = e^u$ but got no result . Please help me in proceeding.

Answer 1

$$\int_0^1 \frac{\ln x}{1 - x^2} \mathrm{d}x$$

Note that for $|x|<1$:

$$\sum_{n=0}^{\infty} x^{n}=\frac{1}{1-x}$$

Hence for $|x^2|<1$:

$$\sum_{n=0}^{\infty} x^{2n}=\frac{1}{1-(x^2)}$$

So we get:

$$=\int_{0}^{1} \sum_{n=0}^{\infty} x^{2n}\log x dx$$

$$=\sum_{n=0}^{\infty} \int_{0}^{1} x^{2n} \log x dx$$

Integration by parts.

$$=\sum_{n=0}^{\infty} -\frac{1}{(2n+1)^2}$$

$$=-\sum_{n=1}^{\infty} \frac{1}{(2n-1)^2}$$

Now think about evens and odds to see that this is equivalently:

$$=-\left( \sum_{n=1}^{\infty} \frac{1}{n^2}-\sum_{n=1}^{\infty} \frac{1}{(2n)^2}\right)$$

$$=-\frac{3}{4} \sum_{n=1}^{\infty} \frac{1}{n^2}$$

Answer 2

Let $I(a) =\dfrac12 \displaystyle \int_0^1 \dfrac1{1 - x^2}\,\ln \dfrac{1+a^2x^2}{1+a^2}\, dx,$ to have $I’(a)=-\dfrac{\tan^{-1}a}{1+a^2}.$ Then

\begin{align} \int_0^1 \frac{\ln x}{1 - x^2}{d}x & = \int_0^\infty I’(a)da = -\int_0^\infty \frac{\tan^{-1}a}{1+a^2}da =-\frac{\pi^2}8. \end{align}

Answer 3

The substitution

$$x = e^u$$

is perfect, if you know how to proceed.

$$x = e^u ~~~~~ \text{d}x = e^{u}\ \text{d}u$$

Hence you get

$$\int_{-\infty}^0 \frac{u e^{u}}{1 - e^{2u}}\ \text{d}u$$

We recognize the possibility to use the Geometric Series with the fraction

$$\frac{1}{1 - e^{2u}} = \sum_{k = 0}^{+\infty} e^{2uk}$$

So

$$\int_{-\infty}^0\ ue^{u}\ \sum_{k = 0}^{+\infty} e^{2uk}\ \text{d}u = \sum_{k = 0}^{+\infty}\int_{-\infty}^0\ u\ e^{u(1 + 2k)}\ \text{d}u$$

Now the integration is trivial if you compute it by parts with

$$f = u ~~~~~ g' = e^{u(1 + 2k)}$$

Integrating by parts one and you get finally

$$\sum_{k = 0}^{+\infty} \frac{-1}{(1 + 2k)^2} = -\frac{\pi^2}{8}$$

By parts calculation

$$\int_{-\infty}^0\ u\ e^{u(1 + 2k)}\ \text{d}u = \frac{u}{1+2k}e^{u(1+2k)}\bigg|_{-\infty}^0 - \int_{-\infty}^0\ \frac{e^{u(1 + 2k)}}{1+2k}\ \text{d}u$$

The first term is zero, hence you need to evaluate the trivial integral

$$ - \int_{-\infty}^0\ \frac{e^{u(1 + 2k)}}{1+2k}\ \text{d}u = -\frac{1}{(1+2k)^2}e^{u(1+2k)}\bigg|_{-\infty}^0 = \frac{-1}{(1+2k)^2}$$

Answer 4

The first step is to turn the one integral into two as follows: \begin{align} \int_{0}^{1} \frac{\ln(x)}{1-x^2} \, dx = \frac{1}{2} \, \left[ \int_{0}^{1} \frac{\ln(x)}{1-x} \, dx + \int_{0}^{1} \frac{\ln(x)}{1+x} \, dx \right] \end{align} then using the integrals \begin{align} \int_{0}^{1} \frac{\ln(x)}{1-x} \, dx &= \left[\operatorname{Li}_{2}(1-x) \right]_{0}^{1} = - \zeta(2) = - \frac{\pi^2}{6} \\ \int_{0}^{1} \frac{\ln(x)}{1+x} \, dx &= - \frac{\pi^2}{12} \end{align} the desired integral becomes $$\int_{0}^{1} \frac{\ln(x)}{1-x^2} \, dx = - \frac{\pi^2}{8}.$$

Answer 5

$\newcommand{\angles}[1]{\left\langle\,{#1}\,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{\mathrm{i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\Li}[1]{\,\mathrm{Li}_{#1}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ Hereafter, $\ds{\Psi}$ is the Digamma Function: \begin{align} & \color{#f00}{\int_{0}^{1}{\ln\pars{x} \over 1 - x^{2}}\,\dd x} = \left.\partiald{}{\mu}\int_{0}^{1}{x^{\mu} - 1 \over 1 - x^{2}}\,\dd x \,\right\vert_{\ \mu\ =\ 0} \\[5mm] & \stackrel{x\ \to\ x^{1/2}}{=}\,\,\,\,\, \left.\half\,\partiald{}{\mu} \int_{0}^{1}{x^{\mu/2 - 1/2}\,\,\,\, -\,\, x^{-1/2} \over 1 - x}\,\dd x \,\right\vert_{\ \mu\ =\ 0} \\[5mm] & = \half\,\partiald{}{\mu} \bracks{\Psi\pars{\half} - \Psi\pars{{\mu \over 2} + \half}}_{\ \mu\ =\ 0} \\[5mm] & = -\,{1 \over 4}\,\Psi\,'\pars{\half} = -\,{1 \over 4}\sum_{k = 0}^{\infty}{1 \over \pars{k + 1/2}^{2}} \\[5mm] = & \ -\sum_{k = 0}^{\infty}{1 \over \pars{2k + 1}^{2}} = -\sum_{k = 0}^{\infty}{1 \over k^{2}} + \sum_{k = 0}^{\infty}{1 \over \pars{2k}^{2}} \\[5mm] = & \ -\,{3 \over 4}\ \underbrace{\sum_{k = 0}^{\infty}{1 \over k^{2}}}_{\ds{\pi^{2} \over 6}}\ =\ {\Large\color{#f00}{-\,{\pi^{2} \over 8}}} \end{align}

Answer 6

The substitution $x \rightarrow 1/x$ gives:

\begin{align} \int_0^1 \frac{\ln x}{1-x^2} dx & = \int_\infty^1 \frac{\ln (1/x)}{1-(1/x^2)} \cdot - \frac{1}{x^2} dx \nonumber \\ & = \int_1^\infty \frac{\ln x}{1-x^2} dx \end{align}

Therefore,

\begin{align} \int_0^1 \frac{\ln x}{1-x^2} dx & = \frac{1}{2} \int_0^\infty \frac{\ln x}{1-x^2} dx \end{align}

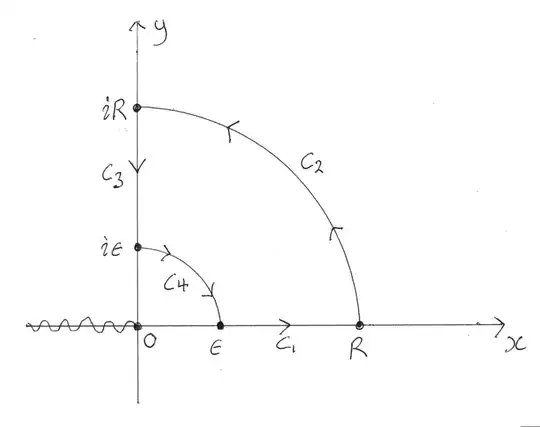
We evaluate the integral on the RHS via contour integration. We cut the plane along $( \infty , 0 ]$ and take the holomorphic branch of the logarithm given by $\ln z = \ln |z| + i \theta$, where $z=|z|e^{i \theta}$ and $-\pi < \theta < \pi$. L'Hôpital's Rule tells us the limit $z \rightarrow 1$ in $\ln z / (1-z^2)$ exists and is finite. Consider the contour:

Then

\begin{align} \int_\epsilon^R \frac{\ln x}{1-x^2} dx + \int_{C_2} f(z) dz + \int_R^\epsilon \frac{\ln x + i \pi/2}{1+x^2} (-idx) + \int_{C_4} f(z) dz = 0 \qquad (1) \end{align}

Estimates:

\begin{align} \left| \int_{C_2} f(z) \right| & \leq \int_0^{\pi/2} \left| \frac{\ln R + i \theta}{1-R^2 e^{2i \theta}} Ri e^{i \theta} \right| d \theta \nonumber \\ & \leq \int_0^{\pi/2} \frac{(\ln R + \pi)R}{R^2-1} d \theta = \mathcal{O} (R^{-1} \ln R) \end{align}

and

\begin{align} \left| \int_{C_4} f(z) \right| & \leq \int_0^{\pi/2} \left| \frac{\ln \epsilon + i \theta}{1-\epsilon^2 e^{2i \theta}} \epsilon i e^{i \theta} \right| d \theta \nonumber \\ & \leq \int_0^{\pi/2} \frac{(|\ln \epsilon| + \pi)\epsilon}{1-\epsilon^2} d \theta = \mathcal{O} (\epsilon \ln \epsilon) \end{align}

So in the limit $R \rightarrow \infty, \epsilon \rightarrow 0$ in (1) gives:

\begin{align} \int_0^\infty \frac{\ln x}{1-x^2} dx & = -i \int_0^\infty \frac{\ln x}{1+x^2} dx - \frac{\pi}{2} \int_0^\infty \frac{dx}{1+x^2} \nonumber \\ & = - \frac{\pi}{4} \end{align}

Hence

\begin{align} \int_0^1 \frac{\ln x}{1-x^2} dx & = - \frac{\pi}{8} \end{align}

Answer 7

$$\int_0^\infty\frac{\ln x}{1-x^2}dx\stackrel{x=e^{-t}}{=}-\int_0^\infty\frac{te^{-t}}{1-e^{-2t}}dt\stackrel{t=\frac x2}{=}-\frac14\int_0^\infty\frac{x^{\color{blue}{2}-1}e^{-\color{red}{\frac12x}}}{1-e^{-x}}dx=-\frac14\zeta(2,\frac12)$$ where by definition of Hurtwitz zeta function, $$\zeta(2,\frac12)=\sum_{n=0}^\infty\frac1{(n+\frac12)^2}=4\sum_{n=0}^\infty\frac1{(2n+1)^2}=4\sum_{n=1}^\infty\frac1{n^2}-4\sum_{n=1}^\infty\frac1{(2n)^2}=(4-1)\sum_{n=1}^\infty\frac1{n^2}=3\zeta(2)=\frac{\pi^2}{2}.$$