How to evaluate $\int_{-\infty}^{\infty}dx \frac{x^2 e^x}{(e^x+1)^2}$

Question

My physics textbook makes use of the result: $$\int_{-\infty}^{\infty}dx \dfrac{x^2 e^x}{(e^x+1)^2} = \dfrac{\pi^2}{3}$$ I'm really curious on how I can derive this but I honestly don't know what to search for. My instinct is to transform to polar coordinates but I would like some guidance. Any help appreciated!

Answer 1

First off, notice the integrand is even, so we have $$ \int_{-\infty}^\infty \frac{x^2 e^x}{(e^x+1)^2}dx = 2\int_{0}^\infty \frac{x^2 e^x}{(e^x+1)^2}dx.$$ Then we can expand $$ \frac{1}{(1+x)^2} = \sum_{n=0}^\infty (-1)^{n}(n+1) x^n $$ and write $$ 2\int_{0}^\infty \frac{x^2 e^x}{(e^x+1)^2}dx=\\ =2\int_{0}^\infty \frac{x^2 e^{-x}}{(e^{-x}+1)^2}dx \\ = 2 \int_0^\infty x^2e^{-x}\sum_{n=0}^\infty (-1)^n (n+1) e^{-nx}\\=2\sum_{n=0}^\infty (-1)^n(n+1) \int_0^\infty x^2 e^{-(n+1)x}dx\\=4\sum_{n=0}^\infty \frac{(-1)^n}{(n+1)^2}.$$ Then we have $$ \sum_{n=0}^\infty \frac{(-1)^n}{(n+1)^2} = 1-\frac{1}{2^2} + \frac{1}{3^2}\ldots = (1-\frac{2}{2^2})(1+\frac{1}{2^2} + \frac{1}{3^2}\ldots) = \frac{\pi^2}{12}$$

Edit Realized this can be simplified somewhat by first doing an integration by parts $$ 2\int_0^\infty \frac{x^2 e^x}{(e^x+1)^2}dx = 4\int_0^\infty \frac{x}{e^x+1}dx$$ followed by a similar series expansion. Additionally, this solution somewhat 'misses the point' relative to contour integration approaches since that's one of the slicker ways to get $\sum_{n}1/n^2=\pi^2/6$ in the first place (and also transformation from the sums to integrals like this are the source of many zeta function identities).

Answer 2

Substitute $e^x=t$ we get $$I=\int_0^{\infty} \frac {\ln^2t dt}{(1+t)^2}$$

Let $$J(a)=\int_0^{\infty} \frac {t^{a-1}dt}{(1+t)^2}$$

So we need to find $J''(1)$

Notice that $$J(a)=B(a,2-a)=\frac {\Gamma(a)\Gamma(2-a)}{\Gamma(2)}$$

Where $B(x,y)$ is Standard beta function and $\Gamma(x)$ is the Gamma function

Using the properties of Gamma function and Euler's reflection formula we have $$J(a)=\Gamma(a) \cdot(1-a)\Gamma(1-a)=\pi \frac {1-a}{\sin \pi a}$$

Differentiating twice w.r.t $a$ and taking limit $a\to 1$ gives the desired result

Answer 3

You have $$ \int_{-\infty}^\infty\frac{x^2 e^x}{(e^x+1)^2}\,\mathrm{d}x= \int_{-\infty}^\infty\frac{x^2}{2(\cosh x+1)}\,\mathrm{d}x $$ So integrate $\dfrac{z^3}{1+\cosh z}$ around rectangle $\pm R\pm2\pi i$, we have encircled a simple pole at $\pi i$ with residue $6\pi^2$. The vertical sides contribution is $\to 0$ as $R\to\infty$ because of cosh in the denominator, and the horizontal contribution $$ \int_{-\infty}^\infty\frac{x^3}{1+\cosh x}\,\mathrm{d}x+\int_\infty^{-\infty}\frac{(x+2\pi i)^3}{1+\underbrace{\cosh(x+2\pi i)}_{=\cosh x}}\,\mathrm{d}x $$ whose imaginary part is $$ 2\pi\int_\infty^{-\infty}\frac{3x^2-4\pi^2}{1+\cosh(x)}\,\mathrm{d}x. $$ So $$ 3\int_\infty^{-\infty}\frac{x^2}{1+\cosh(x)}\,\mathrm{d}x -4\pi^2\int_\infty^{-\infty}\frac{1}{1+\cosh(x)}\,\mathrm{d}x =6\pi^2 $$ i.e., \begin{align} \int_{-\infty}^\infty\frac{x^2}{2(1+\cosh(x))}\,\mathrm{d}x &=-\pi^2 +\frac43\pi^2\int_{-\infty}^\infty\frac{1}{2(1+\cosh(x))}\,\mathrm{d}x \\ &=-\pi^2+\frac43\pi^2=\frac13\pi^2 \end{align} since $$ \int_{-\infty}^\infty\frac{1}{2(\cosh x+1)}\,\mathrm{d}x=\int_{-\infty}^\infty\frac14\operatorname{sech}^2\frac x2\,\mathrm{d}x=\left[\frac12\tanh\frac x2\right]_{-\infty}^\infty=1. $$

Answer 4

Here we use Feynman's Trick to facilitate analysis. Proceeding, we have

$$\begin{align} I&=\int_{-\infty}^\infty \frac{x^2e^x}{(e^x+1)^2}\,dx\\\\ &=2\int_0^\infty \frac{x^2e^x}{(e^x+1)^2}\,dx\\\\ &=-2\left.\left(\frac{d}{dy}\int_0^\infty \frac{x^2}{ye^x+1}\,dx\right)\right|_{y=1}\\\\ &=-2\left.\left(\frac{d}{dy}\int_0^\infty \frac{x^2e^{-x}}{e^{-x}+y}\,dx\right)\right|_{y=1}\\\\ &=-2\left.\frac{d}{dy}\left(\frac1y\int_0^\infty \frac{x^2e^{-x}}{e^{-x}/y+1}\,dx\right)\right|_{y=1}\\\\ &=-2\left.\frac{d}{dy}\left(\sum_{n=0}^\infty \frac{(-1)^n}{y^{n+1}}\int_0^\infty x^2e^{-(n+1)x}\,dx\right)\right|_{y=1}\\\\ &=-4\left.\frac{d}{dy}\left(\sum_{n=0}^\infty \frac{(-1)^n}{y^{n+1}(n+1)^3}\right)\right|_{y=1}\\\\ &=4\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^2}\\\\ &=4\frac{\pi^2}{12}\\\\ &=\frac{\pi^2}3 \end{align}$$

Answer 5

my first thought was trying substitution: $$I=\int_{-\infty}^\infty\frac{x^2e^x}{(e^x+1)^2}dx$$ $u=e^x+1,\,dx=\frac{du}{e^x}$ $$I=\int_1^\infty\frac{x^2}{u^2}du=\int_1^\infty\frac{\ln^2(u-1)}{u^2}du$$ if we now let: $$I(a)=\int_1^\infty\frac{\ln(au-1)}{u^2}du$$ then: $$I''(a)=\int_1^\infty\ln(au-1)du$$ $v=au-1,\,du=\frac{dv}{a}$ $$I''(a)=\frac1a\int_a^\infty\ln(v)dv$$ although this leaves us with a divergent integral, which does not help.

Another approach: $$I=\int_{-\infty}^\infty\frac{x^2e^x}{(e^x+1)^2}dx=\int_{-\infty}^\infty\frac{x^2[(e^x+1)-1]}{(e^x+1)^2}dx=\int_{-\infty}^\infty\frac{x^2}{e^x+1}dx-\int_{-\infty}^\infty\frac{x^2}{(e^x+1)^2}dx$$

Answer 6

The integral you are interested in can be rewritten in the form: $$\int_{-\infty}^{\infty}\frac{x^{2}}{2\ cosh(x)+2} dx$$

Several techniques for solving integrals similar to this can be found at:

Improper Integral of $x^2/\cosh(x)$

Answer 7

One of the standard solutions for evaluating difficult integrals is to transform the integrand into an infinite sequence and then integrating termwise. Indeed, if we start off with the geometric sum$$\sum\limits_{n\geq0}x^n=\frac 1{1-x}$$multiply both sides by $x$ and differentiating with respect to $x$, it's easy to see that$$\sum\limits_{n\geq0}(n+1)x^n=\frac 1{(1-x)^2}$$Replace $x$ with $-e^{-x}$ in the problem and calling the integral $\mathfrak{I}$, the problem transforms into$$\begin{align*}\mathfrak{I} & =2\sum\limits_{n\geq0}(-1)^n(n+1)\int\limits_{0}^{\infty}\mathrm dx\,x^2 e^{-(n+1)x}\end{align*}$$The remaining integral can be evaluated using integration by parts on $u=x^2$ to get$$\mathfrak I=4\sum\limits_{n\geq0}\frac {(-1)^{n}}{(n+1)^2}=4\sum\limits_{n\geq1}\frac {(-1)^{n-1}}{n^2}$$The inner sum is equal to $\pi^2/12$ and is due to the identity$$\eta(s)=(1-2^{1-s})\zeta(s)$$Where$$\eta(s)=\sum\limits_{n\geq1}\frac {(-1)^{n-1}}{n^s}$$$$\zeta(s)=\sum\limits_{n\geq1}\frac 1{n^s}$$Since $\zeta(2)=\pi^2/6$, the result follows immediately$$\int\limits_{-\infty}^{\infty}\mathrm dx\,\frac {x^2e^{x}}{(1+e^x)^2}\color{blue}{=\frac {\pi^2}{3}}$$

Answer 8

We could even compute the antiderivative since $$I=\int\frac{x^2 e^x}{(e^x+1)^2}\,dx=x \left(\frac{e^x x}{e^x+1}-2 \log \left(e^x+1\right)\right)-2 \text{Li}_2\left(-e^x\right)$$ making $$J=\int_0^p\frac{x^2 e^x}{(e^x+1)^2}\,dx=\frac{e^p p^2}{e^p+1}-2 \text{Li}_2\left(-e^p\right)-2 p \log \left(e^p+1\right)-\frac{\pi ^2}{6}$$ Expanding as series for large values of $p$ $$J=\left(2-\frac{1}{e^p+1}\right) p^2+\frac{1}{2} e^{-2 p} \left(1-4 e^p\right)+\frac{\pi ^2}{6}-2 p \log \left(e^p+1\right)+\cdots$$ which shows the limit and which is a quite good approximation even for small values of $p$ $$\left( \begin{array}{ccc} p & \text{approximation} & \text{exact} \\ 1 & 0.08137802971721 & 0.07217327763488 \\ 2 & 0.39889758755901 & 0.39838536515902 \\ 3 & 0.82824233816028 & 0.82821565813003 \\ 4 & 1.17549173764877 & 1.17549038617232 \\ 5 & 1.39700611481663 & 1.39700604709488 \\ 6 & 1.52125697930945 & 1.52125697592972 \\ 7 & 1.58570867980301 & 1.58570867963459 \\ 8 & 1.61743428754382 & 1.61743428753543 \\ 9 & 1.63247105478514 & 1.63247105478472 \\ 10 & 1.63939550316470 & 1.63939550316468 \end{array} \right)$$

Answer 9

Consider the integral:

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^{x} + 1)^2} dx \end{align*}

where $-\frac{1}{2} \leq \alpha \leq \frac{1}{2}$. Then

\begin{align*} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x + 1)^2} dx = \left. \dfrac{\partial^{2k}}{\partial \alpha^{2k}} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^{x} + 1)^2} dx \right|_{\alpha=0} \end{align*}

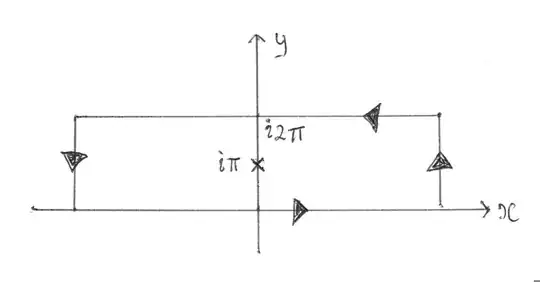
We evaluate this integral using a contour integral. Consider the rectangular contour, $C$, in the figure

and integral

\begin{align*} \oint_C \dfrac{e^{\alpha z} e^z}{(e^z + 1)^2} dz \end{align*}

whose integrand has pole at $\pi i$. The integral along the vertical edges vanishes as:

\begin{align*} f(z) = \dfrac{e^{\alpha (x+iy)} e^{(x+iy)}}{(e^{x+iy} + 1)^2} = \begin{cases} e^{- (1 - \alpha) (x+iy)} & x \rightarrow \infty \\ e^{(1 + \alpha) (x+iy)} & x \rightarrow - \infty \\ \end{cases} \end{align*}

So that

\begin{align*} \oint_C \dfrac{e^{\alpha z} e^z}{(e^z + 1)^2} dz & = \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x - 1)^2} dx - e^{i 2 \alpha \pi} \int_{-\infty + i 2 \pi}^{\infty + i 2 \pi} \dfrac{e^{\alpha x} e^x}{(e^x - 1)^2} dx \nonumber \\ & = (1 - e^{i 2 \alpha \pi}) \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} dx \end{align*}

Which rearranged is

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} dx & = \frac{2 \pi i}{1 - e^{i 2 \alpha \pi}} \frac{1}{2 \pi i} \oint_C \dfrac{e^{\alpha z} e^z}{(e^z + 1)^2} dz \nonumber \\ & = \frac{2 \pi i}{1 - e^{i 2 \alpha \pi}} Res_{z=\pi i} [f(z)] . \end{align*}

We now obtain the residue. We wish to expand the integrand in powers of $z-z_0$ about pole $z_0 = i \pi$. First note:

\begin{align*} \frac{1}{(e^z + 1)^2} & = \frac{1}{(e^{z_0 + (z-z_0)} - e^{z_0})^2} \nonumber \\ & = e^{-2 z_0} \dfrac{1}{[(z-z_0) + \frac{1}{2!} (z-z_0)^2+ \cdots]^2} \nonumber \\ & = \dfrac{1}{(z-z_0)^2 [(1 + \frac{1}{2!} (z-z_0)+ \cdots]^2} \nonumber \\ & = \dfrac{1}{(z-z_0)^2 [1 + (z-z_0) + \cdots]} \nonumber \\ & = \dfrac{1}{(z-z_0)^2} [(1 - (z-z_0) + \cdots] \nonumber \\ & = \dfrac{1}{(z-z_0)^2} - \dfrac{1}{z-z_0} + \cdots \end{align*}

Using this we have:

\begin{align*} \frac{e^{\alpha z} e^z}{(e^z + 1)^2} & = \dfrac{ e^{(\alpha + 1) z_0 + (\alpha + 1) (z-z_0)} }{ (z-z_0)^2 } - \dfrac{ e^{(\alpha + 1) z_0} }{ z-z_0 } + \cdots \nonumber \\ & = \dfrac{ e^{(\alpha + 1) z_0} [1 + (\alpha + 1) (z-z_0) + \cdots] }{ (z-z_0)^2 } - \dfrac{ e^{(\alpha + 1) z_0} }{ z-z_0 } + \cdots \nonumber \\ & = \dfrac{ e^{(\alpha + 1) z_0} }{ (z-z_0)^2 } + \dfrac{ \alpha e^{(\alpha + 1) z_0} }{ z-z_0 } + \cdots \end{align*}

From which we can read off the residue. So that

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} dx & = \frac{2 \pi i}{1 - e^{i 2 \alpha \pi}} \cdot \alpha e^{i (\alpha + 1) \pi} \nonumber \\ & = \frac{\alpha \pi}{\sin( \alpha \pi)} . \end{align*}

We have the series expansion of $x \pi \csc x \pi$ in terms of Bernoulli numbers:

\begin{align*} \frac{ x \pi }{ \sin( x \pi) } = \sum_{n=0}^\infty \dfrac{ 2 (2^{2n-1} - 1) (-1)^{n+1} \pi^{2n} B_{2n} }{ (2n)! } x^{2n} . \end{align*}

Employing this we obtain

\begin{align*} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x + 1)^2} dx & = \left. \dfrac{\partial^{2k}}{\partial \alpha^{2k}} \frac{\alpha \pi}{\sin( \alpha \pi)} \right|_{\alpha=0} \nonumber \\ & = 2 (2^{2k-1} - 1) (-1)^{k+1} \pi^{2k} B_{2k} . \end{align*}

We have $B_2 = \frac{1}{6}$. So that when $k=1$ we have

\begin{align*} \int_{-\infty}^\infty \dfrac{x^2 e^x}{(e^x + 1)^2} dx & = \frac{\pi^2}{3} . \end{align*}