Expected timing of an activation process

Question

Suppose we have $n$ sites and, within those sites, $m$ equally spaced positions, so that $2$ of those $m$ positions are in the extremities of the $n$ points. For $n=10$, for example, there are only the possibilities, $m=2$, $m=4$ and $m=10$, as sketched:

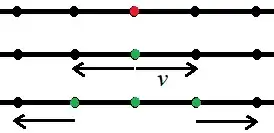
Now, assume each site in red activates at a rate $f$, after which it triggers an activation wave that propagates in both direction at a speed $v$, activating neighboring sites, as shown

Once a site is activated, it remains so. Note that dormant (unactivated) red sites can become activated from neighbouring activating waves.

My question is: how can I calculate the expected time it takes for a site (red or black) to be activated? In other words: how long, on average, does one site stay unactivated.

I understand if this problem becomes easier if we consider $n=m$ and/or a ring (periodic case), but I would just like to know where to start and how to think about a problem like this.

My attempt: It seems that, as a starting point, might be easier to consider the ring with $m=n$

To calculate the expected time it takes for a site to be activated, we can use a first-passage time analysis. This involves determining the probability that a site remains unactivated up to a certain time, and then taking the inverse of that probability.

Let's denote the probability that a site remains unactivated at time $t$ as $P(t)$. The rate at which a site becomes activated is equal to the rate of activation $f$ plus the rate at which an activation wave reaches it, which is equal to the product of the rate at which the neighboring site is activated ($f$) and the probability that the activation wave reaches the site before it has already been activated $(1-P(t-v/n))$. Therefore, we can write the following differential equation for $P(t)$ $$ \frac{dP(t)}{dt}=-f(1-P(t-v/n))-f $$ To solve this equation, we can use the initial condition $P(0) = 1$ (since all sites start unactivated) and the boundary condition $P(t) = 0$ for $t\geq T$ (where T is the maximum time we are interested in).

Once we have solved for $P(t)$, we can find the expected time for a site to be activated by taking the inverse of the probability that the site remains unactivated at time t. This can be found by the formula $E[T] = -1/P'(0)$.

This seems relatively correct, although I am not too sure whether the differential equation is quite correct, as the rate of wave activation should include other potential sites (rather than just immediate neighbours). Perhaps consider a sum of the form $2\sum_j^{\lfloor{n/2}\rfloor}P(t-v|i-j|/n)$, for a focal site $i$? Somewhat I feel the answer should be simpler, but I might be wrong. Any ideas?

Answer 1

I posted this already on a question about a smaller problem, but I am posting it here because it did resolve the general question.

First let me write out the nondimensionalization in this method. Let $T$ be the time to activation of our node of interest, let $t$ denote time as a variable, then introduce $\tilde{T}=fT$ and $\tilde{t}=ft$. Next introduce $\tilde{v}=v/f$, $s=1/\tilde{v}$. Throughout I will abuse notation by dropping tildes in the analysis.

The idea is to think of $T$ as an explicit function of the times the nodes would take to activate themselves if they were isolated. Let's call the self-activation time for node $i$ $A_i$. For ease of notation, I will index the nodes so that their distance from the node of interest is $|i|$ (thus there are nodes with negative index and nodes with positive index). In the ring network with all the nodes able to be activated, you have

$$T=\min_i \{ A_i + |i| s \}$$

since it takes time $|i| s$ for a wave from node $i$ to reach our node of interest. Note that in the ring network, the fact that the wave activates other nodes along the way does not matter.

This minimum is greater than some $t$ if all its components are, which occurs with probability

$$P(T>t)=\prod_i P(A_i>t-|i| s)=\prod_i \min \{ 1,\exp(-(t-|i| s)) \}.$$

So the expectation of the activation time for any one node is given as $E[T]=\int_0^\infty P(T>t) dt=\int_0^\infty \prod_i \min \{ 1,\exp(-(t-|i| s)) \} dt$. This integral can be split up at $s,2s,\dots,\lceil (n-1)/2 \rceil s$ for $n$ nodes, thus all the integrals can be done analytically.

The situation is slightly different between $n$ odd and $n$ even. When $n$ is odd, for each $k$, there are $2$ nodes at a distance of $k=1,2,\dots,(n-1)/2$ from the node of interest, for a total of $2k+1$ nodes at a distance of at most $k$. Additionally, we need to add up the distances up to $k$, each twice, which add up to $k(k+1)$. So we get

$$E[T]=\int_0^s e^{-t} dt + \sum_{k=1}^{(n-3)/2} \int_{ks}^{(k+1)s} e^{-(2k+1)t + k(k+1)s} dt + \int_{(n-1) s/2}^\infty e^{-nt+(n-1)(n+1) s /4} dt.$$

Doing the integrals yields:

$$E[T]=1-e^{-s} + \sum_{k=1}^{(n-3)/2} \frac{e^{-k^2 s}-e^{-(k+1)^2 s}}{2k+1} + \frac{e^{-(n-1)^2 s/4}}{n}.$$

Note that this formula works when $n=3$ with the sum understood as empty and thus zero. However, I don't see how to make it work when $n=1$.

When $n$ is even, for each $k$ there are $2$ nodes at a distance of $k=1,2,\dots,(n-2)/2$, and then there is $1$ node at a distance of $n/2$. Again we add up the distances, each twice, which add up to $k(k+1)$, but since there is only one node at a distance of $n/2$, the very last distance sum is $2+4+\dots+n-2+n/2=n(n-2)/4+n/2=n^2/4$. So we get

$$E[T]=\int_0^s e^{-t} dt + \sum_{k=1}^{(n-2)/2} \int_{ks}^{(k+1)s} e^{-(2k+1)t + k(k+1)s} dt + \int_{ns/2}^\infty e^{-nt+n^2s/4} dt.$$

Doing the integrals yields

$$E[T]=1-e^{-s} + \sum_{k=1}^{(n-2)/2} \frac{e^{-k^2 s}-e^{-(k+1)^2 s}}{2k+1} + \frac{e^{-n^2 s/4}}{n}.$$

Again this formula works when $n=2$ with the sum understood as empty and thus zero.

Reverting the change of variables, a general expression for any $n$ can be written as $$ E[T]=\frac1f\left[\sum_{k=0}^{\lceil(n-3)/2\rceil} \frac{e^{-fk^2 /v}-e^{-f(k+1)^2 /v}}{2k+1} + \frac{e^{-f(\lceil(n-1)/2\rceil)^2 /v}}{n}\right] $$ In particular, $E[T]=\frac1f$ for $n=1$.