What is the Expected Time of Crystallization?

Question

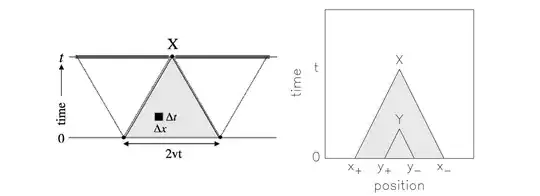
Consider the process of periodic 1D crystallization, where multiple sites initiate crystallizing waves at random with speed $v$. The fraction of the crystallized substance, at position $x$ and time $t$, is given by $$ f(x,t)=1-e^{-\int_{V_X(v)}p(Y) \,dY} $$ where $p(x,t)$ is the crystallization initiation rate at position $x$ and time $t$, and $V_X(v)$ is the past light-cone of the spacetime point $X=(x,t)$ (see figure below, where $x_\pm = x\mp vt$). My goal is to find an expression for $p$ in terms of the expected time of crystallization at each space point, which can be given by $$ t_E(x)=\int_0^\infty t \frac{\partial f(x,t')}{\partial t'}|_{t'=t} \,dt $$

Some ideas: From this paper (in the context of DNA replication, analogous to the process of 1D crystallization, see also this publication and chapter II of this thesis), defining the fraction of uncrystallized substance $s(x,t)=1-f(x,t)$, $p$ is shown to satisfy $$ p(x,t)=-\frac{v}{2}\square \log(s(x,t)), $$ where $\square =\frac{1}{v^2}\partial_t^2-\partial_x^2$ is the d'Alembert operator. Could I use this to write it in terms of the expected time of crystallization at each space point? I was thinking that, given the shape of $f$, perhaps a Laplace Transform could be used to rewrite the fraction $s$ in terms of the expected time at each space point, which would be our data.

A simple example: When $p(x,t)=p$ is constant in spacetime, we have $f(x,t)=1-e^{-pvt^2} $ and thus $$ t_E(x)=2pv\int_0^\infty t^2 e^{-pv t^2}\,dt=\frac12\sqrt{\frac{\pi}{pv}} $$ which can easily be inverted. Any ideas for the general case?

I was about to link to a past question of yours that I answered, since it seemed similar, and then I realized that it was in fact your question. +1, I will take another look at this later. — Ian, Oct 30 '23 at 14:52
@Ian Good to see you again. Thank you! If you do check the linked paper, check also this approach, where the math is slightly more detailed. I am ultimately interested in translating timing data to initiation rate, inverting the problem in an analytically accurate matter. — sam wolfe, Oct 30 '23 at 15:17
Looks like the first thing to be done is to deal with $\frac{\partial}{\partial t} \int_{V_X} p(Y) dY$, since that appears inside of the integral for $t_E(x)$. I guess the meaning of this derivative being partial is that $X$ (the start point of the light cone) changes only in time but the lightcone still changes (thus there is a "change of domain" contribution as well as an integral of $\frac{\partial}{\partial t} p(Y)$ contribution). — Ian, Oct 30 '23 at 16:17
After that it's just a highly nonlinear integral equation, which in general will be hard to solve analytically except for very special cases of $t_E(x)$. But it should be fairly tractable to solve numerically. I am somewhat skeptical that any general analytical solution can be developed if $t_E(x)$ can be whatever, especially if $v$ can be whatever. — Ian, Oct 30 '23 at 16:38
Understood, but is it possible to rewrite $p$ in terms of $t_E$ via the d'Alembert operator? Essentially, can I invert the expression for $t_E$ to write it in terms of $f$ (and consequently $s$)? — sam wolfe, Oct 30 '23 at 16:50
I'd actually venture a guess that in general $t_E(x)$ is not even enough information to specify $p$; consider that $p$ determines not just the first moment of the crystallization time at a particular point but the entire distribution of it. — Ian, Nov 01 '23 at 01:11
I see, but the timing data should uniquely define the probabilistic landscape, captured by $p$, no? — sam wolfe, Nov 01 '23 at 19:55
Timing data is given as the average replication time at each site — sam wolfe, Nov 02 '23 at 02:03
@Ian is right. Take e.g. $p=\alpha t$ then you can compute $t_E$ and fix $\alpha$ such that it matches the simple example you gave. With only $t_E$ you cannot discriminate between the two. — Ben, Nov 07 '23 at 22:28
If you mean “measuring” the Laplace transform as extra data then yes. — Ben, Nov 08 '23 at 12:06
Just to settle the question as best I can, since the bounty is lapsing: if all you know is $t_E$ then you have to assume something structural about $p$, basically pinning it down up to one free parameter for each fixed $x$. To determine it non-parametrically, you would need actual timing data rather than just expected values, thus your $f$ would be a Bernoulli random process rather than a continuous function. You could in principle describe this process using its MGF, but one way or the other you have to specify the whole thing or else assume something about the physics. — Ian, Nov 13 '23 at 15:21
@Ian Indeed. The expected time of initiation at $x$ (which is not the same as the expected crystallization time, $t_E$) should follow an exponential distribution with parameter $f(x)$. What is not clear to me, beyond the inversion problem, is how $f(x)$ and $p(x,t)$ are related. More relevant perhaps, is this follow-up question, which delves a bit more into the mathematical details that might not be so well explained in this question, I admit. It would be great if you could take a look at this one! Thanks — sam wolfe, Nov 13 '23 at 16:19
If the initiation time is exponentially distributed, then $p$ is not explicitly dependent on time (this is the "infinitesimal memoryless property" essentially), and now you have a well-defined integral equation. — Ian, Nov 13 '23 at 17:04
@Ian That makes sense, but how is $p$ related to $f$? If they are both constant (in space too), the expected time using $P(x,t)$ in the other question gives the same answer, but I am just confused about the terms being used in most of the linked papers for $I(x,t)$ ($p(x,t)$). Specifically, the thesis reads "We can then define the local initiation rate $I(x,t)$ as the probability the locus x, if not replicated at time t, to fire at t". This seems like a careless definition. Some other papers call it an initiation rate. How would you interpret this and relate it to the initiation rate, $f(x)$? — sam wolfe, Nov 13 '23 at 17:09
For constant $v$, $P(x \text{ is crystallized at time } t)=1-P(\forall s \in [0,t] , \forall y \in [x-vs,x+vs] , y \text{ does not self-activate by time } s)$. Do we agree up to that point? After that I believe you have $P(\forall s \in [0,t] , \forall y \in [x-vs,x+vs] , y \text{ does not self-activate by time } s)=\int_0^t \int_{x-vs}^{x+vs} \int_s^\infty f(y) e^{-f(y) u} du dy ds$. The inner integral is just $e^{-f(y) s}$, and now if this probability as a function of $x$ is given then you have a nonlinear integral equation for $f$. — Ian, Nov 13 '23 at 17:39
But I think I have made a mistake because this doesn't seem dimensionally consistent: somehow $f$ times $T$ is dimensionless but so is $f$ times $LT^2$. — Ian, Nov 13 '23 at 18:44
@Ian I guess your $f$ in this case is indeed $I(x,t)$, right? So you have derived the formula for the fraction of crystallized substance, $1-s(x,t)$ via light-cone (as in the linked question). You can also imagine a stochastic process where sites initiate at position-dependent rates (which determine the exponentially distributed initiation times). It might be the case the terms used in some of the linked papers are poor, hence why I am struggling to link $I(x,t)$ with my model: a process algebra to model stochastic dynamics using fixed rates at specific positions. Is this more or less clear? — sam wolfe, Nov 13 '23 at 18:46
If you remember this question these rates $f$ were positional-dependent (not in that question, but a general case is here). Yet these papers claim to have a general inverted formula. But they rely on $I(x,t)$, rather than a firing rate $f(x)$. All I am wondering is whether it is possible to build a bridge and actually use an analytical fit (in the case of non-uniform firing rates). — sam wolfe, Nov 13 '23 at 18:48
I see now it can be $I(x,t)$, now that I have the units straight. The key there is that there is not an activation rate, but an activation rate density, meaning the instantaneous rate of self-activation in a space interval $[a,b]$ at time $t$ is $\int_a^b I(x,t) dx$. In any case you need $P(x,t)$ (the probability that site $x$ is crystallized at time $t$) or something equivalent to it in order to solve this integral equation. — Ian, Nov 14 '23 at 14:38
@Ian So how do you relate the activation $f(x)$ rate to $I(x,t)$? — sam wolfe, Nov 17 '23 at 12:07
Same thing, but again it's not a rate, it's a rate density. I was confused earlier in thinking you could have bona fide rates at each site when you have a continuum of sites. — Ian, Nov 17 '23 at 12:28
@Ian Thank you. However. I am still struggling a bit with understanding their units. To me, $f(x)$ is a rate such that the time to activate follows an exponential with rate $f(x)$, at each site $x$. This is well-defined and is time-independent, how can $I(x,t)$ be the same? Could you please provide a detailed answer? Happy to award you the bounty for the linked question (this has expired), even though I do still require the inversion. This link between $I$ and $f$ is important, and I'm not yet fully certain I understand the difference. — sam wolfe, Nov 18 '23 at 11:33
A pure rate is not sensible here, because there are "too many sites". Even with countably many potential self-activation sites, you would need summability of all the $f(x)$ values. With continuum-many self-activation sites, effecticely everything crystallizes instantly. The way they are "the same" is that you can have a rate density that doesn't depend on time. — Ian, Nov 18 '23 at 12:56
I am afraid I might need a formalization of all this. I understand the original definition of $I(x,t)$ in the paper might be ambiguous, but I need to understand it in detail. In the original question (which you answered), I had indeed discrete values of $x$, but how does that actually relate to $I(x,t)$ in the continuous case? And, in particular, how does the time dependence come into play? — sam wolfe, Nov 18 '23 at 16:06

Ian · Answer 1 · 2023-11-27T16:57:37.763

This is just the derivation of the top equation, essentially.

Say the nucleation rate density (with dimension $L^{-1} T^{-1}$) is $I(x,t)$. Therefore the rate of a nucleation in $[a,b]$ at time $t$ is $R(a,b,t)=\int_a^b I(y,t) dy$. This has dimension $T^{-1}$.

Now let us consider an easier problem: the probability $Q(a,b,t)$ that a nucleation occurred in a fixed interval $[a,b]$ within time $t$ satisfies $\frac{\partial Q}{\partial t}(a,b,t)=R(a,b,t) (1-Q(a,b,t))$. The derivation of that is simple enough:

$$P(\text{nucleation within time } t+h) \\ =P(\text{nucleation within time } t)+P(\text{nucleation within time } t+h \mid \text{no nucleation within time } t) \\ \cdot P(\text{no nucleation within time } t) \\ Q(a,b,t+h)=Q(a,b,t)+hR(a,b,t)(1-Q(a,b,t))+o(h).$$

Hence

\begin{align}-\ln(1-Q(a,b,t)) & =\int_0^t R(a,b,s) ds \\ Q(a,b,t) & =1-e^{-\int_0^t R(a,b,s) ds} \\ & =1-e^{-\int_0^t \int_a^b I(y,s) dy ds}. \end{align}

To make the adjustment to this more complicated setting, you have to recompute that conditional probability, but everything else is the same. A close enough nucleation within time $t+h$ given that there were no close enough nucleations within time $t$ means that the nucleation occurred at a site $y \in [x-vt-vh,x+vt+vh]$ at a time $s$ such that $s \in [\max \{ 0,t-|y-x|/v \},t+h-|y-x|/v]$. The resulting figure in the spacetime diagram is a pair of trapezoids. If we neglect the two spacetime triangles on the far left and right which have area $O(h^2)$, then the entire region of interest has time width $h$, so the analogue of $hR(a,b,t)$ is $h \int_{x-vt}^{x+vt} I(y,t-|y-x|/v) dy$.

So the analogous equation for this setting is

$$P(x,t)=1-e^{-\int_0^t \int_{x-vs}^{x+vs} I(y,s-|y-x|/v) \, dy ds}$$

and the initial data is $P(x,0) \equiv 0$. You can strip out most of the nonlinearity by replacing the given quantity $P$ with $S:=-\ln(1-P)$, in which case you have

$$S=\int_0^t \int_{x-vs}^{x+vs} I(y,s-|y-x|/v) dy ds$$

and again $S(x,0) \equiv 0$.

From there I suppose you can derive that wave equation for $S$ with $I$ as forcing, which just solves the inverse problem completely, provided you have $S$. But with less information than that, you need to artificially create some additional information through something like an ansatz, otherwise you're stuck.

Within this formalism, if you have bare rates at a discrete set of sites $Y$ and no rate density otherwise, that amounts to having $I(x,t)=\sum_{y \in Y} \delta(x-y) f(y,t)$.

This is much more clear now! Given this formulation, what would be $f(x)$, defined as the rate of nucleation at position $x$? Would that be given by $f(x)=\int_0^\infty I(x,t),dt$? Perhaps it does not make sense to talk about this rate, but from the different framework, where $f(x)$ determined the exponentially distributed nucleation times at specific sites $x$, it still is not clear how $f$ relates to $I$. — sam wolfe, Nov 21 '23 at 17:02
Is it simply the case that $f(x)=I(x,t)$ is a particular case when $I$ is time-independent? From its definition, I wouldn't expect that (I think?). What is particularly strange is that, when $f(x)=I(x,t)=f$ is constant, the expected nucleation time calculated here matches the approximation from the different approach, as shown here. I am really only missing the linking point in these definitions. — sam wolfe, Nov 21 '23 at 17:13
@samwolfe The nucleation rate (a bare rate, not a rate density) is necessarily zero at all but countably many sites, otherwise the nucleation events can't occur at discrete times. Of course you can instead do something like setting up a finite nucleation rate at just some sites; this amounts to having $\delta(x)$ terms in $I(x,t)$. If the nucleation rate density is just a sum of delta functions in space with time-and-space-independent coefficients then indeed you recover the other problem. — Ian, Nov 21 '23 at 17:20
that makes sense, I was just about to add that the missing link could be the discretization implied in the original problem. I suspect that inverting the problem is considerably harder in the discrete case, so perhaps the other approach is better in that sense? — sam wolfe, Nov 21 '23 at 17:34
Would you be able to include that discretization and explicit relation between $f$ and $I$ in your answer? I believe what you mean is something along the lines of what is shown in equation (5) of the methods in this paper (page 10), correct? I ultimately want to map timing to the firing rate $f(x)$, if possible? — sam wolfe, Nov 22 '23 at 01:09

What is the Expected Time of Crystallization?

1 Answers1