I'm not sure on how to find the gradient in polar coordinates. The thing that troubles me the most is how to find the unit vectors $\hat{r}$ and $\hat{\theta}$. My approach for the rest is expressing the partial derivatives in respect of $r$ and $\theta$ using the chain rule.
How can I get around solving this problem?
The gradient operator in 2-dimensional Cartesian coordinates is $$ \nabla=\hat{\pmb e}_{x}\frac{\partial}{\partial x}+\hat{\pmb e}_{y}\frac{\partial}{\partial y} $$ The most obvious way of converting this into polar coordinates would be to write the basis vectors $\hat{\pmb e}_x$ and $\hat{\pmb e}_{y}$ in terms of $\hat{\pmb e}_{r}$ and $\hat{\pmb e}_{\theta}$ and write the partial derivatives $\frac{\partial}{\partial x}$ and $\frac{\partial}{\partial y}$ in terms of $\frac{\partial}{\partial r}$ and $\frac{\partial}{\partial \theta}$ using the chain rule.
So we have: $$ \begin{align} \hat{\pmb e}_{x}&=\cos\theta\, \hat{\pmb e}_{r}-\sin\theta\, \hat{\pmb e}_{\theta} \\ \hat{\pmb e}_{y}&=\sin\theta\, \hat{\pmb e}_{r}+\cos\theta\, \hat{\pmb e}_{\theta} \\ &\\ \frac{\partial}{\partial x}&=\frac{\partial r}{\partial x}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta} \\ \frac{\partial}{\partial y} &=\frac{\partial r}{\partial y}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial y}\frac{\partial}{\partial \theta} \end{align} $$ Observing that $r=\sqrt{x^2+y^2}$ and $\theta=\arctan\left(\frac{y}{x}\right)$, we have $$ \begin{align} \frac{\partial r}{\partial x}&=\cos\theta &\frac{\partial r}{\partial y}&=\sin\theta\\ \frac{\partial\theta}{\partial x}&=-\frac{\sin\theta}{r} & \frac{\partial\theta}{\partial y}&=\frac{\cos\theta}{r} \end{align} $$ and $$ \begin{align} \nabla&=\hat{\pmb e}_{x}\frac{\partial}{\partial x}+\hat{\pmb e}_{y}\frac{\partial}{\partial y}\\ &=(\cos\theta\, \hat{\pmb e}_{r}-\sin\theta\, \hat{\pmb e}_{\theta})\left(\frac{\partial r}{\partial x}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta}\right)+(\sin\theta\, \hat{\pmb e}_{r}+\cos\theta\, \hat{\pmb e}_{\theta})\left( \frac{\partial r}{\partial y}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial y}\frac{\partial}{\partial \theta} \right)\\ &=\ldots\\ &=\hat{\pmb e}_{r}\frac{\partial }{\partial r}+\hat{\pmb e}_{\theta}\frac{1}{r}\frac{\partial }{\partial \theta}. \end{align} $$
This certainly gives the right answer, but there is a quicker way. Consider a function $f(\pmb r)$ in polar coordinates: this is a function $f(r,\theta)$. The small change in going from the point $\pmb r$ with coordinates $(r,\theta)$ to the point $\pmb r+\operatorname{d}\pmb r$ with coordinates $(r + \operatorname{d}r,\theta + \operatorname{d}\theta)$ is $$ \operatorname{d}f=\frac{\partial f}{\partial r}\operatorname{d}r+\frac{\partial f}{\partial \theta}\operatorname{d}\theta \tag 1 $$ Observe that $\operatorname{d}f=\operatorname{d}\pmb r\cdot \nabla f$ and $\operatorname{d}\pmb r=\operatorname{d}r\hat{\pmb e}_{r}+r\operatorname{d}\theta \hat{\pmb e}_{\theta}$. Suppose, then, that $$ \nabla f=\alpha\hat{\pmb e}_{r}+\beta \hat{\pmb e}_{\theta} $$ where $\alpha$ and $\beta$ are to be found. We get $$\operatorname{d}f=\operatorname{d}\pmb r\cdot \nabla f=\left(\operatorname{d}r\hat{\pmb e}_{r}+r\operatorname{d}\theta \hat{\pmb e}_{\theta}\right)\cdot\left(\alpha\hat{\pmb e}_{r}+\beta \hat{\pmb e}_{\theta}\right)=\alpha\operatorname{d}r+\beta r\operatorname{d}\theta \tag 2$$ because $\hat{\pmb e}_{r}\cdot\hat{\pmb e}_{r}=\hat{\pmb e}_{\theta}\cdot \hat{\pmb e}_{\theta}=1$ and $\hat{\pmb e}_{\theta}\cdot \hat{\pmb e}_{r}=0$. Comparing (1) and (2) we see that $\alpha=\frac{\partial f}{\partial r}$ and $\beta=\frac{1}{r}\frac{\partial f}{\partial \theta}$. Therefore, we get $$\nabla f=\hat{\pmb e}_{r}\frac{\partial f}{\partial r}+\hat{\pmb e}_{\theta}\frac{1}{r}\frac{\partial f}{\partial \theta}$$ and we can identify the gradient operator itself as $$ \nabla =\hat{\pmb e}_{r}\frac{\partial }{\partial r}+\hat{\pmb e}_{\theta}\frac{1}{r}\frac{\partial }{\partial \theta}. $$
This version is for those, who prefer a different notation. $$ u \circ \sigma = f, \text { where } \sigma(x,y) = \left(\sqrt{x^2+y^2}, \arctan\frac yx\right)$$ Fix $a=(x,y) = r(\cos\theta,\sin\theta)$. Let $(Df)(a)$ and $(\nabla f)(a)$ denote the linear operator and the vector representing it. By the chain rule, $$(Df)(a) = (Du)(\sigma(a)) \circ (D\sigma)(a).$$ Implying that \begin{align} (\nabla f)(a) &= (\nabla u)(\sigma(a))\cdot \pmatrix{ \cos\theta & \sin\theta \\ -\frac 1 r\sin\theta & \frac 1r\cos\theta} \\ &= u_r(\sigma(a))\cdot(\cos\theta , \sin\theta) + \frac 1r u_{\theta}(\sigma(a))\cdot(-\sin\theta, \cos \theta). \end{align} Let's hold on for a minute and observe our result: The vector $(\nabla f)(a)$ is a linear combination of the vectors $(\cos\theta,\sin\theta)$, and $(-\sin\theta, \cos\theta)$.
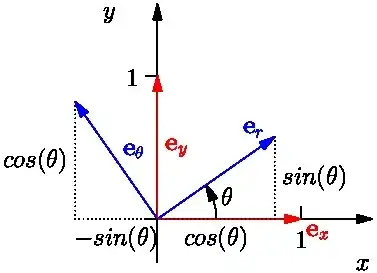
In fact, \begin{align}\{\, \boldsymbol{e_r} &= (\cos\theta,\sin\theta)\\ , \boldsymbol{e_{\theta}} &= (-\sin\theta, \cos\theta)\}\end{align} is a basis for $\mathbb R^2$. Using our new notation, the equation above becomes
$$ (\nabla f)(a) = u_r(\sigma(a))\cdot \boldsymbol{e_r} + \frac 1r u_{\theta}(\sigma(a))\cdot \boldsymbol{e_{\theta}} = \left(u_r(\sigma(a)), \frac 1r u_{\theta}(\sigma(a))\right) = (\nabla(u))(\sigma(a))\cdot\pmatrix{1 \\ \frac 1r},$$
or equivalently, $$ (\nabla f)(r(\sin\theta, \cos\theta)) = \left(u_r(r, \theta), \frac 1r u_{\theta}(r, \theta)\right) = (\nabla u)(r,\theta)\cdot\pmatrix{1 \\ \frac 1r}. $$
If we start omitting a few variables, things become prettier, but also somewhat easier to misunderstand.
$$ \nabla f = \nabla u \cdot \pmatrix{1 \\ \frac 1r} = \left(u_r, \frac 1r u_{\theta}\right) = \boldsymbol{e_r} u_r + \boldsymbol{e_{\theta}} \frac 1r u_{\theta} =\boldsymbol{e_r} \frac{\partial u}{\partial r}+ \boldsymbol{e_{\theta}}\frac 1r \frac{\partial u}{\partial \theta} $$ We can also omit function names, leading to
$$ \nabla = \boldsymbol{e_r} \frac{\partial}{\partial r}+ \boldsymbol{e_{\theta}} \frac 1r \frac{\partial}{\partial \theta}. $$