For the flow $A = \frac{c}{r}$ with $r=\sqrt{x^2+y^2+z^2}$ I wanted to calculate the velocity field with $\nabla A$
As a result I get $(-\frac{c}{r^2},0,0)$. So far so good. When I tried converting it to cartesian coordinates I'm stuck.
I would have inserted the given $r$ in my solution however wolfram alpha & the solution suggest the solution in cartesian coordinates is:
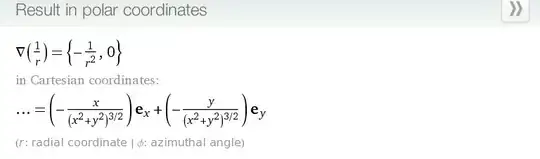
Converting with $x=\sqrt{x^2+y^2+z^2} \cos(0)$ does not really work. I'm sure I'm currently having a major blackout in seeing something elemental missing here.