18

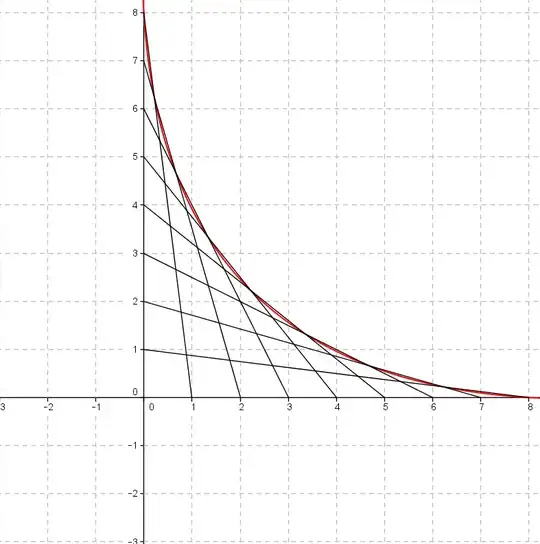
When I was a kid I used to draw this shape below but today I came against it as a problem. I don't know the name of this red curve below. It is enough to say the name if it is a known curve. I will search for it's properties. enter image description here

The shape is constructed with lines from point $(0,n)$ to $(8-(n-1),0)$ and the curves passes through the intersection of each two lines. In contrast to the figure, the red curve never crosses the axes. $n=0,1,...,9$ however the shape does not need to be discrete, hence $n$ can go to $0$. Probably the values on the axes are not important to know the name of the curve.

newzad
  • 4,923

7 Answers7

16

The particular curve suggested, tangent to all of the segments from $(0,a)$ to $(9-a,0)$ as $a$ runs from $0$ to $9$, is this one: $$ y = x-6\sqrt{x}+9 $$

This is a portion of a parabola, with axis on the $x=y$ line and vertex at $(9/4,9/4)$.

To see this more clearly, add also such lines with $a>9$ and $a<0$ ...

enter image description here

GEdgar
  • 117,296
11

For this particular example, the red curve is "stitched" by a family of straight lines of $$\begin{align*} \frac x{9-k} + \frac yk =& 1\\ y =& k - \frac{kx}{9-k} \end{align*}$$ where $0<k<9$.

When there are two such straight lines with parameters $h$ and $k$ respectively, $h\ne k$, $$\begin{align*} y =& h - \frac{hx}{9-h}\\ y =& k - \frac{kx}{9-k}\\ \end{align*}$$

Their intersection can be calculated as $$\begin{align*} h - \frac{hx}{9-h} =& k - \frac{kx}{9-k}\\ \frac{kx}{9-k} - \frac{hx}{9-h} =& k - h\\ x\cdot\frac{9k-hk-9h+kh}{(9-k)(9-h)} =& k - h\\ x =& \frac{(9-k)(9-h)}9\\ \end{align*}$$

When we take $h\to k$, the $x$-coordinates becomes $$x = \frac{(9-k)^2}9$$

and the $y$-coordinates is $$y = k - \frac{kx}{9-k} = k - \frac{k(9-k)}{9} = \frac{k^2}9$$

We can get an implicit curve for our range $$\sqrt x + \sqrt y = 3$$

peterwhy
  • 22,930
5

It's a quadratic Bézier curve.

shade4159
  • 807
  • 3
    It's a quadratic Bezier segment, with control points (0, 9), (0, 0), and (9, 0), I believe. That means that you can write it as $t^2 (9, 0) + 2t(t-1) (0, 0) + (1-t)^2 *(0, 9)$, which simplifies to $(9 t^2, 9(1-t)^2)$. Just in case you have access to matlab, here's code to make the picture:

    t = linspace(0, 1, 200); x = 9 * t.^2; y = 9 * (1-t).^2;

    plot(x, y); hold on; % draw the lines for i = 0:9 plot( [0, 9-i], [i, 0], 'r'); end set(gca, 'DataAspectRatio', [1 1 1]); hold off; figure(gcf);

     – John Hughes Nov 04 '13 at 18:58
  • @John thank you very much, your comment is very useful. – newzad Nov 04 '13 at 19:04
  • This is a good (best?) answer because it directly addresses the construction of the curve from line segments. This process is De Casteljau's algorithm. – PtH Jul 05 '19 at 02:46
5

It's a (portion of a) parabola.

By the curve-stitching construction, it's what's called an "envelope" of the family of line segments. The Wikipedia article (starting at "For example, let $C_t$ be the lines whose $x$ and $y$ intercepts are $t$ and $1-t$...") walks somewhat quickly through your problem as its example (except with $x$ and $y$ intercepts of $1$ instead of $9$).

Blue
  • 83,939
1

This curve is a rotated parabola. As drawn in the picture, you get a parametric curve with: $$x = \frac{(t-7)(t-8)}{9}, y = \frac{(t+1)(t+2)}{9}$$ Applying a $45$° rotation counterclockwise, you get:

$$\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} \sin(45) & -\cos(45) \\ \cos(45) & \sin(45) \end{array} \right) \times \left( \begin{array}{ccc} x \\ y \end{array} \right)$$

Plugging the parametrized forms of $x$ and $y$, you can see, by direct check, that:

$$ y' = \frac{\sqrt{2}(x')^2}{162}+20\sqrt{2}$$

rmdmc89
  • 10,709
  • 3
  • 35
  • 94
1

As I wrote elsewhere, we are most probably dealing with a superellipse, a geometric shape described by algebraic equations of the form $x^n+y^n=r^n$, perhaps with $n=\frac12$ or $\frac23$ (astroid) , or maybe some other form of hypocycloid. Their bidimensional generalizations are called superformulas, and their three-dimensional counterparts are known as superellipsoids, superquadrics or supereggs. The case $n=4$ is called a squircle. Hope this helps.

Community
  • 1
Lucian
  • 49,312
0

Though probably not equivalent, it is similar to a hyperbola in the first quadrant. Try graphing points for the equation $y = \dfrac{1}{x}$ to see a basic example. Changing the value in the numerator above $x$ is what dictates how far away the whole curve is from at the origin at its closest point (which is on the line $x=y$). Also, a numerator that is an integer with several divisors will also have several integer solutions for $(x,y)$.

Example: Graph the equation $y=\dfrac{20}{x}$ and see how it has integer solutions at (1,20), (2,10), (4,5), (5,4), (10,2), and (20,1).

Xoque55
  • 4,499
  • That was my first thought too. But the other answers convinced me that it's a parabola. – TonyK Nov 04 '13 at 19:38