Based on my last question I learned that this is an envelope of a parabola
What is this geometric pattern called?
But how can I prove it ?
Asked
Active
Viewed 456 times
2 Answers
2
We try to model the family of lines and then try to infer the envelope.
The guiding lines (left and right arms of the V shape) are $$ g(t) = u_g \, (1-t) + v_g \, t \quad h(t) = u_h \, (1-t) + v_h \, t $$ for $t \in [0, 1]$, where $u$ is the start point and $v$ the end point of that line.
A line $f_r$ of the family starts on $g$ and ends on $h$: $$ f_r(t) = g(r) \, (1-t) + h(r) \, t $$ again with the parameter $t \in [0, 1]$.
The envelope is approximated by points where two of the family lines intersect: $$ \begin{align} f_r(t) &= f_s(t') \iff \\ g(r) \, (1-t) + h(r) \, t &= g(s) \, (1-t') + h(s) \,t' \end{align} $$
This gives the matrix equation $$ \left[ \begin{matrix} h(r) - g(r) & -(h(s) - g(s)) \end{matrix} \right] \left[ \begin{matrix} t \\ t' \end{matrix} \right] = g(s) - g(r) \quad (*) $$
Example: $$ u_g = \left[ \begin{matrix} -1 \\ 1 \end{matrix} \right] \quad v_g = \left[ \begin{matrix} 0 \\ -1 \end{matrix} \right] \quad u_h = \left[ \begin{matrix} 0 \\ -1 \end{matrix} \right] \quad v_h = \left[ \begin{matrix} 1 \\ 1 \end{matrix} \right] $$
This gives $$ g(r) = \left[ \begin{matrix} r - 1 \\ 1 - 2r \end{matrix} \right] \quad h(r) = \left[ \begin{matrix} r \\ 2r - 1 \end{matrix} \right] \quad g(s) = \left[ \begin{matrix} s - 1 \\ 1 - 2s \end{matrix} \right] \quad h(s) = \left[ \begin{matrix} s \\ 2s - 1 \end{matrix} \right] $$ and thus for two different family lines ($r \ne s$): $$ \left[ \begin{matrix} 1 & -1 \\ 4r-2 & 2 - 4s \end{matrix} \right] \left[ \begin{matrix} t \\ t' \end{matrix} \right] = \left[ \begin{matrix} s - r \\ 2 (r - s) \end{matrix} \right] $$ The first row gives $t' = t + r - s$ and the second row $$ 2(r-s) = (4r-2)t + (2-4s)(t+r-s) = 4(r-s) t + (2-4s)(r-s) \iff \\ 4s(r-s) = 4(r-s) t \iff \\ t = s $$
and thus $t' = r$. The intersection point results to $$ p(r,s) = f_r(s) = f_s(r) $$ however we want $r \to s$ and thus: $$ p(r) = f_r(r) = \left[ \begin{matrix} (r-1)(1-r) + r^2 \\ (1-2r)(1-r) + (2r-1) r \end{matrix} \right] = \left[ \begin{matrix} 2r - 1 \\ 4r^2 -4r + 1 \end{matrix} \right] $$ Substituting $x = 2 r - 1 \iff r = (x + 1) / 2$ and remembering $r \in [0, 1]$ we get $$ p(x) = \left[ \begin{matrix} x \\ 4\left(\frac{x+1}{2}\right)^2 -4 \frac{x+1}{2} + 1 \end{matrix} \right] = \left[ \begin{matrix} x \\ x^2 \end{matrix} \right] $$ which is the graph of a parabola.
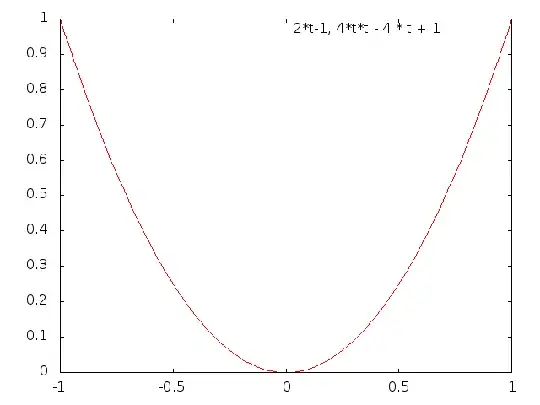
Note:
I picked the example to correspond to a nice symmetric V shape. Equation (*) holds for general situations, e.g. a V with a longer and a shorter arm. In those cases, other envelopes, if at all, arise!
E.g. it is possible to arrange the guiding lines as a | | shape, where the result should look like a butterfly or a (boring) stripes pattern, depending on the relative orientations of the guiding lines.
mvw
- 35,114
1
The curve you see is by definition a quadratic bézier curve which is always a segment of a parabola.