3

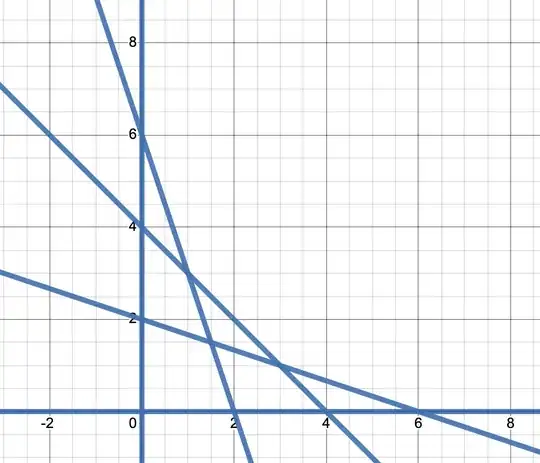
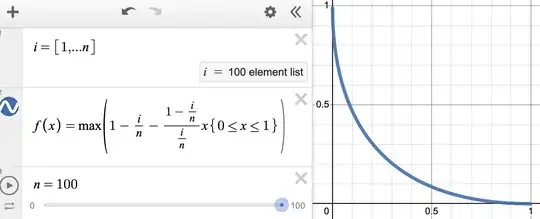
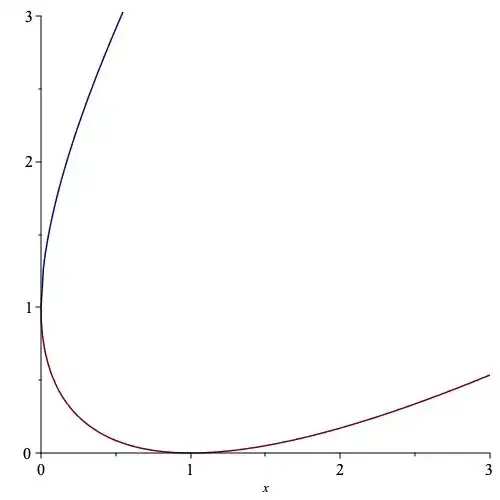
Hello Math StackExchange! When I was in grade school, our math class did an art project where we drew many straight lines to make what appears to be a curve on the outside (pictures attached). I've been curious about the resulting curve for at least a year, and upon dedicating time toward it, I still can't get a satisfactory solution (besides a brute force method with the max(x,y) function). Is there a closed form for the limiting case of this curve? Is a closed form impossible?

Case of 5 lines:

Case of 100 lines:

dxiv
  • 77,867
Jenny Pianist
  • 33
  • What is the rule for creating such lines ? – conan Jul 30 '23 at 21:38
  • @conan it looks like the rule is to choose some real number, $x$ and natural number $n$. The first line is the line connecting the points $(0,x/2)$ and $(x/2,0)$ then the next line connects $(0+x/n, x/2 -x/n)$ and $(x/2-x/n, 0+x/n)$, and keep rotating like this until one component in each coordinate reaches $0$ again, and then duplicate and reflect all the lines about the line $y=x$ – Carlyle Jul 30 '23 at 21:47
  • 1
    I think you might be talking about an envelope of a family of lines – Deif Jul 30 '23 at 21:50
  • 3
    Lookup the envelope of a family of curves. In your case $F(t,x,y) = y - 1 + t + \frac{1-t}{t} x$, and after doing the calculations you get the envelope $(x-y+1)^2 - 4 x = 0$ $\iff y = x + 1 - 2 \sqrt{x}$. – dxiv Jul 30 '23 at 21:56
  • 1
    Note that $\sqrt{x}+\sqrt{y}=1.$ It is a special case of $x^p+y^p=1.$ – Somos Jul 30 '23 at 22:47

3 Answers3

5

Seems like you're looking for a closed form for the function defined as $$y(x) = \max_{p\in [0,1]} \Big(1-p-\tfrac{1-p}{p}x\Big)$$ for $x\in [0,1]$. Notice that we can rewrite the expression in parentheses as follows: $$1-p-\tfrac{1-p}{p}x = 1+x - 2\sqrt{x} - \Big(\sqrt{p} - \sqrt{\tfrac{x}{p}}\Big)^2$$ Because perfect squares of real numbers are always nonnegative, we can argue that this expression is always at most $1+x-2\sqrt{x}$. Furthermore, this value is actually achieved when $p=\sqrt{x}$. Hence, we have that $$y(x) = 1+x-2\sqrt{x}$$ and voila: enter image description here

Franklin Pezzuti Dyer
  • 40,930
  • 9
  • 80
  • 174
0

To answer Vincent Batens' question, what I first did was consider a very discrete solution like in picture 1 with an arbitrary n lines (because of Mr. Sanderson as you all know). Every curve can be parametrized by the value i/p (i in mine, p in Dyer's) for any given x; that's tedious algebra that is really annoying to simplify but is clear enough. The max function can be explained verbally:

For every line that can be parametrized at this x value, one of them has the highest value (which is what defines the height of the curve), so pick that as the curve.

Jenny Pianist
  • 33
0

parabola

Note that our graph $y=x+1-2\sqrt{x}$ is part of a parabola.

parabola

GEdgar
  • 117,296