1

On the first quadrant, we connect with a segment all pairs of points $(x,0)$ to $(0,y)$ such that $x,y\in\mathbb{R}^+$ and $x+y=10$. Find the area of the region created by the segments.

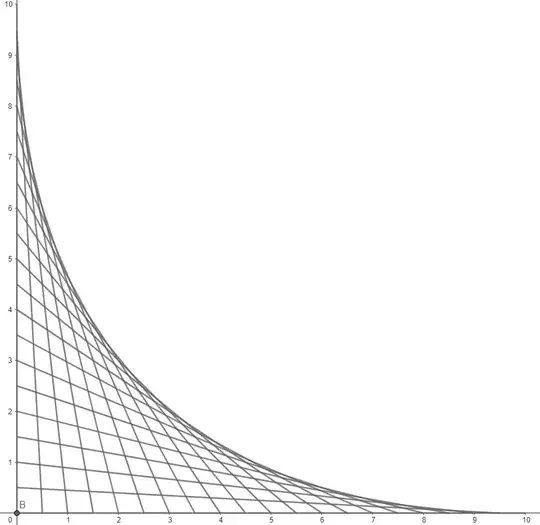
Here's a diagram with some of the segments: Some of the segments

It may look like the answer is a square minus a quarter circle, but its actually less than that: A circle

I also tried to move the circle's center and radius, but none of them is match the curve of the segments. Any idea on how I could solve this question?

Blue
  • 83,939
TNT1288
  • 87
  • @RobinSparrowdo you know the name of the problem? – TNT1288 Sep 06 '24 at 21:16
  • Also, the ladder/pole in the calculus problem would always have the same length. However, almost all the segments are different. – TNT1288 Sep 06 '24 at 21:19
  • 1
    See here: https://math.stackexchange.com/questions/4691104/the-area-between-parabolic-lines-inside-a-square – Intelligenti pauca Sep 06 '24 at 21:26
  • 1
    See also https://math.stackexchange.com/q/551882/442 (the curve is a parabola). – GEdgar Sep 07 '24 at 14:06
  • 2
    @TNT1288: Do not vandalize questions (including your own). Also, please don't delete them (even if declared duplicate) if someone has taken the time to provide an answer. – Blue Nov 29 '24 at 02:46

1 Answers1

3

The curve "created" by the segments is called the envelope of the lines, and is defined as the curve which is tangent to all the lines. I'll show that this curve is a parabola, with focus $C=(5,5)$ and directrix with equation $x+y=0$. I won't use calculus, but a geometric argument.

Consider then a line $AB$ with $A=(a,0)$ and $B=(0,10-a)$ and note that $CAB$ is a right isosceles triangle. Draw then a line $A'B'$ with $A'=(a',0)$ and $B'=(0,10-a')$, intersecting $AB$ at point $Q$. $CA'B'$ is also a right isosceles triangle, implying that $$ \angle QAC=\angle QA'C'=45°. $$ As a consequence, points $AA'CQ$ lie on the same circle.

enter image description here

I want to find the position $P$ of point $Q$ in the limit $A'\to A$, because such $P$ is a point on the envelope. As $A'\to A$, circle $A'AC$ approaches the circle through $C$ which is tangent to the $x$-axis at $A$ (blue in figure below). Point $P$ is then the intersection between that circle and line $AB$.

The construction of the center $G$ of this circle and then of point $P$ is straightforward, also because $\angle CGP=2\angle CAP=90°$. You can check that:

$$ G=\left(a,{(5-a)^2+25\over10}\right); \quad P=\left({a^2\over10},{(10-a)^2\over10}\right). $$

enter image description here

Finally, we can check that $PC=PH$, where $H$ is the projection of $P$ on the line $x+y=0$ (this check is left to the reader – note that $H$ is the reflection of $C$ about the midpoint of $AB$), thus proving that $P$ lies on the parabola with focus $C$ and directrix with equation $x+y=0$. The parabola touches the cartesian axes at $D=(10,0)$ and $E=(0,10)$, its axis is line $OC$ and its vertex is $V=(5/2,5/2)$.

The requested area can also be computed without calculus, using Archimedes' theorem, as the difference between triangle $ODE$ and the segment of parabola $VDE$: $$ area={1\over2}10\cdot10-{4\over3}\cdot{1\over2}\cdot 10\sqrt2\cdot{5\over2}\sqrt2={50\over3}. $$

Intelligenti pauca
  • 55,765