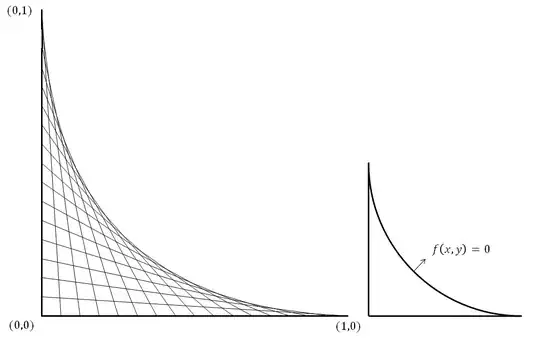
Hint: find the general equation for the lines.
Then, find a formula for "the point $(x,y)$ lies above and to the right of a given line".
To find the general equation for the lines, we can use the description that we've divided the axes into equal pieces. If there are $n$ equal pieces, then there are $n-1$ points in those intervals $[0,1]$, located at distances $m/n$ from the origin, where $m$ is a positive integer less than $n$.
The line attached to $(m/n, 0)$ has $(0, (n-m)/n) = (0, 1 - m/n)$ as its other end point. (There are lots of ways to see this: I'll let you choose your own!)
To save writing, I'll let $a = m/n$, so the line segments connect $(a,0)$ to $(0, 1-a)$.
Now, we can any method for obtaining the equation of a line through $(a,0)$ and $(0, 1-a)$. We could use the two-point form. We could use slope intercept form. I'll demonstrate a method that doesn't rely on actually remembering something: the equation of a line always looks like
$$ c x + d y = e $$
for some $c$, $d$, and $e$. Since those two points have to lie on it, we have a system of equations:
$$ ca + d0 = e \qquad \qquad c0 + d(1-a) = e $$
or more simply
$$ ac = e \qquad \qquad d(1-a) = e $$
and we just need any solution that is not all zeroes. One such solution is
$$ c = \frac{1}{a} \qquad \qquad d = \frac{1}{1-a} \qquad \qquad e = 1 $$
Aside: we could have taken a different starting point: e.g. we could have said the equation of a non-vertical line always looks like $y = cx + d$, and taken the same approach to figure out what $c$ and $d$ are.
So, the equations for the line all look like
$$ \frac{x}{a} + \frac{y}{1-a} = 1 $$
One side of the line is given by the inequality
$$ \frac{x}{a} + \frac{y}{1-a} > 1 $$
and the other by
$$ \frac{x}{a} + \frac{y}{1-a} < 1 $$
We want the inequality that describes points being above/to the right of the line. While you could try to "reason it out", an easier approach is just to observe that we want the side containing $(1,1)$. An even easier approach is to observe we don't want the side containing $(0,0)$. If we plug in $(0,0)$ into the left hand side, we get zero. So we don't want the second one.
Thus, every point on and above your beauty curve satisfies the inequality
$$ \frac{x}{a} + \frac{y}{1-a} \geq 1 $$
for every rational value of $a \in (0,1)$. It really ought to satisfy the inequality for every $a \in (0,1)$ too.
If your curve behaves as nicely as it looks, this inequality should be an actual equality for exactly one value of $a$.
So which points $(x,y)$ satisfy this inequality for all values of $a$? Well, let's solve for which $a$'s it does satisfy!
First combine the fractions:
$$ \frac{x(1-a) + ya}{a(1-a)} \geq 1 $$
Now multiply through by the denominator. Don't forget to check the sign! It's positive, so that means the inequality stays in the same direction. So, we get
$$ x(1-a) + ya \geq a(1-a) $$
collecting the $a$'s together:
$$ a^2 + a(y-x-1) + x \geq 0 $$
(and we also have $0 < a < 1$). This is a quadratic function of $a$: for each particular value of $x,y$, it's graph is a parabola.
Since we want the points actually on the beauty curve, we desire that the actual equation
$$ a^2 + a(y-x-1) + x = 0 $$
have exactly one solution for $a$. Recall that the solutions are, by the quadratic formula,
$$ a = \frac{(1+x-y) \pm \sqrt{(1+x-y)^2 - 4x}}{2} $$
If there is only one solution, then that square root must actually be zero. That is, we need
$$ (1+x-y)^2 - 4x = 0 $$
or equivalently
$$ x^2 - 2xy + y^2 - 2x - 2y + 1 = 0 $$
If you study conic sections a lot, you'll notice the quadratic terms are
$$ x^2 - 2xy + y^2 = (x-y)^2$$
which signifies that your curve is actually part of a parabola. Here is a plot using Wolfram alpha