Nice proofs of $\zeta(4) = \frac{\pi^4}{90}$?

Question

I know some nice ways to prove that $\zeta(2) = \sum_{n=1}^{\infty} \frac{1}{n^2} = \pi^2/6$. For example, see Robin Chapman's list or the answers to the question "Different methods to compute $\sum_{n=1}^{\infty} \frac{1}{n^2}$?"

Are there any nice ways to prove that $$\zeta(4) = \sum_{n=1}^{\infty} \frac{1}{n^4} = \frac{\pi^4}{90}?$$

I already know some proofs that give all values of $\zeta(n)$ for positive even integers $n$ (like #7 on Robin Chapman's list or Qiaochu Yuan's answer in the linked question). I'm not so much interested in those kinds of proofs as I am those that are specifically for $\zeta(4)$.

I would be particularly interested in a proof that isn't an adaption of one that $\zeta(2) = \pi^2/6$.

Answer 1

In the same spirit of the 1st proof of this answer. If we substitute $\pi $ for $ x $ in the Fourier trigonometric series expansion of $% f(x)=x^{4}$, with $-\pi \leq x\leq \pi $,

$$x^{4}=\frac{1}{5}\pi ^{4}+\sum_{n=1}^{\infty }\frac{8n^{2}\pi ^{2}-48}{n^{4}}\cos n\pi \cdot \cos nx,$$

we obtain

$$\begin{eqnarray*} \pi ^{4} &=&\frac{1}{5}\pi ^{4}+\sum_{n=1}^{\infty }\frac{8n^{2}\pi ^{2}-48}{n^{4}}\cos ^{2}n\pi \\ &=&\frac{1}{5}\pi ^{4}+8\pi ^{2}\sum_{n=1}^{\infty }\frac{1}{n^{2}} -48\sum_{n=1}^{\infty }\frac{1}{n^{4}}. \end{eqnarray*}$$

Hence

$$\sum_{n=1}^{\infty }\frac{1}{n^{4}}=\frac{\pi ^{4}}{48}\left( -1+\frac{1}{5}+ \frac{8}{6}\right) =\frac{\pi ^{4}}{48}\cdot \frac{8}{15}=\frac{1}{90}\pi ^{4}.$$

Answer 2

Consider the function $f(t):=t^2\ \ (-\pi\leq t\leq \pi)$, extended to all of ${\mathbb R}$ periodically with period $2\pi$. Developping $f$ into a Fourier series we get $$t^2 ={\pi^2\over3}+\sum_{k=1}^\infty {4(-1)^k\over k^2}\cos(kt)\qquad(-\pi\leq t\leq \pi).$$ If we put $t:=\pi$ here we easily find $\zeta(2)={\pi^2\over6}$. For $\zeta(4)$ we use Parseval's formula $$\|f\|^2=\sum_{k=-\infty}^\infty |c_k|^2\ .$$ Here $$\|f\|^2={1\over2\pi}\int_{-\pi}^\pi t^4\>dt={\pi^4\over5}$$ and the $c_k$ are the complex Fourier coefficients of $f$. Therefore $c_0={\pi^2\over3}$ and $|c_{\pm k}|^2={1\over4}a_k^2={4\over k^4}$ $\ (k\geq1)$. Putting it all together gives $\zeta(4)={\pi^4\over 90}$.

Answer 3

If you are specially interested only in $\zeta(4)$, the following proof would work but this is an adaptation Euler's idea. The idea is just to mimic Euler's proof for the Basel problem. Euler looks at the function whose zeros are at $\pm \pi, \pm 2 \pi, \pm 3 \pi, \ldots$

To evaluate $\zeta(4)$, we can mimic Euler's idea and look at roots at $\pm \pi, \pm i \pi,\pm 2 \pi, \pm 2 i \pi,\pm 3 \pi, \pm 3 i \pi$.

Let $$p(z) = \left(1 - \left(\frac{z}{i \pi}\right)^4 \right) \times \left(1 - \left(\frac{z}{2 i \pi}\right)^4 \right) \times \left(1 - \left(\frac{z}{3 i \pi}\right)^4 \right) \times \cdots$$

It is not hard to guess that $p(z)$ is same as $$\frac{i \sin(z) \times \sin \left( \frac{z}{i} \right)}{z^2} = \left(1-\frac{z^2}{3!} + \frac{z^4}{5!} -\cdots \right) \times \left(1+\frac{z^2}{3!} + \frac{z^4}{5!} + \cdots \right)$$

Compare the coefficient of $z^4$ to get $$\zeta(4) = \frac{\pi^4}{90}$$

This proof could be extended for any even number to give that $$\zeta(2n) = (-1)^{n+1} \frac{B_{2n} 2^{2n}}{2(2n)!} \pi^{2n} $$

As expected for odd numbers, this doesn't work. For instance for $3$, if you try to work out by looking at $$p(z) = \left(1 - \left(\frac{z}{\omega \pi}\right)^3 \right) \times \left(1 - \left(\frac{z}{2 \omega \pi}\right)^3 \right) \times \left(1 - \left(\frac{z}{3 \omega \pi}\right)^3 \right) \times \cdots$$ where $\omega^3 = 1$ there is an asymmetry since $$\sin(z) \sin \left( \frac{z}{\omega}\right) \sin \left( \frac{z}{\omega^2}\right)$$ extends on both sides and the non-zero roots are at $$\pm \pi,\pm \omega \pi,\pm \omega^2 \pi,\pm 2 \pi,\pm 2 \omega \pi,\pm 2 \omega^2 \pi,\pm 3 \pi,\pm 3 \omega \pi,\pm 3 \omega^2 \pi,\ldots$$ and hence the $\zeta(3)$ terms nicely hides by canceling out and the resulting expression only gives $\zeta(6)$.

Answer 4

Knowing a close form for $\zeta(2)$ there is an algebraic way to get $\zeta(4)$.

Consider $f(m,n):=\dfrac{2}{mn^3}+\dfrac{1}{m^2n^2}+\dfrac{2}{m^3n}$

There is the identity:

$f(m,n)-f(m,n+m)-f(m+n,n)=\dfrac{2}{m^2n^2}$

Therefore:

$\displaystyle \sum_{m,n>0} f(m,n)-\sum_{m,n>0} f(m,n+m)-\sum_{m,n>0} f(m+n,n)=\sum_{m,n>0} \dfrac{2}{m^2n^2}$

The right member is equal to:

$\displaystyle \sum_{m=1}^{+\infty}\Big(\sum_{n=1}^{+\infty}\dfrac{2}{m^2n^2}\Big)=2\sum_{m=1}^{+\infty}\dfrac{1}{n^2}\Big(\sum_{n=1}^{+\infty}\dfrac{1}{m^2}\Big)=2\Big(\sum_{n=1}^{+\infty}\dfrac{1}{n^2}\Big)\Big(\sum_{n=1}^{+\infty}\dfrac{1}{m^2}\Big)=2\zeta(2)^2$

The second sum in the left member is equal to:

$\displaystyle \sum_{n>m>0} f(m,n)$

The third one is equal to:

$\displaystyle \sum_{m>n>0} f(m,n)$

Therefore the left member is equal to:

$\displaystyle \sum_{n=1}^{+\infty}f(n,n)=\sum_{n=1}^{+\infty}\dfrac{5}{n^4}=5\zeta(4)$

(proof found in "Quelques conséquences surprenantes de la cohomologie de $SL_2(\mathbb{Z})$, Don Zagier) http://people.mpim-bonn.mpg.de/zagier/files/tex/ConsequencesCohomologySL/fulltext.pdf

Answer 5

From How many ways to calculate: $\sum_{n=-\infty}^{+\infty}\frac{1}{(u+n)^2}$ where $u \not \in \Bbb{Z}$, we know that $$ \sum_{n=-\infty}^\infty \frac{1}{(z+n)^2}=\frac{\pi^2}{\sin^2(\pi z)}. $$ Differentiating this twice, we have $$ \sum_{n=-\infty}^\infty \frac{1}{(z+n)^4}=\frac{\pi^4(2+\cos(2\pi z))}{3\sin^4(\pi z)}. $$ So $$ \sum_{n=1}^\infty \left(\frac{1}{(z-n)^4}+\frac{1}{(z+n)^4}\right)=\frac{\pi^4(2+\cos(2\pi z))}{3\sin^4(\pi z)}-\frac{1}{z^4}. $$ Note that the LHS of the above is analytic $z=0$ and hence $$ \sum_{n=1}^\infty\frac{1}{n^4}=\lim_{z\to 0}\frac{1}{2}\left(\frac{\pi^4(2+\cos(2\pi z))}{3\sin^4(\pi z)}-\frac{1}{z^4}\right)=\frac{\pi^4}{90}. $$，

Answer 6

Consider the contour integral $$ \oint_C\frac{\pi\cot\pi z}{z^4}\ dz $$ where $C$ is the counter-clockwise square contour centered at origin with vertices $\left(N+\frac12\right)(\pm1\pm i)$.

---

Lemma

Suppose that the function $\phi(z)$ is holomorphic at $z=n\in\mathbb{Z}$ with $\phi(n)\neq0$, then $\pi\phi(z)\cot\pi z$ has a simple pole at $n$ with residue $\phi(n)$.

Proof

Note that $\tan\pi z$ have simple zeros at $z=n$, hence $\pi\phi(z)\cot\pi z$ have simple poles there and $$ \text{Res}\left[\pi\phi(z)\cot\pi z\ ;\ n\right]=\text{Res}\left[\frac{\pi\phi(z)}{\tan\pi z}\ ;\ n\right]=\frac{\pi\phi(n)}{\pi\sec^2\pi n}=\phi(n). $$

---

Thus, by residue theorem for $z\neq0$ we obtain $$ \sum_{n=-N}^N\text{Res}\left[\frac{\pi\cot\pi z}{z^4}\ ;\ z=n\right]=\sum_{n=-N,\ n\neq0}^N\frac1{n^4}=2\sum_{n=1}^N\frac1{n^4}.\tag1 $$ From the Taylor series of $\cot\pi z$ at $z=0$ we obtain \begin{align} \frac{\pi\cot\pi z}{z^4}&=\frac\pi{z^4}\cos\pi z\csc\pi z\\ &=\frac\pi{z^4}\left(1-\frac{(\pi z)^2}{2!}+\frac{(\pi z)^4}{4!}-\frac{(\pi z)^6}{6!}+\cdots\right)\left(\frac1{\pi z}+\frac{\pi z}{6}+\frac{7(\pi z)^3}{360}+\cdots\right)\\ &=\frac1{z^5}\left(1-\frac{(\pi z)^2}{2!}+\frac{(\pi z)^4}{4!}-\frac{(\pi z)^6}{6!}+\cdots\right)\left(1+\frac{(\pi z)^2}{6}+\frac{7(\pi z)^4}{360}+\cdots\right)\\ \end{align} Expanding the series above, we see that $$ \text{Res}\left[\frac{\pi\cot\pi z}{z^4}\ ;\ z=0\right]=-\frac{\pi^4}{2!\cdot6}+\frac{\pi^4}{4!}+\frac{7\pi^4}{360}=-\frac{\pi^4}{45}.\tag2 $$ Observe that at any point on the boundary, we have $$ \left|\frac{\pi\cot\pi z}{z^4}\right|\le\frac{\pi\coth\frac\pi2}{\left(N+\frac12\right)^4}.\tag3 $$

---

Proof

Putting $z=x+iy$ and using the trigonometric sum formulas and basic identities, we have $$ |\cot\pi z|^2=\left|\frac{\cos\pi z}{\sin\pi z}\right|=\frac{\sinh^2\pi y+\cos^2\pi x}{\cosh^2\pi y-\cos^2\pi x}. $$ On the vertices sides of contour $C$, we have $x=\pm\left(N+\frac12\right)$ giving $\cos\left(N+\frac12\right)\pi=0$, hence $$ |\cot\pi z|=|\tanh\pi y|\le1. $$ On the horizontal sides we have $0\le\cos^2\pi x\le1$, hence $$ |\cot\pi z|^2\le\frac{\sinh^2\pi y+1}{\cosh^2\pi y-1}=\frac{\cosh^2\pi y}{\sinh^2\pi}=\coth^2\pi y. $$ Therefore $$ |\cot\pi z|\le\coth\pi y=\coth\left(N+\frac12\right)\pi\le\coth\frac\pi2 $$ Thus, on the boundary of contour $C$ we have $$ |\cot\pi z|\le\max\left[1,\coth\frac\pi2\right]=\coth\frac\pi2 $$

---

From $(3)$ and the property $$ \left|\int_C f(z)\ dz\right|\le ML, $$ where $M$ is $\max|f(z)|$ on C and $L$ is the length of $C$, we obtain $$ \oint_C\frac{\pi\cot\pi z}{z^4}\ dz\le\frac{\pi\coth\frac\pi2}{\left(N+\frac12\right)^4}\cdot8\left(N+\frac12\right)=\frac{8\pi\coth\frac\pi2}{\left(N+\frac12\right)^3}\to0 $$ as $N\to\infty$. Thus, using $(1)$ and $(2)$ also using residue theorem we obtain \begin{align} \lim_{N\to\infty}\frac{1}{2\pi i}\oint_C\frac{\pi\cot\pi z}{z^4}\ dz&=0\\ \sum_{n=-\infty}^\infty\text{Res}\left[\frac{\pi\cot\pi z}{z^4}\ ;\ z=n\right]+\text{Res}\left[\frac{\pi\cot\pi z}{z^4}\ ;\ z=0\right]&=0\\ 2\sum_{n=1}^\infty\frac1{n^4}-\frac{\pi^4}{45}&=0\\ \large\color{blue}{\sum_{n=1}^\infty\frac1{n^4}}&\large\color{blue}{=\frac{\pi^4}{90}}. \end{align}

Answer 7

Here is a probabilistic proof. Start with the integral

\begin{align} I=\int_{0}^{1} ... \int_{0}^{1} \frac{1}{1-x^2_1 \ ... \ x^2_4} \ dx_1 \ ... \ dx_4. \end{align}

Convert the integrand into a geometric series, use Tonelli's Theorem to exchange summation and integration, and integrate term by term to get the sum

\begin{align} \sum_{n=0}^{\infty} \frac{1}{(2n+1)^4}. \end{align}

By expanding $\zeta(4)$ into \begin{align} \zeta(4) & =\sum_{n=1}^{\infty} \frac{1}{(2n)^4} + I \\ & = \frac{1}{16} \zeta(4) +I, \end{align} we see \begin{align} \zeta(4)= \frac{16}{15} \sum_{n=0}^{\infty} \frac{1}{(2n+1)^4}. \end{align}

Reconsidering $I,$ make the change of variables (discovered by Beukers, Calabi, and Kolk)
\begin{align} x_i= \frac{\sin \left(\frac{\pi}{2} u_i \right)}{\cos \left(\frac{\pi}{2} u_{i+1} \right)} \end{align} for each $i \in \lbrace 1, \ ... \ 4 \rbrace$ and $u_{4+1} := u_1.$ Such a transformation has a Jacobian Determinant \begin{align} \left | \frac{\partial(x_1,\ ... \ x_4)}{\partial(u_1,\ ... \ u_4)} \right |=\left( \frac{\pi}{2} \right)^4 \left( 1-x^2_1 \ ... \ x^2_4 \right), \end{align} and the region of integration is the open polytope \begin{align} \Delta^{4}= \lbrace (u_1, \ ... \ ,u_4) \in \mathbb{R}^4 : u_{i}+u_{i+1} < 1 , u_i>0 , 1 \leq i \leq 4 \rbrace, \end{align} whose proofs can be found in https://pdfs.semanticscholar.org/35be/01e63c0bfd32b82c97d58ccc9c35471c3617.pdf and https://www.maa.org/sites/default/files/pdf/news/Elkies.pdf.

Hence, we see \begin{align} I=\left( \frac{\pi}{2}\right ) ^4 \text{Vol}(\Delta^4). \end{align}

Consider independent random variables $U_1, \ ... \ ,U_4 \sim \text{Unif}(0,1).$ Then we see
\begin{align} \text{Vol}(\Delta^4)= \text{Pr} \left(U_1+U_2, \ ... \ , U_4 + U_1 < 1 \right). \end{align}

First suppose all $U_i < \frac{1}{2}.$ Then we see $U_{i} +U_{i+1}<1$ for each $i,$ which tells us that $\text{Pr} \left(U_1+U_2, \ ... \ , U_4 + U_1 < 1 \right),$ assuming each $U_i < \frac{1}{2},$ is \begin{align} \int_{0}^{\frac{1}{2}} ... \int_{0}^{\frac{1}{2}} \ du_1 \ ... \ du_4 = \frac{1}{16}, \end{align} the volume of the $4$ dimensional cube $\left(0, \frac{1}{2} \right)^4.$

Next, suppose exactly one $U_j \geq \frac{1}{2}.$ Then we see that $U_{j-1},U_{j+1}<1-U_{j}$ and the remaining $U_l<\frac{1}{2}.$ Note that since we have $4$ random variables, there in all $4$ ways this can happen. This tells us that $\text{Pr} \left(U_1+U_2, \ ... \ , U_4 + U_1 < 1 \right),$ assuming exactly one $U_j \geq \frac{1}{2},$ is \begin{align} 4 \int_{\frac{1}{2}}^{1} \int_{0}^{1-u_j} \int_{0}^{1-u_j} \int_{0}^{\frac{1}{2}} \ du_l \ du_{j-1} \ du_{j+1} \ du_j = \frac{1}{12}. \end{align}

Lastly, suppose exactly two $U_j, U_l \geq \frac{1}{2}$ and $U_j \geq U_l.$ Then we see $U_{j-1},U_{j+1}<1-U_j.$ Note that $j$ and $l$ must not be consecutive to one another. There are $2$ ways to choose such pairs $j$ and $l,$ and for each pair, there are $2$ ways of ordering $U_j,U_l,$ so there are $4$ instances of this happening. Thus, we have that $\text{Pr} \left(U_1+U_2, \ ... \ , U_4 + U_1 < 1 \right),$ assuming exactly two $U_j,U_l \geq \frac{1}{2},$ is \begin{align} 4 \int_{\frac{1}{2}}^{1} \int_{0}^{1-u_j} \int_{0}^{1-u_j} \int_{\frac{1}{2}}^{u_j} \ du_l \ du_{j-1} \ du_{j+1} \ du_j = \frac{1}{48}. \end{align} We cannot have more than two random variables simultaneously be at least $\frac{1}{2},$ which would lead to a contradiction to our constraints. Hence, summing the individual probabilities gives \begin{align} \text{Vol}(\Delta^4)= \frac{1}{6}, \end{align} so \begin{align} I= \left( \frac{\pi}{2} \right)^4 \frac{1}{6} = \frac{\pi^4}{96}, \end{align} and \begin{align} \zeta(4)= \frac{16}{15} I = \frac{\pi^4}{90}. \end{align}

Answer 8

This is just a sketch of one of many possible proofs.

Step1. Prove that over the interval $[0,2\pi]$, the function: $$f(x)=\sum_{n=1}^{+\infty}\frac{\cos(nx)}{n^2}$$ is a second degree-polynomial whose graph goes through the points: $$(0,\pi^2/6),\quad (\pi,-\pi^2/12),\quad (2\pi,\pi^2/6).$$

Step2. Deduce from Lagrange interpolation that: $$ f(x) = \frac{\pi^2}{6}-\frac{x(2\pi-x)}{4}.$$

Step3. Apply Parseval's identity to $f(x)$: $$\int_{0}^{2\pi}f(x)^2\,dx = \pi\sum_{n=1}^{+\infty}\frac{1}{n^4}.$$

Step4. Prove, through the second step, that: $$\int_{0}^{2\pi}f(x)^2\, dx = \frac{\pi^5}{90}.$$

Conclusion:

$$\zeta(4)=\sum_{n=1}^{+\infty}\frac{1}{n^4} = \frac{\pi^4}{90}.$$

Answer 9

By induction we can easily prove that for any nonnegative real numbers $a_k$ $$1-\sum_{k=1}^na_k+\sum_{1\le i<j\le n}a_ia_j-\sum_{1\le i<j<k\le n}a_ia_ja_k\le\prod_{k=1}^n(1-a_k)\le1-\sum_{k=1}^na_k+\sum_{1\le i<j\le n}a_ia_j$$ Taking $a_k=\frac{x^2}{k^2\pi^2}$,we get $$1-\frac{x^2}{\pi^2}\zeta_n(2)+\frac{x^4}{\pi^4}\frac{\zeta_n(2)^2-\zeta_n(4)}2-\frac{x^6}{\pi^6}\frac{\zeta_n(2)^3-\zeta_n(6)}{6}\le\prod_{k=1}^n(1-\frac{x^2}{k^2\pi^2})\le1-\frac{x^2}{\pi^2}\zeta_n(2)+\frac{x^4}{\pi^4}\frac{\zeta_n(2)^2-\zeta_n(4)}2$$ Since $\prod\limits_{k=1}^{\infty}(1-\frac{x^2}{k^2\pi^2})=\frac{\sin(x)}x$, by taking $n\to\infty$ $$1-\frac{x^2}{\pi^2}\zeta(2)+\frac{x^4}{\pi^4}\frac{\zeta(2)^2-\zeta(4)}2-\frac{x^6}{\pi^6}\frac{\zeta(2)^3-\zeta(6)}{6}\le1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots\le1-\frac{x^2}{\pi^2}\zeta(2)+\frac{x^4}{\pi^4}\frac{\zeta(2)^2-\zeta(4)}2$$ subtraciting $1-\frac{x^2}{\pi^2}\zeta_n(2)$ $$\frac{x^4}{\pi^4}\frac{\zeta(2)^2-\zeta(4)}2-\frac{x^6}{\pi^6}\frac{\zeta(2)^3-\zeta(6)}{6}\le\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots\le\frac{x^4}{\pi^4}\frac{\zeta(2)^2-\zeta(4)}2$$ dividing by $x^4$ and putting $x=0$ we get $$\frac1{\pi^4}\frac{\zeta(2)^2-\zeta(4)}2=\frac1{5!}$$ and this follows that $\zeta(4)=\frac{\pi^4}{90}$.

Answer 10

Old thread, but one of my favorite methods is to construct a Fourier series that looks more or less like $$f(x)=\sum_{n=1}^\infty \frac{\cos nx}{n^4}$$ Functions which have a finite number of discontinuities in their periodic extension have Fourier coefficients that are $O(n^{-1})$, so functions continuous through their second derivative should have coefficients $O(n^{-4})$. For an even function of $x$, the even derivatives take care of themselves so only the odd derivatives need be forced to $0$ at the endpoints, and the only odd derivative the matters for $\zeta(4)$ is the first. If we consider the fundamental interval to be $[-\pi,\pi]$, such a function would be $$f(x)=\left(x^2-\pi^2\right)^2$$ A slight improvement would be to find the average of $f(x)$ $$\langle f(x)\rangle=\frac1{2\pi}\int_{-\pi}^{\pi}f(x)dx=\frac1{2\pi}\int_{-\pi}^{\pi}\left(x^4-2\pi^2x^2+\pi^4\right)dx=\frac1{2\pi}(2\pi^5)\frac8{15}=\frac{8\pi^4}{15}$$ And subtract it so that $$g(x)=\left(x^2-\pi^2\right)^2-\frac{8\pi^4}{15}$$ has the right kind of continuity and zero average. It's an even function with period $2\pi$ so we can represent it as $$g(x)=\sum_{n=1}^{\infty}a_n\cos nx$$ Then $$\begin{align}\int_{-\pi}^{\pi}g(x)\cos nx\,dx&=\int_{-\pi}^{\pi}\left[\left(x^2-\pi^2\right)^2-\frac{8\pi^4}{15}\right]\cos nx\,dx\\ &=\left[\left(\frac{\left(x^2-\pi^2\right)^2}{n}-\frac{8\pi^2}{15n}-\frac{12x^2-4\pi^2}{n^3}+\frac{24}{n^5}\right)\sin nx\right.\\ &\left.+\left(\frac{4x\left(x^2-\pi^2\right)}{n^2}-\frac{24x}{n^4}\right)\cos nx\right]_{-\pi}^{\pi}\\ &=-\frac{48\pi}{n^4}(-1)^n\\ &=\sum_{k=1}^{\infty}a_k\int_{-\pi}^{\pi}\cos kx\cos nx\,dx\\ &=\sum_{k=1}^{\infty}a_k\pi\delta_{kn}=\pi a_n\end{align}$$ Where we have used tabular integration to accelerate integration by parts, the Sturm-Liouville properties of the Fourier series to evaluate the orthogonality integrals, and the average value of $\cos^2nx$ of $\frac12$ over the interval of width $2\pi$ to evaluate the normalization integrals. Then for $x\in[-\pi,\pi]$, $$\left(x^2-\pi^2\right)^2-\frac{8\pi^4}{15}=-48\sum_{n=1}^{\infty}\frac{(-1)^n}{n^4}\cos nx$$ When $x=\pi$ for example, $$-\frac{8\pi^4}{15}=-48\zeta(4)$$ Which is equivalent to the desired result. With Parseval's theorem we could get $\zeta(8)$ out of this as well.

Answer 11

This one is from Apostol's Mathematical Analysis exercises and should have been available here long ago.

---

Equating imaginary parts on both sides of the equation $$\cos nt+i\sin nt =(\cos t+i\sin t) ^{n} $$ we get $$\sin nt=\sin^{n} t\left\{\binom{n} {1}\cot^{n-1}t-\binom{n}{3}\cot^{n-3}t+\dots\right\}$$ Putting $n=2m+1$ we get $$\sin(2m+1)t=\sin^{2m+1}tP_{m}(\cot^{2}t)$$ where $$P_{m} (x) =\binom{2m+1}{1}x^{m}-\binom{2m+1}{3}x^{m-1}+\dots$$ is a polynomial of degree $m$. From the above it is now clear that the polynomial $P_{m} (x) $ has $m$ distinct roots given by $x_{k} =\cot^{2}(\pi k/(2m+1))$ for $k=1,2,\dots,m$.

The sum of roots is clearly $$\dfrac{{\displaystyle \binom{2m+1}{3}} } {{\displaystyle \binom{2m+1}{1}}} =\frac{m(2m-1)}{3}$$ and sum of square of roots is $$\left(\frac{m(2m-1)}{3}\right) ^{2}-\frac{m(2m-1)(m-1)(2m-3)}{15}=\frac{m(2m-1)(4m^{2}+10m-9)}{45}$$ Thus we have the identities $$\sum_{k=1}^{m}\cot^{2}\frac{\pi k} {2m+1}=\frac{m(2m-1)}{3}\tag{1}$$ and $$\sum_{k=1}^{m}\cot^{4}\frac{\pi k} {2m+1}=\frac{m(2m-1)(4m^{2}+10m-9)}{45}\tag{2}$$ Next we square and take reciprocal of the inequality $\sin x <x<\tan x$ for $x\in(0,\pi/2)$ to get $$\cot^{2}x<\frac{1}{x^{2}}<1+\cot^{2}x$$ Further squaring gives us $$\cot^{4}x<\frac{1}{x^{4}}<1+2\cot^{2}x+\cot^{4}x$$ Putting $x=\pi k/(2m+1)$ for $k=1,2,\dots,m$ in above equation and adding these equations we get via $(1),(2)$ $$\frac{m(2m-1)(4m^{2}+10m-9)}{45}<\frac{(2m+1)^{4}}{\pi^{4}}\sum_{k=1}^{m}\frac{1}{k^{4}}<m+\frac{2m(2m-1)}{3}+\frac{m(2m-1)(4m^{2}+10m-9)}{45}$$ Dividing the above by $(2m+1)^{4}$ and letting $m\to\infty $ we get the desired result via Squeeze Theorem.

Answer 12

On the proofs of the Basel problem page there is one "peculiar" answer which counts the number of integer solutions to $a^2+b^2+c^2+d^2=n$ as a function of $n$. This is an analog to that answer. Let $r_8(n)$ denote the number of integer solutions to $$a^2+b^2+c^2+d^2+w^2+x^2+y^2+z^2=n$$

We are interested in interpreting $\sum_{n=1}^x r_8(n)$. One way is to think of it as an approximation of the $8$-dimensional ball which has volume $\frac{\pi^4}{24}x^4$ and the other is to exploit a formula for $r_8(n)$ to examine the asymptotic behavior of $\sum_{n=1}^x r_8(n)$.

We will need that $\sum_{n=1}^x \sigma_k(x) \approx \frac{\zeta(k+1)} {k+1}x^{k+1}$ to make this precise we may say that $$\lim_{x\to\infty}{\frac{k+1}{x^{k+1}}\sum_{n=1}^x{\sigma_k(n)}}=\zeta(k+1)$$ I think that this can be seen with just a slight rewriting of this.

From equation (12) of this paper we can write

$r_8(n)=16\sigma_3(n)-32\sigma_3(n/2)+256\sigma_3(n/4)$

Now equipped with $\sum_{n=1}^x\sigma_3\big(\frac{n}{a}\big)\approx \frac{\zeta(4)}{4}\big(\frac{x}{a}\big)^4$

We may write that $$\begin{align} &\frac{\pi^4}{24}x^4 \\ &\approx&\sum_{n=1}^x r_8(n) \\ &=&16\sum_{n=1}^x {\sigma_3(n)} &-32\sum_{n=1}^x {\sigma_3\bigg(\frac{n}{2}\bigg)} &+256\sum_{n=1}^x {\sigma_3\bigg(\frac{n}{4}\bigg)}\\ &\approx &16 \frac{\zeta(4)}{4}x^4 &-32\frac{\zeta(4)}{4}\bigg(\frac{x}{2}\bigg)^4 &+256 \frac{\zeta(4)}{4}\bigg(\frac{x}{4}\bigg)^4 \\ &=x^4\zeta(4)\frac{15}{4} \end{align}$$

So we have that as we let $x$ grow large

$$\frac{\pi^4}{24}x^4 \approx \frac{15}{4}\zeta(4)x^4$$

So then we can conclude that $\zeta(4)=\pi^4/90$

Answer 13

Here is the old school way:

So we have,

$\frac{\sin{x}}{x} = \Pi_{n = 1}^\infty{(1- \frac{x^2}{\pi^2n^2})}$ $ = (1-\frac{x^2}{\pi^2})(1-\frac{x^2}{\pi^22^2})(1-\frac{x^2}{\pi^23^2})(1-\frac{x^2}{\pi^24^2}) \ldots \infty \space \space \space \rightarrow (1)$

To evaluate $\zeta(4)$, we have to evaluate the "sum of product co-efficients of $x^2$-terms taken two at a time" of $(1)$

Considering the the sum of that product ($S$) only,

$$S = \left(\frac{1}{\pi^2}.\frac{1}{2^2\pi^2} + \frac{1}{\pi^2}.\frac{1}{3^2\pi^2} + \frac{1}{\pi^2}.\frac{1}{4^2\pi^2} + \ldots \right)\\ + \left(\frac{1}{2^2\pi^2}.\frac{1}{3^2\pi^2} + \frac{1}{2^2\pi^2}.\frac{1}{4^2\pi^2} + \frac{1}{2^2\pi^2}.\frac{1}{5^2\pi^2} + \ldots \right)\\ + \left(\frac{1}{3^2\pi^2}.\frac{1}{4^2\pi^2} + \frac{1}{3^2\pi^2}.\frac{1}{5^2\pi^2} + \frac{1}{3^2\pi^2}.\frac{1}{6^2\pi^2} + \ldots \right)\\ +\ldots \infty $$

$\implies S = \frac{1}{\pi^4}\left[ (\frac{1}{1^22^2} + \frac{1}{1^23^2} + \frac{1}{1^24^2} + \ldots) + (\frac{1}{2^23^2} + \frac{1}{2^24^2} + \ldots) + \ldots\right] \space \space \ldots (2)$

Simplifying again, $$S = \frac{1}{\pi^4}\left[ \left( \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \ldots \right) \\ + \frac{1}{2^2}\left(\frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \ldots\right) \\ + \frac{1}{3^2}\left(\frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \ldots\right) \\ + \ldots \infty \right]$$

By using the fact that $\zeta(2) = \frac{\pi^2}{6}$, we can re-write the above as,

$$S = \frac{1}{\pi^4}\left[ (\frac{\pi^2}{6} - \frac{1}{1^2} ) \\+ \frac{1}{2^2}(\frac{\pi^2}{6} - \frac{1}{1^2} - \frac{1}{2^2}) \\+ \frac{1}{3^2}(\frac{\pi^2}{6} - \frac{1}{1^2} - \frac{1}{2^2} - \frac{1}{3^2}) \\+ \ldots\right]$$ Simplifying this again, $$S = \frac{1}{\pi^4} \left[ \sum_{n=1}^{\infty}{\frac{1}{n^2}\left(\frac{\pi^2}{6 }-\sum_{m=1}^n{\frac{1}{m^2}}\right)} \right] $$ $ = \frac{1}{\pi^4} \left[ \frac{\pi^2}{6}\sum_{n=1}^{\infty}{\frac{1}{n^2}} - \sum_{n=1}^{\infty}{\left( \frac{1}{n^2}\sum_{m=1}^{n}{\frac{1}{m^2}}\right)}\right]$

$S =\frac{1}{\pi^4}\left[\frac{\pi^4}{36} - K\right] \space\space\ldots (3)$

Simplifying $K$,

$K = \sum_{n=1}^{\infty}{\left( \frac{1}{n^2}\sum_{m=1}^{n}{\frac{1}{m^2}}\right)}$

$ = \frac{1}{1^2}\frac{1}{1^2} + (\frac{1}{2^2}\frac{1}{1^2} + \frac{1}{2^4}) + (\frac{1}{3^2}\frac{1}{1^2} + \frac{1}{3^2}\frac{1}{2^2} + \frac{1}{3^4}) + \ldots $

$ = (\frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \ldots) + \left[ (\frac{1}{1^22^2} + \frac{1}{1^23^2} + \frac{1}{1^24^2} + \ldots) + (\frac{1}{2^23^2} + \frac{1}{2^24^2} + \ldots) + \ldots\right]$

Using $(2)$ we get,

$K = \sum{\frac{1}{n^4}} + \pi^4S = I + \pi^4S\space \space \ldots (4)$

...where $I$ is the sum we are interested in.

Substituting $(4)$ in $(3)$,

$S = \frac{1}{\pi^4}\left[\frac{\pi^4}{36} - (I +\pi^4S) \right] $

$ = \frac{1}{36} - \frac{I}{\pi^4} - S$

$\implies 2S = \frac{1}{36} - \frac{I}{\pi^4}$

But we know the value of $S$ from the taylor expansion of $\frac{sin(x)}{x}$, i.e., $S = \frac{1}{120}$ (by comparing the co-efficients of $x^4$)

Hence, solving for $I$ we get,

$$\boxed{I = \frac{\pi^4}{90}}$$

Answer 14

I would like to present you a method based on Daners' derivation of $\zeta(2)$ (which I summarised on MathStackexchange in here couple years ago).

We start defining (for all $n \in \mathbb{N}_0$)

\begin{align} A_n & =\int_0^{\pi/2}\cos^{2n}x\;\mathrm{d}x,\\ B_n& =\int_0^{\pi/2}x^2\cos^{2n}x\;\mathrm{d}x,\\ C_n& =\int_0^{\pi/2}x^4\cos^{2n}x\;\mathrm{d}x \end{align}

and let $\beta_n = B_n/A_n$ and $\gamma_n = C_n/A_n$.

The first integral for $A_n$ is well known and follows a reccurence relation

$$A_{n}=\frac{2n-1}{2n}A_{n-1}\tag{1}.$$

By applying per partes on the $A_n$ integral twice, we get:

$$A_n=\int_0^{\pi/2}\cos^{2n}x\;\mathrm{d}x=x\cos^{2n}x\bigg{|}_0^{\pi/2}-\frac{x^2}{2}(\cos^{2n}x)'\bigg{|}_0^{\pi/2}+\frac{1}{2}\int_0^{\pi/2}x^2(\cos^{2n}x)''\;\mathrm{d}x$$

The first two terms vanish, so only the integral remains and since $(\cos^{2n}x)''=2n(2n-1)\cos^{2n-2}x-4n^2\cos^{2n}x$, we get for $n\geq 1$:

$$A_n=(2n-1)nB_{n-1}-2n^2B_{n}\tag{2}$$

Similarly, applying per partes twice on $B_n$ instead, we get

$$B_n=\frac16 (2n-1)nC_{n-1}-\frac13 n^2C_{n}\tag{3}$$

Inserting $(1)$ into $(2)$ and $(3)$ and rearranging, we get a following recurence reltions

$$\frac{1\cdot 2}{4}\frac{1}{n^2}=\beta_{n-1}-\beta_n\tag{4}$$ $$\frac{3\cdot 4}{4}\frac{\beta_n}{n^2}=\gamma_{n-1}-\gamma_n\tag{5}$$

Summing these up, we get, by the telescoping property

$$\sum_{l=1}^k\frac{1}{2l^2}=\beta_0-\beta_k \qquad \text{and} \qquad \sum_{k=1}^n\frac{3\beta_k}{k^2}=\gamma_0-\gamma_n. \tag{6}$$

Inserting one sum into another (expressing $\beta_k$), we get $$3\beta_0\sum_{k=1}^n\frac{1}{k^2} - \frac32\sum_{k=1}^n\frac{1}{k^2}\sum_{l=1}^k\frac{1}{l^2}=\gamma_0 - \gamma_n. \tag{7}$$

Note that in general $$2\sum_{k=1}^n a_k\sum_{l=1}^k a_l = 2\sum_{1\leq l \leq k \leq n}a_k a_l = \left(\sum_{k=1}^n a_k\right)^2+\sum_{k=1}^n a_k^2,$$

substituing for $a_k = 1/k^2$ into $(7)$ and rewriting $\sum_{k=1}^n 1/k^2$ as $2\beta_0 - 2\beta_n$ everywhere, we get

$$\bbox[10px,#ffd]{\sum_{k=1}^n \frac{1}{k^4} = 4\beta_0^2 - 4\beta_n^2 - \frac{4}{3}\gamma_0 + \frac{4}{3}\gamma_n.}\tag{8}$$

However, using the inequalities $x^4<(\pi/2)^2 x^2$ and $\frac{2x}{\pi}<\sin x$ valid on $(0,\frac{\pi}{2})$ and by $(1)$, we get

$$0<\gamma_{n-1} <\left(\frac{\pi}{2}\right)^2\beta_{n-1} < \frac{\int_0^{\pi/2}\sin^2x\cos^{2n-2}x}{\int_0^{\pi/2}\cos^{2n-2}x}=\frac{A_{n-1} - A_n}{A_n} = \frac{1}{2n}.$$

Applying the squeeze theorem, we get $$\lim_{n\rightarrow \infty} \beta_n = \lim_{n\rightarrow \infty} \gamma_n = 0$$

and hence, taking the limit of $(8)$,

$$\zeta_4 = \lim_{n\rightarrow \infty} \sum_{k=1}^n\frac{1}{k^4} = 4\beta_0^2-\frac{4}{3}\gamma_0 = 4\left(\frac13 \frac{\pi^2}{2^2}\right)^2-\frac{4}{3} \frac{1}{5}\frac{\pi^4}{2^4} = \frac{\pi^4}{90}$$

This finishes the proof.

Answer 15

by using Fourier series of $f(x)=1, x\in[0,1]$ $$1=\sum_{n=1,3,5,..}^\infty\frac{4}{n\pi}\sin (n\pi x)$$

take triple integrals as follows $$\int_{0}^{1}\int_{0}^{x}\int_{0}^{x}1.dxdxdx=\int_{0}^{1}\int_{0}^{x}\int_{0}^{x} \sum_{n=1,3,5,..}^\infty\frac{4}{n\pi}\sin (n\pi x) dxdxdx$$ $$\frac{1}{6}=\sum_{n=1,3,5,..}^\infty\frac{2}{(n\pi)^2}-\frac{8}{(n\pi)^4}$$ $$\frac{\pi^4}{6}=\sum_{n=1,3,5,..}^\infty\frac{2\pi^2}{n^2}-\frac{8}{n^4}$$ We know that $$\sum_{n=1,3,5,..}^\infty\frac{1}{n^2}=\frac{\pi^2}{8}$$ so $$\frac{\pi^4}{96}=\sum_{n=1,3,5,..}^\infty\frac{1}{n^4}$$ then we use the inequality series $$\sum_{n=1}^\infty\frac{1}{n^4}=\sum_{n=1}^\infty\frac{1}{(2n-1)^4}+\sum_{n=1}^\infty\frac{1}{(2n)^4}$$ simplify it to get $$\sum_{n=1}^\infty\frac{1}{n^4}=\frac{16}{15}\sum_{n=1}^\infty\frac{1}{(2n-1)^4}$$ so, $$\sum_{n=1}^\infty\frac{1}{n^4}=\frac{16}{15}\frac{\pi^4}{96}=\frac{\pi^4}{90}$$

Answer 16

Let $ f(x)=x^2-\frac{1}{12} $ defined on $ [-\frac{1}{2},-\frac{1}{2}) $, and extend $ f $ to be periodic on $ \mathbb{R} $.

We compute that \begin{align*} \hat f(0)=\int_{-1/2}^{1/2}f(x)dx=\int_{-1/2}^{1/2}\left(x^2-\frac{1}{12}\right)dx=0. \end{align*} And for $ k\ne 0 $: \begin{align*} \hat f(k)&=\int_{-1/2}^{1/2}f(x)e^{-2\pi ikx}dx=\int_{-1/2}^{1/2}\left(x^2-\frac{1}{12}\right)e^{-2\pi ikx}dx=\int_{-1/2}^{1/2}x^2e^{-2\pi ikx}dx\\ &=-\left.\frac{x^2e^{-2\pi i kx}}{2\pi ik}\right|_{-1/2}^{1/2}+\frac{1}{\pi ik}\int_{-1/2}^{1/2}xe^{-2\pi ikx}dx=\frac{1}{\pi ik}\int_{-1/2}^{1/2}xe^{-2\pi ikx}dx\\ &=\frac{1}{2\pi^2k^2 }\int_{-1/2}^{1/2}xd(e^{-2\pi ikx})=\left.\frac{1}{2\pi^2k^2}xe^{-2\pi ikx}\right|_{-1/2}^{1/2}+\frac{1}{2\pi^2k^2}\int_{-1/2}^{1/2} e^{-2\pi ikx}dx=\frac{(-1)^k}{2\pi^2k^2}. \end{align*}

By the Parseval identity \begin{align*} \int_{-1/2}^{1/2}|f(x)|^2dx=\sum_{k=-\infty}^{\infty}|\hat{f}(k)|^2=|\hat{f}(0)|^2+2\sum_{k=1}^{\infty}|\hat{f}(k)|^2=\sum_{k=1}^{\infty}\frac{1}{2\pi^4 k^4}. \end{align*} On the other hand, \begin{align*} \int_{-1/2}^{1/2}|f(x)|^2dx&=\frac 1{180}. \end{align*} Hence, we have $$ \sum_{k=1}^{\infty}\frac{1}{k^4}=\frac{\pi^4}{90}. $$

Answer 17

we use Plancherel Theorem to prove it

for any function $f\in{C(\mathbb{R}/\mathbb{Z}; \mathbb{C})}$, and any integer $n\in{\mathbb{Z}}$, we define the $n^{th}$ Fourier coefficient of $f$, denoted $\hat{f}(n)$, by the formula

$\hat{f}(n):=\langle f,e_{n} \rangle=\int_{0}^{1}f(x)e^{-2πinx}dx$

and the trigonometric Fourier coefficients $a_n$, $b_n$ for $n = 0, 1, 2, 3, ...$ by

$a_{n}:=2\int_{[0,1]}f(x)cos(2πnx)dx$;$b_{n}:=2\int_{[0,1]}f(x)sin(2πnx)dx$

and the series $\frac{1}{2}a_0+\sum\limits_{n=1}^{∞}(a_{n}cos(2πnx)+b_{n}sin(2πnx))$ converges in $L^2$ metric to $f$

we can immediately get $a_{n}=\hat{f}(n)+\hat{f}(-n)$, $b_{n}=i(\hat{f}(n)-\hat{f}(-n))$

$\hat{f}(±n)=\frac{1}{2}(a_n±\frac{b_n}{i})$

$||f||_{2}^{2}=|\hat{f}(0)|^2+\sum\limits_{n=1}^{∞}(|\frac{1}{2}(a_n+\frac{b_n}{i})|^2+|\frac{1}{2}(a_n-\frac{b_n}{i})|^2)$

$=|\hat{f}(0)|^2+\frac{1}{4}\sum\limits_{n=1}^{∞}((a_n+\frac{b_n}{i})(\overline{a_n}-\frac{\overline{b_n}}{i})+(a_n-\frac{b_n}{i})(\overline{a_n}+\frac{\overline{b_n}}{i}))$

$=|\hat{f}(0)|^2+\frac{1}{4}\sum\limits_{n=1}^{∞}(|a_n|^2-\frac{a_{n}\overline{b_n}}{i}+\frac{b_{n}\overline{a_n}}{i}+|b_n|^2+|a_n|^2+\frac{a_{n}\overline{b_n}}{i}-\frac{b_{n}\overline{a_n}}{i}+|b_n|^2)$

$=|\hat{f}(0)|^2+\frac{1}{4}\sum\limits_{n=1}^{∞}2(|a_n|^2+|b_n|^2)$

Let f(x) be the function defined by $f(x) = (1- 2x)^2$ when $x\in[0, 1)$, and extended to be $\mathbb{Z}$-periodic for the rest of the real line

$a_{n}=\frac{4}{π^{2}n^{2}}$ for $n≥1$, $b_n=0$, $a_{0}=\frac{2}{3}$

$\int_{0}^{1}(1-2x)^{4}dx=\frac{1}{9}+\frac{1}{2}\sum\limits_{n=1}^{∞}((\frac{4}{π^{2}n^{2}})^2+0)$

$\frac{(2x-1)^{5}|_{0}^{1}}{5×2}=\frac{1}{9}+\frac{1}{2}\frac{16}{π^4}\sum\limits_{n=1}^{∞}\frac{1}{n^4}$

$\sum\limits_{n=1}^{∞}\frac{1}{n^4}=(\frac{1}{5}-\frac{1}{9})\frac{π^4}{8}=\frac{π^4}{90}$

q.e.d

Answer 18

I derive an intermediate formula for the sum for the general case of $\zeta (2k)$, then specialise to the case $\zeta(4)$ and evaluate it. Then use the formula to evaluate the general case in terms of Bernoulli numbers. First, note

\begin{align*} \sum_{n=1}^\infty \dfrac{1}{n^{2k}} & = \frac{1}{(2k-1)!} \sum_{n=1}^\infty \dfrac{1}{n^{2k}} \int_0^\infty e^{-y} y^{2k-1} dy \nonumber \\ & = \frac{1}{(2k-1)!} \sum_{n=1}^\infty \int_0^\infty e^{-nx} x^{2k-1} dx \nonumber \\ & = \frac{1}{(2k-1)!} \int_0^\infty \dfrac{x^{2k-1}}{e^{x} - 1} dx \nonumber \\ & = \frac{1}{(2k)!} \int_0^\infty \dfrac{x^{2k} e^x}{(e^x - 1)^2} dx \nonumber \\ & = \frac{1}{2 \cdot (2k)!} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x - 1)^2} dx . \end{align*}

where we have performed an integration by parts and extended the range of integration. We can write the final integral in a way that is amenable to complex integration, with an identity. Note

\begin{align*} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x - 1)^2} dx - \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x + 1)^2} & = \int_{-\infty}^\infty \dfrac{4 x^{2k} e^{2x}}{(e^{2x} - 1)^2} dx \nonumber \\ & = \int_{-\infty}^\infty \dfrac{2^{-2k+1} (2x)^{2k} e^{2x}}{(e^{2x} - 1)^2} 2dx \nonumber \\ & = 2^{-2k+1} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x - 1)^2} dx \end{align*}

implying

\begin{align*} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x - 1)^2} dx = \frac{1}{1- 2^{-2k+1}} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x + 1)^2} \end{align*}

So

\begin{align*} \sum_{n=1}^\infty \dfrac{1}{n^{2k}} & = \frac{1}{2 \cdot (2k)!} \frac{1}{1- 2^{-2k+1}} \int_{-\infty}^\infty \dfrac{x^{2k} e^x}{(e^x + 1)^2} \end{align*}

We can write

\begin{align*} \sum_{n=1}^\infty \dfrac{1}{n^{2k}} & = \frac{1}{2 \cdot (2k)!} \frac{1}{1- 2^{-2k+1}} \left. \frac{\partial^{2k}}{\partial \alpha^{2k}} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} \right|_{\alpha=0} \qquad (1) \end{align*}

where $-\frac{1}{2} \leq \alpha \leq \frac{1}{2}$. We now evaluate this integral using complex analysis. Consider the rectangular contour, $C$, in the figure

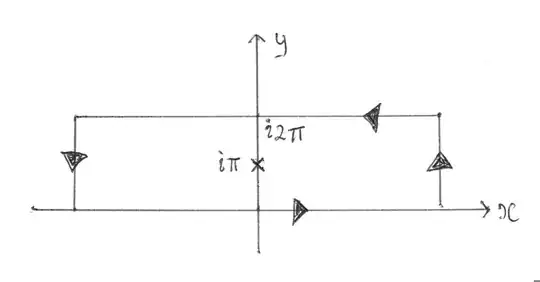
and the integral

\begin{align*} \oint_C \dfrac{e^{\alpha z} e^z}{(e^z + 1)^2} dz \end{align*}

whose integrand has a pole at $\pi i$. The integral along the vertical edges vanishes as:

\begin{align*} f(z) = \dfrac{e^{\alpha (x+iy)} e^{(x+iy)}}{(e^{x+iy} + 1)^2} = \begin{cases} e^{- (1 - \alpha) (x+iy)} & x \rightarrow \infty \\ e^{(1 + \alpha) (x+iy)} & x \rightarrow - \infty \\ \end{cases} \end{align*}

So that

\begin{align*} \oint_C \dfrac{e^{\alpha z} e^z}{(e^z + 1)^2} dz & = \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x - 1)^2} dx - e^{i 2 \alpha \pi} \int_{-\infty + i 2 \pi}^{\infty + i 2 \pi} \dfrac{e^{\alpha x} e^x}{(e^x - 1)^2} dx \nonumber \\ & = (1 - e^{i 2 \alpha \pi}) \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} dx . \end{align*}

Which rearranged is

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} dx & = \frac{2 \pi i}{1 - e^{i 2 \alpha \pi}} \frac{1}{2 \pi i} \oint_C \dfrac{e^{\alpha z} e^z}{(e^z + 1)^2} dz \nonumber \\ & = \frac{2 \pi i}{1 - e^{i 2 \alpha \pi}} Res_{z=\pi i} [f(z)] . \end{align*}

We calculate the residue. Expand about pole, $z_0 = i \pi$:

\begin{align*} \frac{1}{(e^z + 1)^2} & = \frac{1}{(e^{z_0 + (z-z_0)} - e^{z_0})^2} \nonumber \\ & = e^{-2 z_0} \dfrac{1}{[(z-z_0) + \frac{1}{2!} (z-z_0)^2+ \cdots]^2} \nonumber \\ & = e^{-2 z_0} \dfrac{1}{(z-z_0)^2 [(1 + \frac{1}{2!} (z-z_0)+ \cdots]^2} \nonumber \\ & = e^{-2 z_0} \dfrac{1}{(z-z_0)^2 [1 + (z-z_0) + \cdots]} \nonumber \\ & = e^{-2 z_0} \dfrac{1}{(z-z_0)^2} [(1 - (z-z_0) + \cdots] \nonumber \\ & = e^{-2 z_0} \dfrac{1}{(z-z_0)^2} - e^{-2 z_0} \dfrac{1}{z-z_0} + \cdots \end{align*}

Using this we can find the residue:

\begin{align*} \frac{e^{\alpha z} e^z}{(e^z + 1)^2} & = e^{- 2 z_0} \dfrac{ e^{(\alpha + 1) z_0 + (\alpha + 1) (z-z_0)} }{ (z-z_0)^2 } - e^{- 2 z_0} \dfrac{ e^{(\alpha + 1) z_0} }{ z-z_0 } + \cdots \nonumber \\ & = e^{- 2 z_0} \dfrac{ e^{(\alpha + 1) z_0} [1 + (\alpha + 1) (z-z_0) + \cdots] }{ (z-z_0)^2 } - e^{- 2 z_0} \dfrac{ e^{(\alpha + 1) z_0} }{ z-z_0 } + \cdots \nonumber \\ & = e^{- 2 z_0} \dfrac{ e^{(\alpha + 1) z_0} }{ (z-z_0)^2 } + e^{- 2 z_0} \dfrac{ \alpha e^{(\alpha + 1) z_0} }{ z-z_0 } + \cdots \end{align*}

So that

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{\alpha x} e^x}{(e^x + 1)^2} dx & = \frac{2 \pi i}{1 - e^{i 2 \alpha \pi}} \cdot \alpha e^{i (\alpha + 1) \pi} \nonumber \\ & = \frac{\alpha \pi}{\sin( \alpha \pi)} . \end{align*}

Using this in $(1)$,

\begin{align*} \sum_{n=1}^\infty \dfrac{1}{n^{2k}} & = \frac{1}{2 \cdot (2k)!} \frac{1}{1- 2^{-2k+1}} \left. \frac{\partial^{2k}}{\partial \alpha^{2k}} \frac{\alpha \pi}{\sin( \alpha \pi)} \right|_{\alpha=0} \qquad (2) \end{align*}

This is the general formula I mentioned at the beginning.

Case: $k=2$

We specialise to the case $k=2$. We expand in $\alpha$,

\begin{align*} \frac{\alpha \pi}{\sin( \alpha \pi)} & = \frac{1}{ 1 - \frac{1}{3!} (\alpha \pi)^2 + \frac{1}{5!} (\alpha \pi)^4 - \cdots } \nonumber \\ & = 1 + \frac{1}{6} \alpha^2 \pi^2 - \frac{1}{120} (\alpha \pi)^4 + \frac{1}{6^2} (\alpha \pi)^4 + \cdots \nonumber \\ & = 1 + \frac{1}{6} \alpha^2 \pi^2 + \frac{7}{360} \alpha^4 \pi^4 + \cdots \end{align*}

Using this in (2),

\begin{align*} \zeta (4) = \sum_{n=1}^\infty \dfrac{1}{n^4} & = \frac{1}{2 \cdot 4!} \frac{1}{1- 2^{-3}} \frac{7}{15} \pi^2 \nonumber \\ & = \frac{\pi^2}{90} \end{align*}

General case:

We have the series expansion of $x \pi \csc x \pi$ in terms of Bernoulli numbers:

\begin{align*} \frac{ x \pi }{ \sin( x \pi) } = \sum_{n=0}^\infty \dfrac{ 2 (2^{2n-1} - 1) (-1)^{n+1} \pi^{2n} B_{2n} }{ (2n)! } x^{2n} . \end{align*}

Using this in $(2)$,

\begin{align*} \zeta (2k) = \sum_{n=1}^\infty \dfrac{1}{n^{2k}} & = \frac{1}{2 \cdot (2k)!} \frac{1}{1- 2^{-2k+1}} \left. \frac{\partial^{2k}}{\partial \alpha^{2k}} \frac{\alpha \pi}{\sin( \alpha \pi)} \right|_{\alpha=0} \nonumber \\ & = \frac{1}{2 (1- 2^{-2k+1})} \cdot \dfrac{ 2 (2^{2k-1} - 1) (-1)^{n+1} \pi^{2k} B_{2k} }{ (2k)! } \nonumber \\ & = \dfrac{ (-1)^{k+1} B_{2k} (2\pi)^{2k} }{ 2(2k)! } \end{align*}

Answer 19

The way I know it is by a formula for $\zeta(2n)$ that comes from the Fourier series of $f_z(t):=\cos(tz)$ for $z\in\Bbb C\setminus\Bbb Z$ (to me this is a very nice way to see it but I dont know if it would be enough nice for you).

We start with the Fourier series of the $2\pi$-periodic extension of

$$f_z:[-\pi,\pi]\to\Bbb R,\quad t\mapsto\cos(tz),\quad z\in\Bbb C\setminus \Bbb Z$$

defined by

$$\mathrm Sf_z(t)=\frac{\sin(\pi z)}{\pi}\left(\frac1z+\sum_{k= 1}^\infty(-1)^k\left(\frac1{z+k}+\frac1{z-k}\right)\cos(k t)\right)\tag{1}$$

(the above is easy to get so I will not show these steps.)

From $(1)$ setting $t=\pi$ we can obtain a series for the cotangent when $z\in\Bbb C\setminus\Bbb Z$

$$\pi\cot(\pi z)=\frac1z+\sum_{k=1}^\infty\left(\frac1{z+k}+\frac1{z-k}\right)\tag{2}$$

And from $(2)$ we get

$$\pi z\cot(\pi z)=1+2z^2\sum_{k=1}^\infty\frac1{z^2-k^2}\tag{3}$$

Now observe that if $|z|\le r<1$ then $|z^2-k^2|\ge n^2-r^2>0$ for $k\in\Bbb N_{>0}$. Then $(3)$ converges in $\Bbb B(0,r)$.

Now observe that we can write $(z^2-k^2)^{-1}$ as a geometric series as

$$\frac1{z^2-k^2}=-\frac1{k^2}\sum_{j=0}^\infty\left(\frac{z^2}{k^2}\right)^j,\quad z\in\Bbb B(0,1), k\in\Bbb N_{>0}\tag{4}$$

Then from $(3)$ and $(4)$ we get the expression

$$\pi z\cot(\pi z)=1-2\sum_{k=1}^\infty\zeta(2k)z^{2k},\quad z\in\Bbb B(0,1)\tag{5}$$

where we used the fact that the double series is summable to exchange the order of summation. Finally we use the following well-known identities to build a different series for the cotangent

$$\frac{z}{e^z-1}=\sum_{k=0}^\infty\frac{B_k}{k!}z^k,\quad \frac{z}{e^z-1}+\frac{z}2=\frac{z}2\coth(z/2),\quad z\in\Bbb C\setminus 2\pi i\Bbb Z\tag{6}$$

where $B_k$ are the Bernoulli numbers. From $(6)$ is easy to derive the following series that represent the cotangent in a neighborhood of zero

$$z\cot z=1+\sum_{k=1}^\infty(-1)^k\frac{4^k}{(2k)!}B_{2k}z^{2k},\quad z\in\Bbb B(0,r)\tag{7}$$

Because the cotangent is analytic then we can compare the coefficients of $(5)$ and $(7)$ getting finally

$$\zeta(2k)=(-1)^{k+1}B_{2k}\frac{(2\pi)^{2k}}{2(2k)!},\quad k\in\Bbb N_{>0}\tag{8}$$

In particular $\zeta(4)=(-1)^3 B_4\frac{(2\pi)^4}{2\cdot 4!}=-B_4\pi^4/3=\pi^4/90$.