Polynomial approximation of circle or ellipse

Question

Trying again, with a somewhat simpler sounding question, since my previous one (Generalizations of equi-oscillation criterion) got zero response:

Let $F:[0,1] \to R^2$ be a parametric polynomial curve of degree $m$. I want to adjust the coefficients of $F$ to make it lie as closely as possible to the unit circle, $C$. More specifically, I want to have $F(0) = (1,0)$, and $F(1) = (0,1)$, and I want the maximum distance $$E_1 = \max \{dist(F(t),C): t \in [0,1]\}$$ to be minimized.

It would be OK to minimize the following error $E_2$ instead, if it's easier:

$$ E_2 = \max \{ \big| F_x^2(t) + F_y^2(t) - 1 \big|: t \in [0,1]\}$$

What if I replace the unit circle by an ellipse (for example).

Two specific questions:

(1) Can we prove that the best approximation is equi-oscillatory, in some sense ?

(2) How can the best approximation be computed ?

This site http://spencermortensen.com/articles/bezier-circle/ has a good result for the case of a circle with ($m=3$).

You could also think of this as a question about Bezier curves of degree $m$. Clearly, it would be a good idea to set the first control point equal to $(1,0)$, and the last one equal to $(0,1)$. Then, we just need to adjust the other control points until we get an optimal fit.

A simple algebraic version of the problem: Find two polynomials $x(t)$ and $y(t)$ such that $x(0)=1$, $x(1)=0$, $y(0)=0$, $y(1)=1$, and $x(t)^2 + y(t)^2 - 1$ is small for all $t \in [0,1]$.

Answer 1

There is a general procedure for a circle that minimizes $\max |p^2+q^2-1|$. In what follows it is convenient to make two slight modifications to your problem:

1. The parameterization will be defined on an interval $[-\alpha, \alpha] \subset [-1,1]$ rather than $[0,1]$.
2. The approximation is for another arc of length $\tfrac{\pi}{2}$.

The first modification is only a parameter substitution and the second a rotation so solving this problem will clearly also solve the original problem.

Let $n > 0$ be some degree. Then we want to find polynomials $p$ and $q$ of degree at most $n$ such that $\max |p^2+q^2-1|$ is minimized over the interval $[-1,1]$. Note that $p^2+q^2-1$ will have degree at most $2n$. It is well known that the Chebyshev polynomial of the first kind $T_{2n}$ solves the minimax problem on $[-1,1]$ among all polynomials of degree at most $2n$ with leading coefficient $2^{2n-1}$. Therefore the best solution would be of the form

$$ p^2+q^2 = 1 + \lambda T_{2n} $$

for some parameter $\lambda \in [0,1)$ that should be as small as possible. Such a solution can indeed be found based on the explicit factorization

$$ \begin{eqnarray} 1 + \frac{T_{2n}(x)}{\cosh(2n\,t)} &=& \frac{2^{2n-1}}{\cosh(2n\, t)} \prod_{k=1}^{2n}\left(x - \cos\left(\tfrac{(2k-1) \pi}{2n} - t\,i\right)\right) \\ &=& \frac{2^{2n-1}}{\cosh(2n\, t)} \prod_{k=1}^{2n}\left(x - \cos\left(\tfrac{(2k-1) \pi}{2n}\right)\cosh(t) - \sin\left(\tfrac{(2k-1) \pi}{2n}\right) \sinh(t)\,i\right) \end{eqnarray}$$

for all $t \in \mathbb{R}$. (See the edit below for a derivation of this factorization.) Since the LHS is a real polynomial, the roots in the expression above have conjugate symmetry. Now take $t > 0$ and define the complex polynomial $r(x)$ of degree $n$ by including only the roots in the upper half plane:

$$ r(x) = \frac{2^n}{\sqrt{2 \cosh(2n\,t)}} \prod_{k=1}^{n}\left(x - \cos\left(\tfrac{(2k-1) \pi}{2n} - t\,i\right)\right).$$

Then $r(-x) = (-1)^n \,\overline{r}(x)$ where $\overline{r}$ means $r$ with conjugated coefficients. Write $r = p + q\,i$ for real polynomials $p$ and $q$ then

$$p^2+q^2 = (p + q\,i)(p - q\, i) = r \,\overline{r} = 1 + \frac{T_{2n}}{\cosh(2n\, t)}.$$ So in fact we found a one-parameter family of good approximations to the circle on the interval $[-1,1]$. (Larger $t$ give better approximations.) The question is what this parameter signifies and which value of $t$ actually solves our problem as stated.

Since all roots of $r$ are in the upper half plane its restriction to $\mathbb{R}$ is a complex curve with strictly increasing argument, so it wraps the real line around the origin in counter clockwise direction. One can show that $p$ and $q$ have degrees $n$ and $n-1$ respectively, both have only real roots and the roots of $q$ separate those of $p$. The parameter $t$ controls how "fast" the curve wraps around the origin, where greater values of $t$ give "slower" curves that stay closer to the unit circle on $[-1,1]$.

The only restrictions that prevent us from taking aribrarily large values of $t$ are that the curve must begin and end on the unit circle and cover an angle of exactly $\tfrac{\pi}{2}$ over some interval contained in $[-1,1]$. The largest zeroes of $T_{2n}$ are $\pm \cos(\tfrac{\pi}{4n})$ so if $\alpha = \cos(\tfrac{\pi}{4n})$ and we restrict $r$ to the interval $[-\alpha, \alpha]$ then at least it begins and ends on the unit circle. Since $r(-\alpha) = (-1)^n \, \overline{r}(\alpha)$ the end point is obtained by reflecting the starting point in the real axis (for even $n$) or imaginary axis (for odd $n$). Therefore if we take $t$ maximal such that $r(\alpha)^2$ is purely imaginary, so $p(\alpha) = \pm q(\alpha)$, then the curve spans an angle of precisely $\tfrac{\pi}{2}$.

To summarize the results of this fairly long story:

1. To get a degree $n$ approximation consider the polynomial $r(x)$ defined above that depends on an auxiliary real parameter $t>0$.
2. Let $\alpha = \cos(\tfrac{\pi}{4n})$. Determine the maximal value $t>0$ for which $r(\alpha)^2 \in i\,\mathbb{R}$.
3. Then $|r(-\alpha)| = |r(\alpha)| = 1$ and $\left|\,|r(x)|^2 - 1\,\right| \leq \tfrac{1}{\cosh(2n \, t)}$ for $x \in [-\alpha, \alpha]$. Moreover $r$ is the best approximation of a quarter circle on the interval $[-\alpha, \alpha]$.

The first few approximations found this way are:

$$ \begin{array}{c|c|c|c} n & \alpha & t & \max \, \left| \, |r|^2-1 \, \right| \\ \hline 1 & 0.70710678 & 0.65847895 & 0.5 \\ 2 & 0.92387953 & 1.2149195 & 0.015505028 \\ 3 & 0.96592583 & 1.5982608 & 0.0001368784 \\ 4 & 0.98078528 & 1.8786122 & 5.9437783 \times 10^{-7} \\ 5 & 0.98768834 & 2.098419 & 1.5406786 \times 10^{-9} \\ 6 & 0.99144486 & 2.2789419 & 2.6561189 \times 10^{-12} \\ 7 & 0.99371221 & 2.4320125 & 3.2665949 \times 10^{-15} \\ 8 & 0.99518473 & 2.5648448 & 3.0106701 \times 10^{-18} \\ 9 & 0.9961947 & 2.6821493 & 2.1570627 \times 10^{-21} \\ 10 & 0.99691733 & 2.7871679 & 1.2359399 \times 10^{-24} \end{array} $$

Edit: Here's how the factorization can be found. The key property is that $$T_{2n}\left(\frac{x+x^{-1}}{2}\right) = \frac{x^{2n}+x^{-2n}}{2}$$ for all $x \neq 0$. So $$1 + \frac{T_{2n}\left(\frac{x+x^{-1}}{2}\right)}{\cosh(2n\,t)} = \frac{2 \cosh(2n\,t) + x^{2n}+x^{-2n}}{2 \cosh(2n\,t)}$$ and this vanishes when $x^{2n} = -e^{\pm 2n \, t}$. The roots are therefore $$ x= \exp\left(\frac{(2k-1)\pi\,i}{2n} \pm t\right)$$ for $k \in \{1, \dotsc, 2n\}$ and for such a root we have $$\frac{x+x^{-1}}{2} = \cos\left(\frac{(2k-1)\pi}{2n}\mp t\, i\right).$$ Since $\cos$ is even this gives $2n$ roots of the polynomial $$1+\frac{T_{2n}}{\cosh(2n \, t)}$$ of degree $2n$. After fixing the proper leading coefficient the factorization follows.

Answer 2

A proposal: Present your circular arc in the form $$\eqalign{ x(t)&={1\over\sqrt{2}}(\cos t-\sin t) ={1\over\sqrt{2}}\left(1-t-{t^2\over2}+{t^3\over6}+{t^4\over 24}-{t^5\over120}-\ldots\right) \cr y(t)&={1\over\sqrt{2}}(\cos t+\sin t) ={1\over\sqrt{2}}\left(1+t-{t^2\over2}-{t^3\over6}+{t^4\over 24}+{t^5\over120}-\ldots\right) \cr}\qquad\left(-{\pi\over4}\leq t\leq{\pi\over4}\right)$$ and use as many terms as are needed for the required precision. The following figure shows an overlay of the exact circle and the above polynomial approximation up to ${t^5\over120}$:

Answer 3

The complete answer may be hard, but contrary to the OP, I see no difficulty in stating the question and generalizing the concept of equi-oscillation to the two-dimensional case. Let $V_n$ denote the affine space of all pairs $v=(x_n,y_n)$ of polynomials each of degree $\leq n$ with $v(0)=(1,0)$ and $v(1)=(0,1)$ . Note that $V_n$ has dimension $2(n-1)$. For $v=(x_n,y_n)\in V$ put

$$ || v ||=\sup_{t\in[0,1]} \bigg| x_n(t)^2+y_n(t)^2-1\bigg| $$

Then define $\mu_n={\sf inf}(|| v |||, v \in V_n)={\sf min}(|| v |||, v \in V_n)$. Say that a $v\in V_n$ is optimal if $||v||=\mu_n$.

Definition Let $\varepsilon>0$. We say that a pair $v=(x_n,y_n)\in V_n$ is $\varepsilon$-oscillating if there is an increasing sequence of $1+{\sf dim}(V_n)$ elements $t_1<t_2< \ldots<t_{1+{\sf dim}(V_n)}$ in $[0,1]$ such that the sequence $w_i=x_n(t_i)^2+y_n(t_i)^2-1$ is alternating (i.e. $w_{i+1}=-w_i$ for all $i$) and $|w_i|=\varepsilon$ for all $i$.

Note that $1+{\sf dim}(V_n)=2n-1$ above.

Conjecture 1 A $v\in V_n$ is optimal if and only if it is $\mu_n$-oscillating.

Conjecture 2 There is a unique optimal solution for each $n$.

Those conjectures are true when $n=2$. Indeed, in this case a generic $v\in V_2$ can be written $$v(a,b,t)=(1-t+at(1-t),t+bt(1-t))$$. Let us also put

$$ F(a,b,t)=1-t+at(1-t))^2+(t+bt(1-t))^2-1 \tag{1} $$

Let $\theta$ be the largest real root of $T=X^4+4X^3-8X^2+8X-4$, so that $\theta$ is approximately $0,85 \ldots$. I claim then that $v(\theta,\theta,.)$ is the unique optimal solution.

Let $G(t)=F(\theta,\theta,t)$ and $$\mu=G(1/2)=\frac{\theta^2}{8}+\frac{\theta}{2}-\frac{1}{2} \approx 0,015 \tag{3} $$

We then have the identities

$$ \mu-G(t)=\big(t-\frac{1}{2}\big)^2 \bigg(\frac{\theta^2}{2}+2\theta-2+2\theta^2t(1-t) \bigg) \tag{4} $$

$$ \mu+G(t)=2\theta^2 \bigg(t(1-t)-\frac{\theta-1}{2\theta^2} \bigg)^2 \tag{5} $$

Note that the polynomial $Q(t)=t(1-t)-\frac{\theta-1}{2\theta^2}$ has two roots in $[0,1]$, $\alpha$ and $1-\alpha$ where $\alpha \approx 0,12 \ldots$. This shows that $G$ is $\mu$-oscillating.

Let $(a,b)$ be any pair such that $||v(a,b,.)|| \leq \mu $. Then

$$ F(a,b,\alpha) \geq -\mu, \ F(a,b,\frac{1}{2}) \leq \mu, \ F(a,b,1-\alpha) \geq -\mu \tag{6} $$

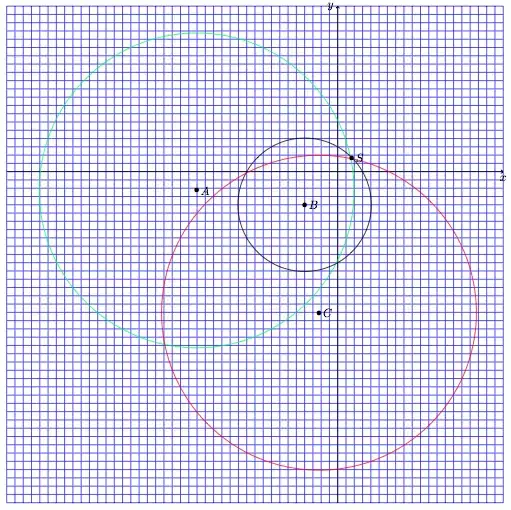
Those three inequalities alone will suffice to force $(a,b)=(\theta,\theta)$, showing optimality and unicity. Indeed, consider in the plane points $A,B,C,S$ with the following coordinates :

$$ A(-\frac{1}{\alpha},-\frac{1}{1-\alpha}), \ B(-2,-2), \ C(-\frac{1}{1-\alpha},-\frac{1}{\alpha}), \ S(\theta,\theta) $$

Also, consider the disk $D_A$ with center $A$ and radius $\frac{\sqrt{\mu}}{\alpha(1-\alpha)}$, the disk $D_B$ with center $B$ and radius $4\sqrt{1+\mu})$, and the disk $D_C$ with center $C$ and radius $\frac{\sqrt{\mu}}{\alpha(1-\alpha)}$.

Then a pair $(a,b)$ satisfies (6) iff the point with such coordinates is inside $D_C$ but outside $D_A$ and $D_B$. The figure below shows that $S$ is the only such point, qed.

Answer 4

Maybe you can get your answer here:

https://www.jimherold.com/computer-science/best-fit-bezier-curve

http://www.google.com.br/url?sa=t&rct=j&q=Optimal+fitting+bezier+curves&source=web&cd=1&cad=rja&ved=0CCsQFjAA&url=https%3A%2F%2Fece.uwaterloo.ca%2F~dwharder%2FMaplesque%2FBezier%2FBestFittingBezierCurves.ppt&ei=tnXxUK_UDZOe8gTko4H4Cw&usg=AFQjCNFfkMNXviJSzFCBIqbTL3EWZcgTpA

http://www.google.com.br/url?sa=t&rct=j&q=Optimal+fitting+bezier+curves&source=web&cd=9&cad=rja&ved=0CGkQFjAI&url=http%3A%2F%2Fwww.dtic.mil%2Fcgi-bin%2FGetTRDoc%3FAD%3DADA350611&ei=tnXxUK_UDZOe8gTko4H4Cw&usg=AFQjCNGW_AP5QddfGugn_5WzoIUDIMJ7ng

Answer 5

As a start, there is the well-known rational exact fit of $(2t/(1+t^2), (1-t^2)/(1+t^2)$. (Because $(2t)^2 + (1-t^2)^2 = 4t^2 + 1 - 2t^2 + t^4 = 1 + 2t^2 + t^4 = (1+t^2)^2$).

If you write $1/(1+t^2) = 1-t^2+t^4 ...\pm t^{2k} ...$, you can get an initial polynomial approximation.