Inverse of elliptic integral of second kind

Question

The Wikipedia articles on elliptic integral and elliptic functions state that “elliptic functions were discovered as inverse functions of elliptic integrals.” Some elliptic functions have names and are thus well-known special functions, and the same holds for some elliptic integrals. But what is the relation between the named elliptic functions and the named elliptic integrals?

It seems that the Jacobi amplitude $\varphi=\operatorname{am}(u,k)$ is the inverse of the elliptic integral of the first kind, $u=F(\varphi,k)$. Or related to this, $x=\operatorname{sn}(u,k)$ is the inverse of $u=F(x;k)$. It looks to me as if all of Jacobi's elliptic functions relate to the elliptic integral of the first kind. For other named elliptic functions listed by Wikipedia, like Jacobi's $\vartheta$ function or Weierstrass's $\wp$ function, it is even harder to see a relation to Legendre's integrals.

Is there a way to express the inverse of $E$, the elliptic integral of the second kind, in terms of some named elliptic functions? I.e. given $E(\varphi,k)=u$, can you write a closed form expression for $\varphi$ in terms of $k$ and $u$ using well-known special functions and elementary arithmetic operations?

In this post the author uses the Mathematica function FindRoot to do this kind of inversion, but while reading that post, I couldn't help wondering whether there is an easier formulation. Even though the computation behind the scenes might in fact boil down to root-finding in any case, it feels like this task should be common enough that someone has come up with a name for the core of this computation.

Answer 1

$\def\E{\operatorname E} \def\F{\operatorname F} \def\I{\operatorname I}$Quantile Function

Mathematica already had inversebetaregularized $\I^{-1}_z(a,b)$ which is a quantile function for the beta distribution. Although the question is about solving E$(x,m)=a$, there are Mathematica closed forms solving $\E(x,m)+c\F(x,m)=a$

1. With the second lemniscate constant L$_2$:

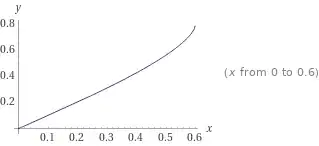
$$\E(x,2)=a\implies x=\frac12\sin^{-1}\left(\sqrt{\text I^{-1}_{\frac a{\text L_2}}\left(\frac12,\frac34\right)}\right),0\le a\le\text L_2$$

which is correct.

2. Note Elliptic D$(x,m)$:

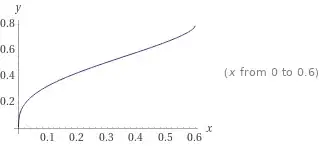
$$\E(x,-1)-\F(x,-1)=\operatorname D(x,-1)=a\implies x=\sin^{-1}\left(\sqrt[4]{\text I^{-1}_{\frac a{\text L_2}}\left(\frac34,\frac12\right)}\right),0\le a\le \text L_2$$

which is correct.

3.

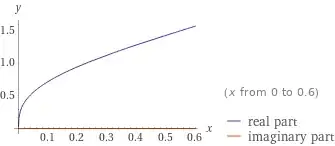
$$\E(x,2)-\frac12\sin(2x)\cos^\frac32(2x)=a\implies x=\frac12\sin^{-1}\left(\sqrt{\I^{-1}_{\frac a{\text L_2}}\left(\frac32,\frac34\right)}\right),0\le a\le \text L_2$$

which also works

4. Using the Baxter constant B:

$$\operatorname E(z,\sqrt[-3]{-1})-\left(\frac12+\frac i{2\sqrt3}\right)\operatorname F(z,\sqrt[-3]{-1}) =a\implies z=\sin^{-1}\left(\frac{\sqrt[12]{-1}}{\sqrt[4]3}\sqrt{1-\sqrt[3]{\operatorname I^{-1}_{1-\sqrt[4]3\sqrt[3]4\sqrt[12]{-1}\text Ba}\left(\frac23,\frac12\right)}}\right),0\le \sqrt[12]{-1}a\le \frac1{\sqrt[4]3\sqrt[3]4\text B}$$

shown here

Real part:

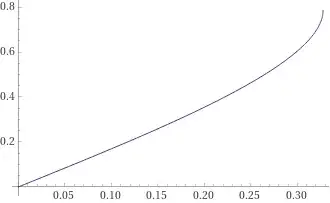
Imaginary part:

There are also other special cases, but they are very specific and may not have applications. The $\text I^{-1}_z(a,b)$ function also expresses many special cases of Jacobi elliptic functions. Also use the periodic nature of the elliptic integrals to find values outside of the $a$ restriction.

---

Series Solution

The simplest recurrence relation for the coefficients seems to be from inverting:

$$f(z)=\E(\sin^{-1}(\sqrt z),m)=\frac12\int_0^z\sqrt{\frac{mt-1}{t(t-1)}}dt\implies y(z)=f^{-1}(z)$$

The differential equation and $f(z)’s$ series are:

$$y’=2\sqrt{\frac{y(y-1)}{my-1}}\iff4y=4y^2+y’^2-my’^2y\\f(z)=\sqrt z+O(z^\frac32)\implies y=\sum_{n=1}^\infty a_nz^{2n},a_1=1$$

Substituting and equating powers of $z^{2n}$ using Kronecker delta, we get:

$$\sum_{n=1}^\infty a_n x^{2n}=\sum_{k=1}^\infty\sum_{j=1}^\infty a_ka_jx^{2k+2j}+\sum_{k=1}^\infty\sum_{j=1}^\infty a_ka_jkjx^{2k+2j-2}-m\sum_{k=1}^\infty\sum_{j=1}^\infty\sum_{p=1}^\infty a_ka_ja_pkjx^{2k+2j+2p-2}\\ a_n=\sum_{k=1}^\infty\sum_{j=1}^\infty a_ka_j\delta_{n,k+j}+\sum_{k=1}^\infty\sum_{j=1}^\infty a_ka_jkj\delta_{n,k+j-1}-m\sum_{k=1}^\infty\sum_{j=1}^\infty\sum_{p=1}^\infty a_ka_ja_pkj\delta_{n,k+j+p-1} $$

Next, we apply $\delta_{n,m}$’s sifting property. Now $a_n$ depends on $a_n$, so subtract the $k=1$ causing it and substitute $k\to k+1$ to get:

$$\bbox[2px,border:2px solid blue]{\E(y,m)=z\implies \sin^2(y)=\sum_{n=1}^\infty a_n z^{2n};(1-2n)a_n=a_{n-1}+\sum_{k=1}^{n-2}a_{n-k}(a_k+a_{k+1}(k+1)(n-k))-m\sum_{k=1}^{n-1}\sum_{j=1}^{n-k}a_ka_ja_{n-k-j+1}kj\\=\left\{1,\frac{m-1}3,\frac{m-1}{45}(11m-2),\frac{m-1}{315}(74m^2-29m+1),\frac{m-1}{14175}(3548m^3-2220m^2+249m-2),\frac{m-1}{467775}(136883m^4-117818m^3+24474m^2-1016m+2),\dots\right\}}$$

which matches $f(x)$’s series reversion. A series directly inverting $\E(x,m)$ requires expanding a $\sin^2(y)$ as a series which requires finding another recurrence. The series works for $z,m\in\Bbb C$. The series here can be used to expand the formulas in the “Quantile Function” section too.

Answer 2

There is a routine for an inverse Elliptical Integral of the second kind published by J.P. Boyd. See https://sci-hub.se/10.1016/j.amc.2011.12.021

He uses a brute force approach. He firstly makes an empirical guess (initialization) of the result and then checks the accuracy and adjusts it by Newton's iteration, and does it again. His routine only calls E(phi,k) three times.

I modified it for C++, which can be easily changed for Python. Please feel free to use. As I have fast routines for E(phi,k) I let the iterations limit be 10 as a safety measure. Occasionally the iteration decreases to a small amount near the tolerance and then oscillates about that amount. Indeed one could add an escape clause when this oscillation occurs, which on my computer is 1.1*10^-16 (double significant precision). Typically the iterations vary from 3 to 7 to achieve the above accuracy. Of course this method depends upon the accuracy of E(phi,k)

I tried using the same technique for an inverse Elliptical Integral of the Third kind, a modification of Newtons iteration is relativity simple. However the initialization is a problem. I cannot get it to rapidly approach the solution. I note Boyd's comment in his paper "This emphasizes a crucial point: the true criterion of merit for an initialization is not that it is close to the solution, but only that it is a point from which Newton’s iteration can find its way rapidly to the solution"

Name: InverseElliptic2
Language: C++
Description: This function performs the inverse to the Legendre elliptic Integral of the 2nd kind E(phi,k). This function concerns an ellipse having a major axis of length a and minor axis of length b. The ellipse is orientated such the major poles are located at (a,0) and (-a,0) and the minor poles are located at (0,b) and (0,-b). The purpose of this function is to find the angle phi corresponding to the distance s along the curve of an ellipse commencing at B(0,b) and continuing along the curve of the ellipse towards a point P(x,y) between (0,b) and (a,0). The angle phi is that angle measured between the point B and (0,0) and P. The function takes as one of the arguments z where z= s/C where s is the length of the arc along the ellipse from B to P and as such it values ranges from 0 <= s <= C, where C is one quarter of the circumference of the ellipse, and thus z ranges from 0 <= z <= 1. The other argument is the modulus k, the modulus ranges from 0 < k < 1. The function returns the angle phi corresponding to the arc BP for a "unit ellipse" for modulus k.

double Elliptical_Integrals::iellip2( double z, double k) {

double r =0.0;
double zeta =0.0; 
double theta = 0.0;
double iE =0.0;
double prev_iE=0.0;
double m =0.0;
double mu = 0.0;
unsigned int i = 0;
double tol = 1.111e-16;
m = kk;
mu = 1-m;
zeta = 1 - (z/complete_elliptical_integral_2nd_kind(k));

r = sqrt( zetazeta + mumu );
theta = atanf( mu/( z + 1.0e-12)); 
iE= (PI/2.0) + sqrt(r)(theta - (PI/2.0));
i=0;
do{
    prev_iE= iE;
    iE = prev_iE - ((ellip2( prev_iE,k)-z)/(sqrt( 1 - pow(k,2)*pow(sin(prev_iE),2) )));
    i++;
    if ( i > 10)

        break;
}while ( abs(iE-prev_iE) > tol);
return iE;

}

Answer 3

I've just found a physical problem (in classical mechanics) involving the trajectory of a particle in which I had to take the inverse of $E(\phi,k)$, the incomplete elliptic integral of the 2nd kind. For the elliptic integral of the 1st kind $F(x,k)$ this is an easy task beacuse the Jacobi elliptic function $sn(x,k)$ (or JacobiSN(x,k) in mathematical software) is just $F^{-1}(x,k)$. However, currently there is no built-in function for the inverse of $E(\phi,k)$. My computational solution was then to build a procedure for the inverse, using FindRoot (in Mathematica9.0) or fsolve (in Maple 2015). F.M.S. Lima (University of Brasilia).

Answer 4

I know this isn't a closed form, but I was interested in this question and have found one can relate the two functions together as series representations. I have written a short article here but this is the crux of it

Write \begin{equation} E(\phi,k) = \sum_{i=0}^\infty \frac{Q_i(k)}{(2i-1)!}\phi^{2i-1} \end{equation} where $Q_i(k)$ are polynomials in $k$, from the series expansion here we can get a finite form for these polynomials as \begin{equation} Q_n(m) = 2(-4)^n\sum_{k=1}^n \frac{(2k-3)!!}{k!}\left(\frac{-m}{8}\right)^k \sum_{j=0}^{k-1} \binom{2k}{j}(-1)^{1-j}(j-k)^{2n}, \;\;\; n>0 \end{equation} with $Q_0(k)$ defined as $1$. Then you can write the inverse series using series reversion in a very similar manner to $E(\phi,k)$ \begin{equation} \phi(E,k) = \sum_{i=0}^\infty \frac{R_i(k)}{(2i-1)!}E^{2i-1} \end{equation} where the relation between the new polynomials $R_i(k)$ is given by the explicit reversion formula found at the bottom of this link, giving \begin{equation} R_n(k) = (2n)! \sum_{\tau_n=n}(-1)^{\sigma_n} \frac{\prod_{i=1}^{\sigma_n}2n+i}{\prod_{j=1}^n k_j!}\prod_{l=1}^n \left(\frac{Q_l(k)}{(2l+1)!}\right)^{k_l} \end{equation} where $\sigma_n=k_1+k_2+k_3+\cdots+k_n$, and $\tau_n=k_1+2k_2+3k+3+\cdots + nk_n$ and the sum is over all sets of indices $k_i$ that meet the requirement $\tau_n=n$. I don't know if any nice simplifications or tricks can be made to reduce this to a functional form. The only numerical element here is converging the series to the desired accuracy.