In a small programming exercise I asked myself, I want to calculate various things about ellipses. The part I'm stuck with is the following: I want to calculate the angle that is needed cor covering a given distance on the circumference of a given ellipse, while starting on a given angle. This image should illustrate the problem:
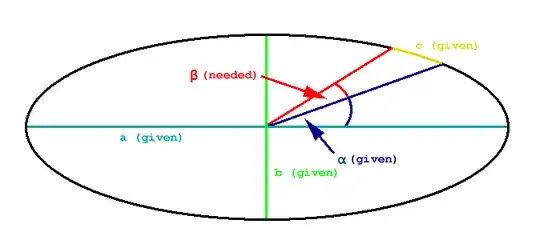
It is guaranteed that α < 90°, but it is possible that α+β > 90°
I would like to do this only with mathematical operations that are available in 'general' programming languages (like C++, e.g. those in cmath). So, while calculating the actual result in my program, I would like to avoid integrals or derivatives. Although the result will probably less exact without these operations, it should have maximum deviation of ~5%.