I was asked to find out the simplicial homology groups of the torus $T=S^1\times{}S^1$ embedded in $R^3$. I triangulated the torus like this :
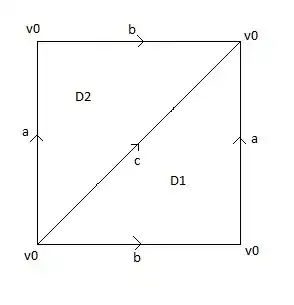
Here the $0$-simplices are $\{v_0\}$. $1$-simplices are $\{a,b,c\}$ and the $2$-simplices are $\{D_1,D_2\}$. And I found out the homology groups : $H_0(T)=\mathbb{Z}, H_1(T)=\mathbb{Z}^2,H_2(T)=\mathbb{Z}$
But my teacher said it was wrong, because the triangulation is not correct. According to her it should be:
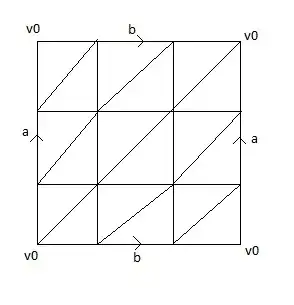
I don't understand what is wrong with my triangulation of the torus $T$. Can someone please clarify this to me? Thanks! (Excuse the crude pictures!)