2

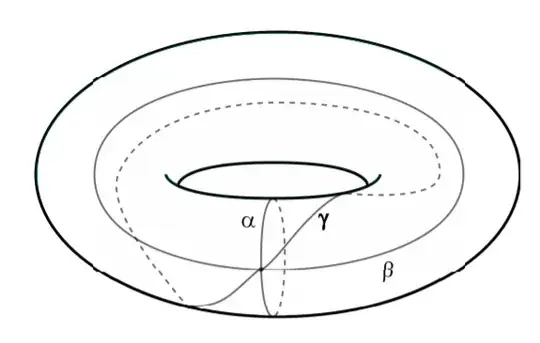
In the paper, it is said that Figure 1.1 in Example 1.2.3 is a triangulation of a torus.

enter image description here

How to see that every face in this triangulation is an triangle? How many triangles are there in this triangulation? It is a little hard to see this directly.

Thank you very much.

LJR
  • 14,870

1 Answers1

3

This is the same as

enter image description here

under the usual identifications. But beware, I think it depends on the definitions, but usually this is not considered as a valid triangulation of a torus. For example see here (roughly it depends on the fact that the triangulation only has to be a CW-complex or a simplicial complex). To answer your question, there are either $0$ or $2$ triangles.

Community
  • 1
TheGeekGreek
  • 8,158
  • thank you very much. If we require that the triangulation to be a CW-complex, then there is no triangles? What are the differences between a CW-complex and a simplicial complex? – LJR Feb 03 '17 at 20:02
  • A CW complex is much more general than a simplicial complex, i.e. under the right definitions the geometric realization of a simplicial complex is a (regular) CW-decomposition. I am currently practicing for my first topology exam, so maybe I am not the biggest topologist, but as far as I understood, in a CW-complex you speak about cells, they can be triangles but it is a bit more abstract. – TheGeekGreek Feb 03 '17 at 20:14
  • @LJR I just asked my assistant in topology if it is a CW-complex for sure. Will write you in a while. You're welcome. – TheGeekGreek Feb 03 '17 at 20:19