2

Yesterday, my teacher gave us an example of triangulation of torus($18$ triangles) without gave us the exactly definition of triangulation and told us if you want to know more, just read book about algebraic topology. So I look for at least 5 books about algebraic topology probably, each of them give the definition of triangulation by homeomorphism mapping from a underlying space of simplicial complex to surface, I can understand what is this mean. However, they soon give me an example of triangulation of torus by using $18$ triangles without give me what is homeomorphism mapping betweet them which is really confusing me at first. Fortunately, I find Elements of Algebraic Topology written by Munkres, and he told me the graph we draw with labels is an abstruct simplicial complex, more specifically, it follows the definition he gave.enter image description here

By this definiton I can understand why the graph we draw is a triangulation of torus. Then, I wonder why two triangles can not be a triangulation of torus. Please allow me to tell you how I understand this question: actually this graph can not be represent any abstract simplicial complex, since if it can be an abstract simplicial complex, the vertex set is a one-point set like this $\{a\}$, and it has a simplex like $\{a,a,a\}$, because it is a triangle in our graph, but it can not be a simplex by definiton of simplex, so it can not be an abstract simplicial complex. 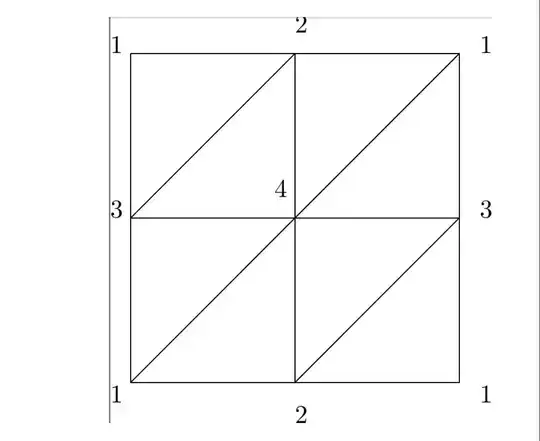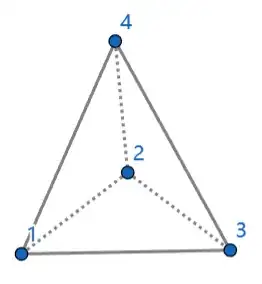And I find another example that can not be a triangulation of torus.The graph is like belowenter image description here. This is an answer about why it can not be a triangulathion. But I do not understand what is mean he said(I don't understand why them intersect in just the edge $13$ and vertex $4$, why not triangle 134), actually I don't understand almost every question about why this is a triangulation of something or that is not a triangulation of something on mathstackexchange. I think about this question like this: It can be represent an abstruct simplicial complex, and one of its geometry realization like this enter image description here .

But it's homeomorphic to $S^2$, so it can not be a triangulation of torus. However that answer seems to tell me it can't be a (abstract or geometric) simplicial complex which is different from what I thought.

And my questions are:

$1$.Is the proof of why $18$ triangles is a triangulation of torus correct?

$2$.I think there must have another understanding of the graph we try to give a triangulation of something, maybe the books and answers by others think the graph as geometric simplicial compelx rather than an abstract simplicial complex，but how can you get homeomorphism mapping from that, what's the graph meaning we draw, how can we get homeomorphism mapping by just give a graph.

$3$.What's wrong with my discussion about the last two triangulation, I think it can be answerd by the answer of question 2, maybe I misunderstand what Munkres said, can we infer it can't be an abstract simplicial complex if two triangles with three distinct vertices are marked with the same notation(like 134 and 134 in the second picture I post above)

PS:

$1$. I am a stupid student, please give me details about what you saying as long as you can. Please!

$2$. I have not much understanding about CW complex.

$3$. If you have another understanding about graph we draw that different from abstract simplicial complex, and if it is very geometrically, please state it by using the language of algebra, for example when we say glue the upper side and below side, it is say that we are constructing the quotient topology space of $I\times I$ equivalently

MGIO
  • 105
  • A triangulation is not a picture, the picture just helps. A triangulation of a space $X$ is a family of continuous maps $\Delta^n\to X$ (where $n$ will vary) satisfying some axioms. If you like it is gluing data that tells you how to build $X$ from putting these "triangles" or "simplices" (continuous images of $\Delta^n$) next to each other. – FShrike Apr 07 '24 at 12:28
  • 1
    Unfortunately what those axioms are, differs from author to author. You could consider: (abstract) simplicial complexes, Delta complexes or (geometric realisations of) simplicial sets as your fundamental notion and these have different constraints. Simplicial sets is the most flexible – FShrike Apr 07 '24 at 12:31
  • You can triangulate the torus with just two triangles. In the Delta-complex/simplicial set formulation. But iirc the simplicial complex formulation would disallow this triangulation for not having distinct edges or something like that – FShrike Apr 07 '24 at 12:32
  • 1
    P.S. you're not a stupid student – FShrike Apr 07 '24 at 12:33
  • this this this this this – FShrike Apr 07 '24 at 12:35

0 Answers0