0

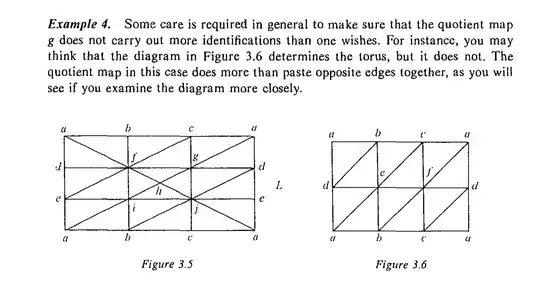
Below it is possible to find an extract from Chapter 1.3 of Munkres' "Elements of Algebraic Topology", which concerns the triangulation of the torus.

enter image description here

I have the following question regarding Figure 3.5: do we really need $af$, $fh$, $hj$, and $ja$?
Indeed, I have in mind other triangulations of the torus where all these segments are missing.

Every feedback will be (more than) greatly appreciated, since I find all this truly impenetrable.

Thank you for your time!

Kolmin
  • 4,249
  • 1
    Does this post address your question? – Lee Mosher Dec 20 '21 at 17:13
  • 1
    If you want to discard $af, fh, hj, ja$, then you need to consider $db, ce$ i.e., a triangulation of torus having $9$ vertices, $18$ triangles, and $27$ edges is possible. While triangulating you need to keep this in mind: In a simplicial complex, the intersection of two simplices is either empty or a single common face of them. In other words, the intersection of two simplices as a union of common faces not giving a single common face is out of consideration. – Sumanta Dec 20 '21 at 18:35
  • @LeeMosher: Not directly, but reading it has proved to be extremely useful nonetheless. Thanks! – Kolmin Dec 21 '21 at 18:33
  • @User: I completely overlooked that the triangulation I was hinting at does contain $db$ and $ce$ as you pointed out. Thanks a lot also for the remaining points! – Kolmin Dec 21 '21 at 18:33
  • 1
    @User: Now, general question, somewhat hidden in the main question: the triangulation you are referring to and the one in Munkres are two triangulations, but it should be absolutely irrelevant which one we pick, right? As long as two are simplicial complexes representing the same object, everything works exactly the same from an homological standpoint, right? – Kolmin Dec 21 '21 at 18:36

0 Answers0