This isn't (and really, can't be) a complete answer, just an eclectic list of examples (often relying on standard properties, and not proven here) that may be counterintuitive on first glance.
From the answers to the linked question, two smooth manifolds are diffeomorphic if "they cannot be distinguished by their smooth structures." Throughout, $n$ denotes a positive integer.
Examples
Any two (non-empty) contractible open subsets of Cartesian $n$-space are diffeomorphic. Particularly, the open unit disk, an open rectangle, and the Cartesian plane are mutually diffeomorphic. Note carefully that diffeomorphisms need not extend (and if they do extend, need not extend as diffeomorphisms) to the boundaries.
In a similar spirit, if we remove from the Cartesian plane (i) the origin, (ii) the interval $[-1, 1]$ on the horizontal axis, (iii) the closed unit disk, (iv) the closed rectangle $[-1, 1] \times [-1, 1]$, etc. etc., the remaining sets are mutually diffeomorphic.
A once-punctured $n$-sphere is diffeomorphic to Cartesian $n$-space. Stereographic projection is a convenient way to prove this. Generally, if $M$ is a connected manifold and $p$, $q$ are arbitrary points of $M$, the complements $M\setminus\{p\}$ and $M\setminus\{q\}$ are diffeomorphic (in fact, are diffeomorphic through isotopies from the identity map). Intuitively, fix a path from $p$ to $q$, drag the puncture smooth from $p$ to $q$, and smoothly carry along a small ball, leaving fixed everything outside a thin tube around the path. (In more detail, first show any two punctured coordinate balls are diffeomorphic by a diffeomorphism fixing a neighborhood of the boundary, then cover the path by coordinate balls, use compactness to select a finite subcover, and proceed inductively.)
A Möbius strip with its central circle removed is diffeomorphic to a punctured disk. This is the simplest example of what algebraic geometers call "blowing up," and a good self-test of "[Can] I look at two surfaces and see if they diffeomorphic?"
The reflection map $(x, y) \mapsto (x, -y)$ induces a diffeomorphism of the unit circle to itself, but this diffeomorphism is not induced by "deforming the circle within itself", or even "within the plane." If we prefer complex numbers, complex conjugation is a diffeomorphism on the set of unit complex numbers.
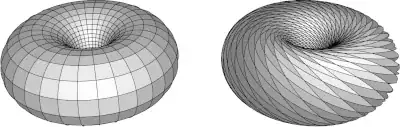
If we cut open a torus along a meridian obtaining a cylinder, twist the cut end by an integer number of turns, and reglue the cut ends of the cylinder, we obtain a self-diffeomorphism of the torus that is not isotopic to the identity:
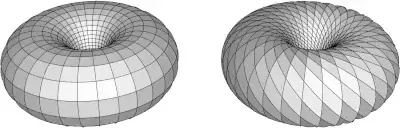
That is, diffeomorphisms are more general than the popular-topology cliché of "deforming a space like a lump of clay." Particularly, a diffeomorphism may appear to contravene the pop-top rule "without cutting or gluing." Informally, we can "cut temporarily" so long as we "reglue everything back exactly as we found it."
Among mathematicians, no cutting is involved at all, just mapping. Here we may view the torus as the quotient of the Cartesian plane by the integer lattice. The diffeomorphism $(x, y) \mapsto (x, nx + y)$ of the plane sends every translate of the integer lattice to itself, and therefore induces a diffeomorphism of the quotient torus. Generally, if $a$, $b$, $c$, $d$ are integers with $ad - bc = \pm1$, the linear diffeomorphism $(x, y) \mapsto (ax + by, cx + dy)$ of the plane induces a diffeomorphism of the torus.
Any two knotted circles in Cartesian $3$-space are diffeomorphic. (Their complements need not be.)
Classification theorems are useful in large part because they reduce the question "Are these two manifolds diffeomorphic?" to an easier question: "Do these two manifolds have the same (computable) topological invariants?" Particularly, two compact, connected smooth surfaces are diffeomorphic if and only if they have the same Euler characteristic (see also genus) and are both orientable or both non-orientable. For example:
- Costa's surface visibly is orientable and has three ends, and with a bit of thought has genus $1$; it is therefore diffeomorphic to a torus with three punctures.
- The set of complex lines through the origin in the complex Cartesian plane is easily seen to be a surface parametrized by complex slope, the complex version of $m \leftrightarrow (y = mx)$. The vertical line has infinite slope. The set of complex lines, a.k.a. the complex projective line, is therefore (for some value of therefore) the one-point compactification of the complex plane, a.k.a., the Riemann sphere. (As an aside, many interesting manifolds arise as quotients under group actions. The torus and projective spaces are "nice" examples. Vexing things can occur, e.g., the quotient of the punctured plane under the action $f^{\pm}_{t}(x, y) \mapsto \pm(e^{t} x, e^{-t} y)$ is the (non-Hausdorff) line with two origins. To see why, identify each real number $m$ with the hyperbola $xy = m$, and examine carefully what happens on the punctured axes, where $m = 0$.)
Non-Examples
An open $n$-ball and a punctured $n$-ball are not diffeomorphic. Probably no surprises here, though the only proofs I know use (co-)homology.
The image of a manifold under a smooth bijection need not inherit the topology of the image, and need not be a manifold. Classic examples include
- An irrational winding on a torus, the image of a line $t \mapsto (t, \alpha t)$ of irrational slope $\alpha$ under the quotient of the Cartesian plane by the integer lattice;
- The figure-8 curve $t \mapsto (\sin t, \sin 2t)$, $-\pi < t < \pi$.

