Assume you have a torus. Cut it at some place to make a cylinder. Twist one end of the cylinder 360 degrees. Glue the ends back together. Is this "twisted" torus different topologically than a regular torus?
-
1(1) By itself , the twisted torus is the same as the original torus. (2) But if you had "oriented" the original torus , Eg : using a blue Circle on the "top" & a red Circle on the "bottom" , then these two Circles [which are "separated" originally] will become "entangled" in the twisted torus ! – Prem Oct 26 '22 at 15:59
-
It's homeomorphic (and diffeomorphic) to the original torus, so I would say no. – Dark Malthorp Oct 26 '22 at 15:59
-
You don't really need to make a torus then cut out a disk to make a cylinder. Just start with a cylinder. – Randall Oct 26 '22 at 16:09
-
Without proofs...? @Prem – Bob Dobbs Oct 26 '22 at 16:15
-
In case this question is motivated by the same problem as your other question: The mapping you describe is a diffeomorphism but is not "isotopic to the identity." – Andrew D. Hwang Oct 26 '22 at 18:04
-
No Proof , only "Intuition" in my Answer Post , @BobDobbs – Prem Oct 27 '22 at 11:07
-
Then can I prove this by using a rubber torus, showing my twisting powers? @Prem – Bob Dobbs Oct 27 '22 at 11:33
-
1I do not know about your twisting Powers , you can best answer that ! [ If you want to say something ( or Post some Answer ) then better to do that Directly , rather than obliquely , I am bad at guessing ! ] I had earlier made a "Quick" Comment & your response made me Post my Answer ! @BobDobbs – Prem Oct 27 '22 at 12:26
-
If you really want to have some fun, consider a torus of non-circular cross-section. Some examples are show here: http://old.nationalcurvebank.org//moebius2/moebius2.htm. – Cye Waldman Oct 27 '22 at 15:21
1 Answers
Here is my way to look at it intuitively :
CASE 1 :
We can take a sheet with 4 sides (Dimension : $1$ Unit $\times$ $1$ Unit) and stick or glue a Pair of Opposite Sides to get a Cylinder.
Then we can stick or glue the other Pair of Opposite Sides (1A) to get a torus.
Having the Cylinder , we can stick or glue after giving a twist of $180^0$ (1B) or a twist of $360^0$ (1C) , we will still get the torus.
CASE 2 :
With a Variation :
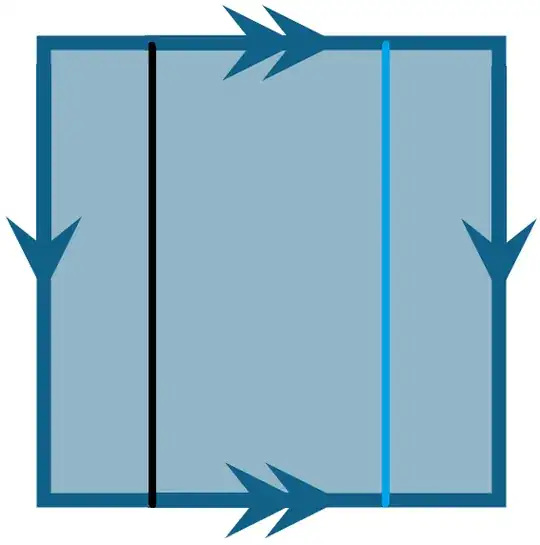
When we have the Cylinder , we can Draw a Black line on the sheet , top to bottom , then we can Draw a Blue line ( Parallelly ) with Distance $1/2$ Unit between the 2 lines.
Now , we can stick or glue the Pair of Opposites sides (2A) with no twist , we will get the same torus with the Black line looping around AND the Blue line looping around.
We have 2 untangled lines here !
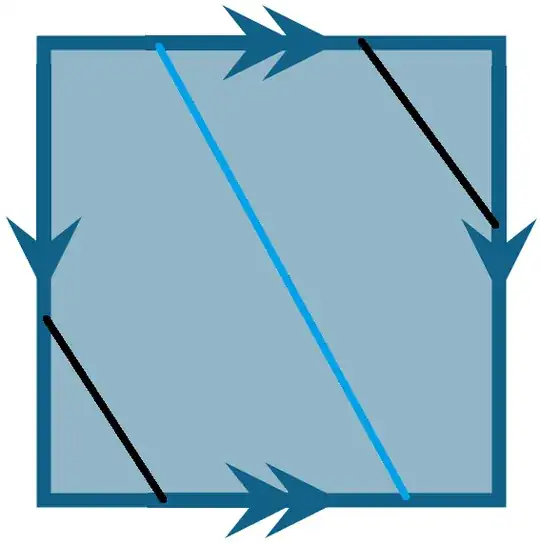
Having the Cylinder , if we stick or glue after giving a twist of $180^0$ (2B) we will see that the Black line merges with (connects to) the Blue line which then merges with (connects to) the Black line.
We have a Single line !
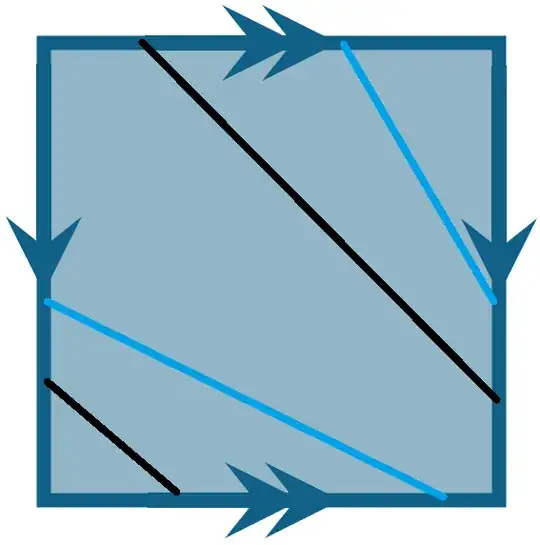
Back to the Cylinder , if we stick or glue after giving a twist of $360^0$ (2C) we will see that the Black line merges with itself but it is winding around the torus. Likewise, the Blue line will merge with itself after winding around.
We have 2 tangled lines here !
In All Cases , (1A) (1B) (1C) (2A) (2B) (2C) , we get the torus but the lines are not matching in (2B) & (2C) !
We can see that with "the line Diagrams" :
(1A) (1B) (1C) with no lines :

(2A) no twist :
(2B) $180^0$ twist :
(2C) $360^0$ twist :
Here is a Course & a Paper [ material for reference ] to make sense of "the line Diagrams" :
https://oertx.highered.texas.gov/courseware/lesson/3362/overview
https://mathcircle.berkeley.edu/sites/default/files/handouts/2018/topology_of_surfaces_2018_0.pdf
- 14,696