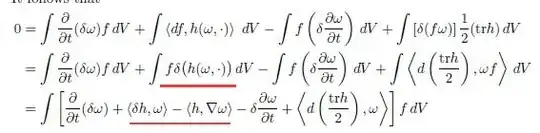How to show $\delta(h(\omega, \cdot)) = \langle \delta h, \omega \rangle -\langle h, \nabla \omega \rangle $?

Question

Picture below is from Topping's 37th page of Lectures on the Ricci flow. I try to show
$$ \delta(h(\omega, \cdot)) = \langle \delta h, \omega \rangle -\langle h, \nabla \omega \rangle $$ $\delta$ is divengence. For tensor $T$, $\delta(T)= -tr_{12} (\nabla T)$. $\omega$ is 1-form. $-h^{ij}= \partial_t g^{ij}$.

What I try: Assume $h=h_{ij}dx^i\otimes dx^j, \omega= \omega_i dx^i$. First, $$ h(\omega, \cdot) = \omega_i h_j^i dx^j $$ therefore \begin{align} \delta (h(\omega, \cdot)) &= -tr_{12} \nabla (\omega_i h_j^i dx^j) \\ &= -g^{ab}[\nabla _a (\omega_i h_j^i dx^j)] \partial_b \tag{1}\\ &= -g^{ab}[\frac{\partial \omega_i}{\partial x_a}h_b^i + \omega_i \frac{\partial h_b^i}{\partial x_a}- \omega_i h_k^i \Gamma_{ab}^k] \end{align} Second, since $$ \delta h = -g^{ab}[\partial_a h_{bk} - \Gamma_{ab}^l h_{lk} -\Gamma_{ak}^l h_{bl}] dx^k $$ I have $$ \langle \delta h, \omega \rangle = -g^{ab}[\partial_a h_{bk} - \Gamma_{ab}^l h_{lk} -\Gamma_{ak}^l h_{bl}] g^{kc}\omega_c \tag{2} $$ Third, since $$ \nabla \omega =(\partial_i \omega_j - \omega_k \Gamma_{ij}^k) dx^i\otimes dx^j $$ I have $$ \langle h, \nabla \omega \rangle = h^{ij}(\partial_i \omega_j - \omega_k \Gamma_{ij}^k) \tag{3} $$ where $h^{ij}= h_{ab} g^{ai}g^{bj}$.

Last, from (1), (2), (3), I have $$ \langle \delta h, \omega \rangle - \langle h, \nabla \omega \rangle = \delta (h(\omega, \cdot)) +g^{kc}\Gamma_{ak}^l h_l^a \omega_c + h^{ij}\omega_k\Gamma_{ij}^k \tag{4} $$ Obviously, from (4), I can't get the red line.

(PS: I omit many computational details, it really be fussy to input. I feel the key point is contained. The answer maybe complex, if so, a picture of handwritten draft is enough for me, thanks.)

Answer 1

This calculation can look very simple, if you can accept that the divergence (codifferential) $\delta \omega$ of a (tensor-bundle-valued) $k$-form $\omega$ can be expressed using the abstract index notation with the following formula $$ (\delta \omega)_{a_2 \dots a_k} = - \nabla^{a_1} \omega_{a_1 a_2 \dots a_k} $$ where $\nabla$ can be any torsion-free connection, and the sequentially numbered indices are always assumed to be anti-symmetrized. The Levi-Civita connection, that you are using, is torsion-free, so it is safe to stick with it.

Let's do the calculation for a $1$-form $\omega_a$, and some symmetric tensor $h_{a b}$, using the metric $g_{a b}$ and its inverse $g^{a b}$ freely to raise and lower indices without mention:

$$ - \delta ( h(\omega, \cdot) ) = \nabla^a (h_a{}^b \omega_b) = (\nabla^a h_a{}^b) \omega_b + h_a{}^b \nabla^a \omega_b = -\langle\delta h, \omega \rangle + \langle h, \nabla \omega \rangle $$ which is equivalent to the sought identity. The second equality in the above equation is an application of the Leibniz rule, and the third equality comes from the change of notation: $$ -\langle\delta h, \omega \rangle = g^{b c}(\nabla^a h_{a b}) \omega_c $$ and $$ \langle h, \nabla \omega \rangle = g^{a c} g^{b d} h_{a b} \nabla_c \omega_d $$

I hope that this helps.