Let $\alpha$ be a $p$-form on an $n$-manifold $M$. I read somewhere that the codifferential $\delta\alpha$ of $\alpha$ can be expressed in terms of covariant derivatives as follow: \begin{align} (\delta\alpha)_{i_1\cdots i_{p-1}}=-g^{jk}\nabla_j\alpha_{ki_1\cdots i_{p-1}} \end{align} I would like to know how to prove this. Since only the definition of $\delta$: \begin{align} \delta\alpha=(-1)^{np+n+1}*d*\alpha \end{align} (where $*$ is the Hodge star operator) was given to me (I'm aware that $\delta$ is usually defined as the adjoint of $d$, but this is the definition I was given; nevertheless, both can be assumed here), and the computation of $*\alpha$ usually involves the factor $\sqrt{\det g_{ij}}$, I'm not sure how to proceed to obtain the expression above in terms of only the covariant derivatives.
Thanks in advance for any comment, hint, and answer.
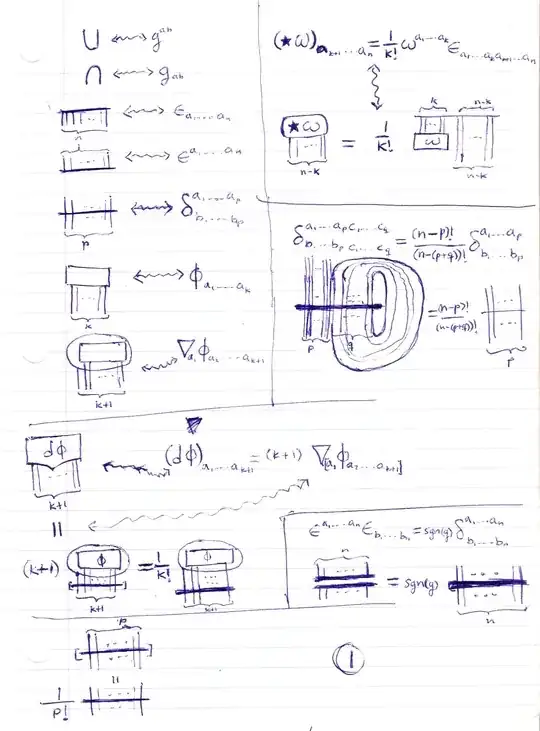
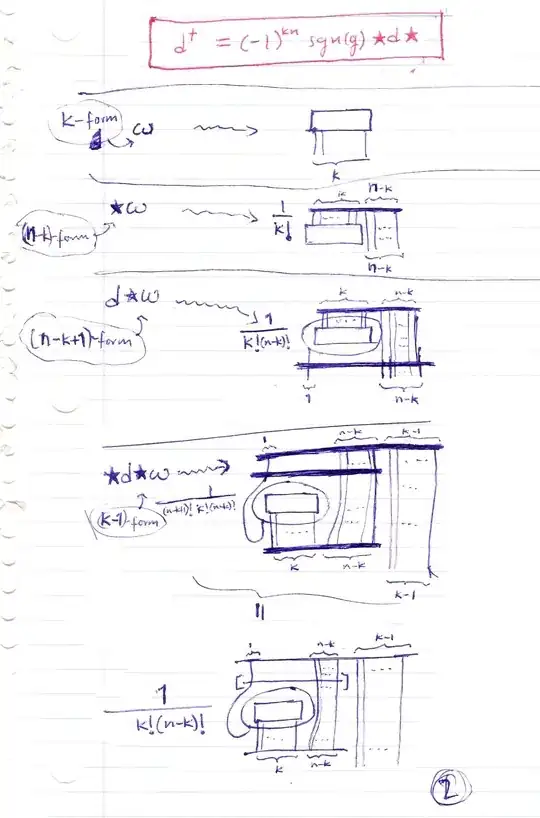
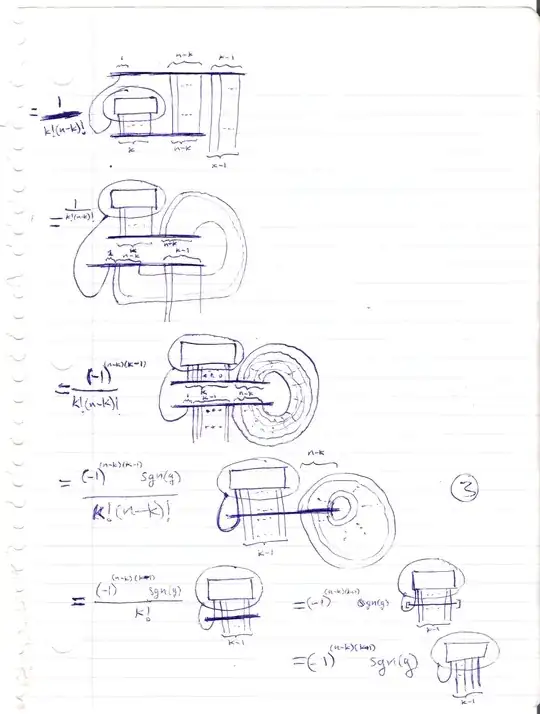
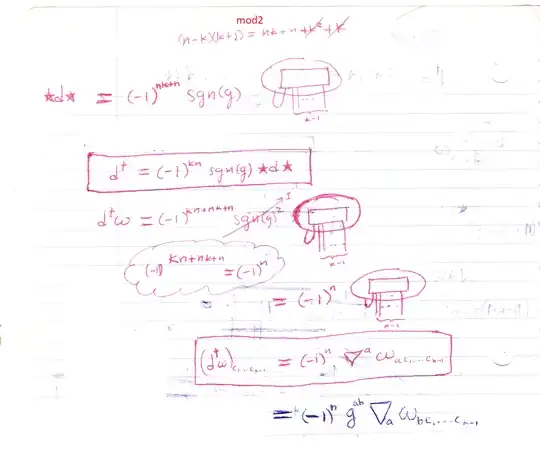
Using it the calculation is almost immediate.
– Jackozee Hakkiuz Jun 22 '18 at 09:42