3

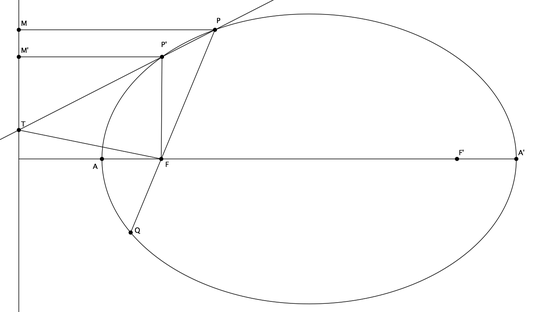
Is there a general proof for this?

The portion of the tangent to any conic intercepted between the point of contact and the directrix subtends a right angle at the focus of the conic?

For parabola, it can be solved this way: the tangent at $P=(at^2, 2at)$ is $ty = x + at^2$. This meets the directrix at the point $Q=(-a,a(t^2 - 1)/t)$. Now, $\text{Slope of }SQ\times\text{Slope of }SP = -1$. Hence, $∠PSQ = 90°$. A similar way of writing the parametric coordinates and equating the product of slopes to $-1$ yields the desired result for other conics.

But is there a geometric proof for any general conic?

Intelligenti pauca
  • 55,765
Atharv Kapila
  • 127
  • 5

1 Answers1

6

The theorem we want to prove can be restated as follows:

If the tangent to a conic at any point $P$ intersects the directrix at point $T$, and F is the corresponding focus, then $\angle PFT$ is a right angle.

Let $P'$ be a point on the conic near to $P$ (see figure below) and suppose line $PP'$ to intersect the directrix at $T$. Let then $M$, $M'$ be the orthogonal projections of $P$, $P'$ on the directrix, and $Q$ a point on line $PF$ produced.

As triangles $TPM$, $TP'M'$ are similar we have: $$ TP:TP'=MP:MP'=FP:FP' $$

and this implies, by the angle bisector theorem applied to triangle $FPP'$, that $TF$ bisects the exterior angle $\angle P'FQ$.

In the limit $P'\to P$, line $PT$ tends to the tangent at $P$ and $\angle P'FQ$ tends to $\angle PFQ$, which is two right angles. Therefore $\angle PFT$, which is the limit of $\angle P'FT$, is one half of $\angle PFQ$, that is a right angle, as it was to be proved.

enter image description here

Intelligenti pauca
  • 55,765