Alternate geometrical proof that tangent bisects angle of parabola

Question

I'm trying to understand the proof hinted at by the comment on the main post here:

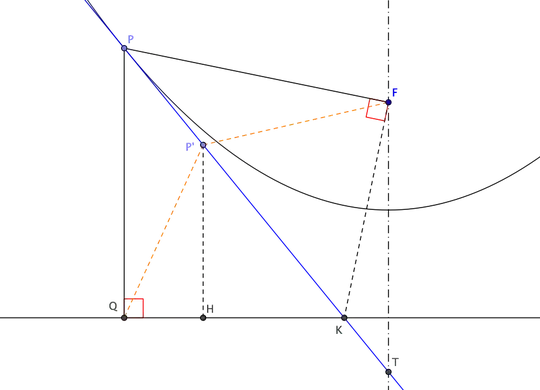
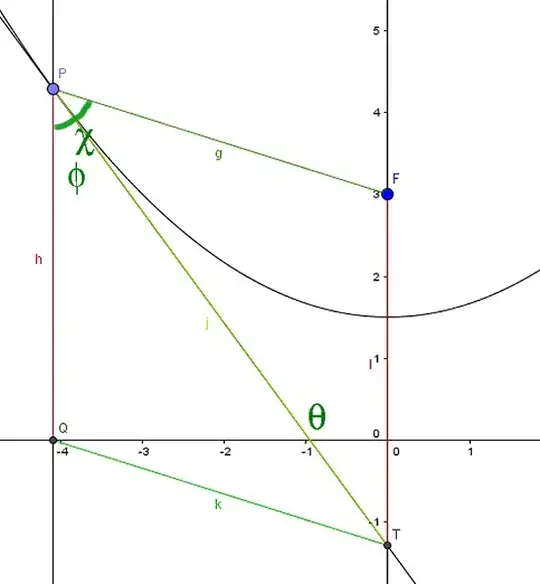
A slightly different way to prove it is to consider the perpendicular bisector of FQ. Because it is a parabola, P must lie on this perpendicular bisector, and for the same reason (this needs a small effort) no other point of the parabola lies on this perpendicular bisector. Then prove that it is a tangent.

I got the fact that $P$ must lie on the perpendicular bisector, we can argue by the property that distance to focus of point= distance of point to directrix. But, how do I show that no other point lies in common with it and parabola, then further, that the line is a tangent?

Possible proof: It must be that if there is another point, then the shortest distance along the common normal line must be zero. However, notice that the normal of the parabola is a bijective function with the parameter, i.e: a given normal has a very specific parameter value which would output it. Hence, it follows that there can only be one parameter value where the normal are in common.

I am not sure if the above explanation is rigorous though.

Intelligenti pauca · Accepted Answer · 2021-08-05T21:51:23.603

3

There are several ways to prove that the tangent at $P$ bisects $\angle FPQ$ (see figure).

The simplest one is probably proving the converse (and I think this is also the proof hinted at in that comment): if line $PT$ is the bisector of $\angle FPQ$, then it touches the parabola only at $P$, all its other points being external to the parabola, and is thus tangent. This follows from a simple observation: if you take any point $P'\ne P$ on line $PT$ and its projection $H$ on the directrix, then $FP'=P'Q>P'H$ and $P'$ is then outside the parabola.

Another way requires to prove as a lemma that $\angle PFK=90°$, where $K$ is the intersection of the tangent at $P$ with the directrix (and this is true for all conic sections, not only parabolas). From that it follows that $\triangle PFK\cong \triangle PQK$ and $PK$ is thus the bisector of $\angle FPQ$.

edited Aug 05 '21 at 21:51

answered Aug 05 '21 at 14:56

Intelligenti pauca

55,765

Hmm I had a similar idea but how would one justify $P'Q>P'H$, it is clear from geometry but can an explicit written reason be given? – Clemens Bartholdy Aug 06 '21 at 08:33
relevant – Clemens Bartholdy Aug 06 '21 at 08:39
1

Well, hypotenuse $P'Q$ is longer than leg $P'H$, because in any triangle the side opposite the greater angle is greater. – Intelligenti pauca Aug 06 '21 at 14:33
Excellent, thank you. – Clemens Bartholdy Aug 06 '21 at 14:37
Why is FP' = P'Q ? @Intelligentipauca – Paracetamol Jun 25 '22 at 15:59
@Paracetamol Because triangles $FPP'$ and $QPP'$ are congruent. – Intelligenti pauca Jun 25 '22 at 17:14
Thanks understood , can we similairily do in other proof problems proving the converse and then say we proved ? Or it will not work in some cases ? @Intelligentipauca – Paracetamol Jun 25 '22 at 19:19
@Paracetamol It doesn't always work. It does in this case, just because the bisector of an angle is unique and the tangent at $P$ is unique too. – Intelligenti pauca Jun 25 '22 at 20:37
1

@Paracetamol To be rigorous, one should end the proof with a RAA argument: suppose the tangent at $P$ is NOT the bisector; by the above proof, however, the bisector IS a tangent at $P$, hence you would have two different tangents at the same point, which is absurd. – Intelligenti pauca Jun 25 '22 at 20:43
Hmm finally understood what you meant thanks @Intelligentipauca – Paracetamol Jun 26 '22 at 20:04

score 1 · Answer 2 · 2021-08-08T08:47:50.423

The parabola in the diagram from the linked page has the equation $ \ y = \frac{x^2}{4f} + f \ , $ with $ \ f \ $ being the distance from the vertex to the directrix on the $ \ x-$ axis. So the slope of the tangent line at $ \ P (x_0 , \frac{x_0^2}{4f} + f) \ $ is $ \ \frac{x_0}{2f} \ $ . The line through the focus $ \ F \ $ and the point $ \ P \ $ has the slope $$ \ \frac{[\frac{x_0^2}{4f} + f] - 2f}{x_0} \ = \ \frac{x_0}{4f} - \frac{f}{x_0} \ \ . $$ The tangent line then makes an angle $ \ \theta \ $ to the $ \ x-$ axis given by $ \ \tan \theta \ = \ \frac{x_0}{2f} \ ; $ this makes the angle $ \ \angle QPT \ = \ \phi \ = \ \theta - 90º \ \ , $ so $ \ \cot \phi \ = \ -\frac{x_0}{2f} \ \ . $

The line $ \ PF \ $ makes an angle $ \ \psi \ $ to the $ \ x-$ axis , so $ \ \angle QPF \ = \ \chi \ = \ \psi - 90º \ \ $ has $ \ \cot \chi \ = \ - \left[ \ \frac{x_0}{4f} - \frac{f}{x_0} \ \right] \ \ . $

The double-angle formula for cotangent is readily shown to be $$ \cot 2\alpha \ \ = \ \ \frac{\cot^2 \alpha \ - \ 1}{2 \ \cot \alpha} \ \ . $$ Applying this, we obtain $$ \cot 2\phi \ \ = \ \ \frac{\left( -\frac{x_0}{2f} \right)^2 \ - \ 1}{2 \ · \ \left( -\frac{x_0}{2f} \right)} \ \ = \ \ -\frac{f}{x_0} · \ \left[ \ \left( \frac{x_0}{2f} \right)^2 \ - \ 1 \ \right] \ \ = \ \ \frac{f}{x_0} \ - \ \frac{x_0}{4f} \ \ = \ \ \cot \chi \ . $$

Hence, the tangent line $ \ PT \ $ bisects the angle $ \ \angle QPF \ \ . $ [Sorry that it's not a purely geometric argument...]

Thanks for the help, but I still am seeking a geometric arguement — Clemens Bartholdy, Aug 05 '21 at 08:12
Assuming that a light ray from the focus will travel on a vertical line after reflection, is the same as assuming what you want to prove. One usually does the reverse: from the angle bisecting property of the tangent, the reflection behaviour described above can be derived. — Intelligenti pauca, Aug 08 '21 at 08:45
While I'll say that that isn't the way I've seen the reflection principle obtained, I will withdraw the argument and try to find a different approach. — , Aug 08 '21 at 08:49

Alternate geometrical proof that tangent bisects angle of parabola

2 Answers2

Linked