1

I discovered a new method for drawing a tangent to a conic section at a point on it using GeoGebra about two months ago, but I haven't been able to prove it. Any help would be appreciated.

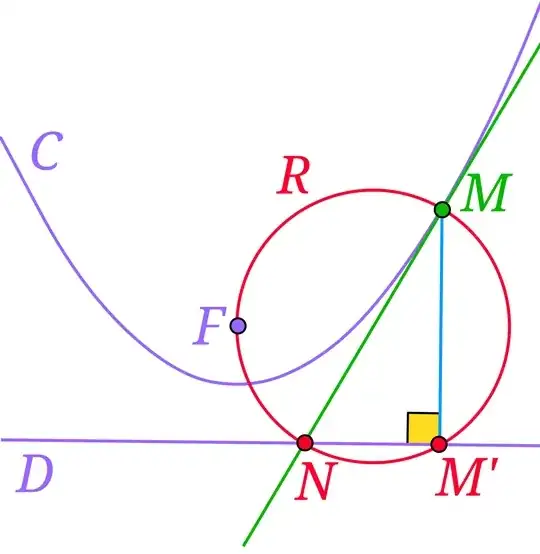
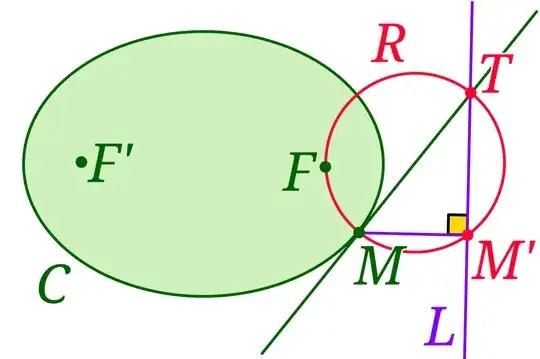
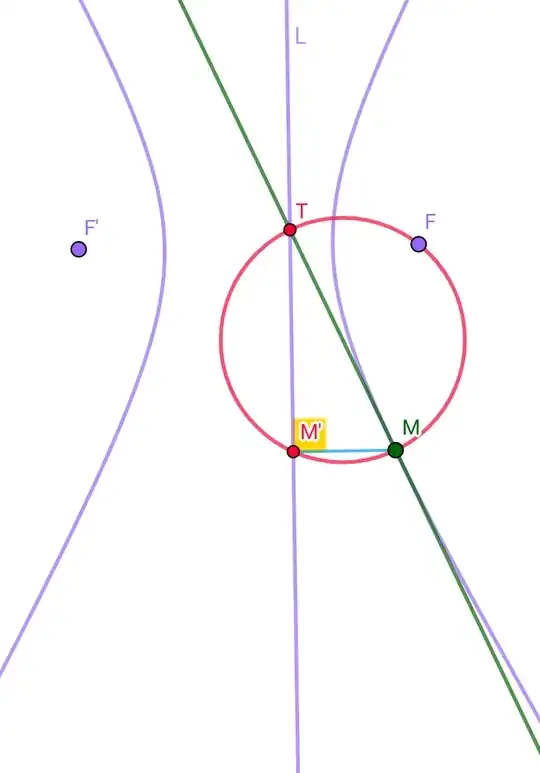
Let C be a conic section with one of its foci at F, and let M be a point on C. Let L be the directrix of C associated to focus F. We want to draw a tangent to C at M.

To do this, we first find the projection M' of point M onto L and draw the circle passing through points M, M', and F. Then, we find the point T where this circle intersects L at a different point than M', and draw the line MT. This line is the desired tangent.

Of course the case of a parabola is self-evident, and the difficulty is to prove the order for both a hyperbola and an ellipse.

enter image description here

enter image description here enter image description here

Intelligenti pauca
  • 55,765
زكريا حسناوي
  • 4,060
  • 7
  • 25
  • "A point in the circumference of $P$"? You probably meant "a point on $P$". Also, by "the line $L$ is the guide $P$ following the focal point $F$" did you mean "the directrix related to the focus $F$"? – jjagmath Jun 26 '23 at 17:33
  • "the directrix of C that passes through the focus F"? The directrices of a conic does not pass through the foci. – jjagmath Jun 26 '23 at 19:18
  • This is a famous property of conic sections. – Intelligenti pauca Jun 26 '23 at 20:13
  • At first it was translated via Google, it turned out that there were errors, and the second time it was translated via chat gpt and also it turned out that there are errors, I do not know the English language and I do not know how to avoid errors, thanks for correcting my question, and thanks for pointing out the existence of a previous method, I was not aware with it – زكريا حسناوي Jun 26 '23 at 22:43
  • 2
    Even if the question is a duplicate, I encourage you to explore further. What you come up with alone, no one will take away from you. I also really appreciate that you try to write in English, even if it is foreign to you. – Viera Čerňanová Jun 27 '23 at 09:43
  • 1
    Thanks for the encouragement, I'll be posting more of my work from time to time – زكريا حسناوي Jun 27 '23 at 13:08

0 Answers0