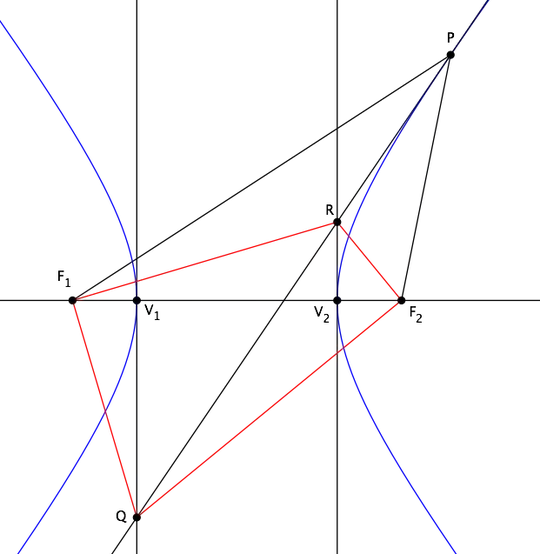
Here is the construction I am looking at.
Let $F_1$ and $F_2$ with respective vertices $V_1$ and $V_2$. Let $P$ be a point be closer to $F_2$ than $F_1$. Tangents are drawn from from $V_1,$ $V_2,$ and $P.$ As $V_1$ and $V_2$ are parallel the only intersections between the tangents come from the tangents $P/V_1$ and $P/V_2.$ Let these intersections be $Q$ and $R.$ Now, $\angle RF_1Q=90^{\circ}.$
Here is a picture:
This is the fact I want to prove geometrically. Most likely a straightforward analytical solution exists but I am more interested in how to approach this synthetically.
I've tried angle chasing based on the fact that the tangent $P$ bisects the angle $\angle F_1PF_2.$ But both my attempts at finding $\angle RF_1Q$ directly and trying to prove $F_1RF_2Q$ concyclic have failed.
Similarly, I've had trouble trying to find more about geometric properties of hyperbolas online as most websites discuss hyperbola using coordinates which I am trying to avoid here.