3

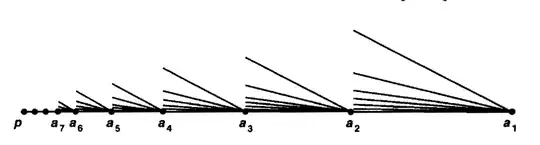
Consider the "infinite broom" $X$ pictured in figure below. Show that $X$ is not locally connected at $p$, but is weakly locally connected at $p$.[Hint: Any connected neighborhood of $p$ must contain all the points $a_i$]

infinite broom

For simplicity, I took, $X\subset \mathbb{R}^2$, such that $p=0\times 0$ and $a_1=1\times 0$, so that consider the subspace topology of $X$ in $\mathbb{R}^2$

First let, $X=\bigcup_{i=1}^{\infty}X_i$, where $X_i$ is the "infinite broom" inside $(a_{i+1},a_i]$. Note that $X_i$ 's are path connected.

Now consider a connected nbh of $p$, say $U$. It contains $a_n$ and $a_{n+1}$ but not $a_{n-1}$. So the open set contains the upper bound point $\overline{a_n+\epsilon}\times c$, for some $\epsilon,c>0$. So to have $U$ connected, we need $a_{n-1}$ inside $U$. In this way we need $a_1$ to be inside $U$. Then $U$ must contain the segment $(0\times 0,1\times 0)$, which contradicts the definition of locally connectedness at a point.

Can anyone check if this is ok or not?

Altough, don't know how to show weakly local connectedness at $p$.

PatrickR
  • 7,165
topology_001
  • 341
  • I don't understand why nobody has wrote anything. Am I asking a wrong question? Am I asking a lot? – topology_001 Sep 22 '17 at 02:28
  • May I ask which definition of local connectedness do you use here since I notice the definition in Munkres is 'A space $X$ is said to be locally connected at $x$ if for every neighborhood $U$ of $x$, there is a connected neighborhood $V$ of $x$ contained in $U$, while the definition on Wikipedia requires the connected neighborhood to be open. – Wembley Inter Nov 20 '18 at 00:35
  • @WembleyInter Neighborhoods are defined to be open sets – Dylan Jun 09 '20 at 03:02

2 Answers2

6

Your part on connectedness is quite ok, but it needs some clarification.

X is not locally connected

Because of the definition of $X$ as the space in the picture, it can be assumed that $X$ is in the real plane and has the subspace topology.

Consider a (small) open neighbourhood of $p$, so an open ball $B$, such that there exist $n \in \mathbb{N}$ with $a_n$ not in $B$, but $a_{n+1}$ is in $B$, then because the ball is open there will be some part of some stalks of the $n$th-broom lying in $B$, this implies the non-local connectedness of the space.

Remark: We want a small neighbourhood because we want to show a local property, then the fact that such $n$ exists is a tautological statement about what an open ball is

X is weakly connected in $p$

We have to show that $X$ is weakly connected in $p$

To be weakly connected in $p$ means that given an open neighbourhood of $p$, I can find a subset of this neighbourhood such that $p$ is in the interior of this subset, and this subset is connected.

So, the difference with local connectedness is that this subset needs not to be open.

Given a small neighbourhood $B_\epsilon$ of $p$ of radius $\epsilon$, then there exist $N \in \mathbb{N}$ such that $a_n \in B_\epsilon$ for all $n > N$, then I can take the subspace of $X$ including $p$ and every broom until the $n$th-one , $n>N$, this space is (obviously not open but) connected and its interior contains $p$, so $X$ is weakly connected in $p$.

Remark: Note that an interior point is with respect to $X$, so using the induced topology

Alessio Ranallo
  • 422
  • May I ask which definition of local connectedness do you use here since I notice the definition in Munkres is 'A space $X$ is said to be locally connected at $x$ if for every neighborhood $U$ of $x$, there is a connected neighborhood $V$ of $x$ contained in $U$, while the definition on Wikipedia requires the connected neighborhood to be open. – Wembley Inter Nov 20 '18 at 00:33
-2

From the definition

Take end point $(\frac{1}{n+1},\frac{1}{m}) \in B(p, \epsilon$) for $m \ge n$ .But $(\frac{1}{n+1},\frac{1}{m})=(\frac{1}{n+1},\frac{1}{n}) \cup(\frac{1}{n+1},\frac{1}{m})$

Now visualize the diagram of broom

you will see $a_n= (1/n,0) \in (\frac{1}{n+1} , \frac{1}{m})$ and $a_n \notin(\frac{1}{n+1},\frac{1}{n})$

This implies $X$ is not locally connected at $p$

jasmine
  • 15,021