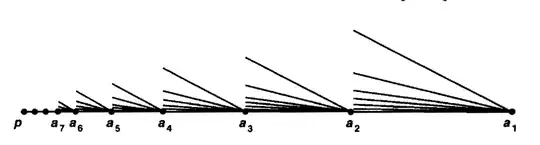
Consider the "infinite broom" $X$ pictured in figure below. Show that $X$ is weakly connected at $p$.
My attempt : I found the answer here.But im not satisfied with answer
My attempt : Consider $X$ to be a subspace of $\mathbb{R}^2$ with $p=(0,0) $ and each $a_n$ on the positive $x-$ axis .Let us assume $V$ as an open set in $\mathbb{R}^2$ and $U$ be an open neighbhood of $p$
By the definition of subspace topology $U= X \cap V $ is open/closed. This implies $V$ contains an open ball $B(p,a_n)$.
Now take connected subspace $Y$ of $X$ where $Y= U'\cup \{a_{n+1}\}$ because $U' \cap a_{n+1} \neq \emptyset$ where $U'=X \setminus B(p,a_{n+1})$
Therefore $Y \subset U$ and contains the neighbhorhood $X \cap B(p,a_{n+1})$ of $p$
Now by the Munkres book definition $X$ is weakly locally connected at $p$
A space $X$ is said to be weakly locally connected at $x$ if for every neighborhood $U$ of $x$, there is a connected subspace of $Y$ contained in $U$ that contains a neighborhood of $x.$
Note : Take $x=p$
Is my proof is correct or not ?