Definition of Infinite Broom
In wikipidea it is written that
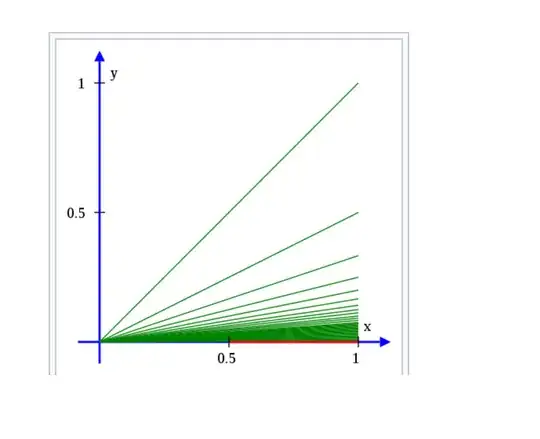
The infinite broom is the subset of the Euclidean plane that consists of all closed line segments joining the origin to the point $(1, 1/n)$ as n varies over all positive integers, together with the interval $(1/2, 1]$ on the x-axis
Diagram of infinite broom
My thinking : From the diagram ,we conclude that all the line segment start from $(0,0)$ to $(1,1/n)$ and there is no any line segment start from $(1/2,1]$
I don't understand this sentence together with the interval $(1/2,1$] on the $x$ axis
why together with the interval $(1/2, 1]$ on the x-axis ?