I saw this question today, it asks how many triangles are in this picture.
I don't know how to solve this (without counting directly), though I guess it has something to do with some recurrence.
How can count the number of all triangles in the picture ?
Say that instead of four triangles along each edge we have $n$. First count the triangles that point up. This is easy to do if you count them by top vertex. Each vertex in the picture is the top of one triangle for every horizontal grid line below it. Thus, the topmost vertex, which has $n$ horizontal gridlines below it, is the top vertex of $n$ triangles; each of the two vertices in the next row down is the top vertex of $n-1$ triangles; and so on. This gives us a total of
$$\begin{align*} \sum_{k=1}^nk(n+1-k)&=\frac12n(n+1)^2-\sum_{k=1}^nk^2\\ &=\frac12n(n+1)^2-\frac16n(n+1)(2n+1)\\ &=\frac16n(n+1)\Big(3(n+1)-(2n+1)\Big)\\ &=\frac16n(n+1)(n+2)\\ &=\binom{n+2}3 \end{align*}$$
upward-pointing triangles.
The downward-pointing triangles can be counted by their by their bottom vertices, but it’s a bit messier. First, each vertex not on the left or right edge of the figure is the bottom vertex of a triangle of height $1$, and there are $$\sum_{k=1}^{n-1}=\binom{n}2$$ of them. Each vertex that is not on the left or right edge or on the slant grid lines adjacent to those edges is the bottom vertex of a triangle of height $2$, and there are
$$\sum_{k=1}^{n-3}k=\binom{n-2}2$$ of them. In general each vertex that is not on the left or right edge or on one of the $h-1$ slant grid lines nearest each of those edges is the bottom vertex of a triangle of height $h$, and there are
$$\sum_{k=1}^{n+1-2h}k=\binom{n+2-2h}2$$ of them.
Algebra beyond this point corrected.
The total number of downward-pointing triangles is therefore
$$\begin{align*} \sum_{h\ge 1}\binom{n+2-2h}2&=\sum_{k=0}^{\lfloor n/2\rfloor-1}\binom{n-2k}2\\ &=\frac12\sum_{k=0}^{\lfloor n/2\rfloor-1}(n-2k)(n-2k-1)\\ &=\frac12\sum_{k=0}^{\lfloor n/2\rfloor-1}\left(n^2-4kn+4k^2-n+2k\right)\\ &=\left\lfloor\frac{n}2\right\rfloor\binom{n}2+2\sum_{k=0}^{\lfloor n/2\rfloor-1}k^2-(2n-1)\sum_{k=0}^{\lfloor n/2\rfloor-1}k\\ &=\left\lfloor\frac{n}2\right\rfloor\binom{n}2+\frac13\left\lfloor\frac{n}2\right\rfloor\left(\left\lfloor\frac{n}2\right\rfloor-1\right)\left(2\left\lfloor\frac{n}2\right\rfloor-1\right)\\ &\qquad\qquad-\frac12(2n-1)\left\lfloor\frac{n}2\right\rfloor\left(\left\lfloor\frac{n}2\right\rfloor-1\right)\;. \end{align*}$$
Set $\displaystyle m=\left\lfloor\frac{n}2\right\rfloor$, and this becomes
$$\begin{align*} &m\binom{n}2+\frac13m(m-1)(2m-1)-\frac12(2n-1)m(m-1)\\ &\qquad\qquad=m\binom{n}2+m(m-1)\left(\frac{2m-1}3-n+\frac12\right)\;. \end{align*}$$
This simplifies to $$\frac1{24}n(n+2)(2n-1)$$ for even $n$ and to
$$\frac1{24}\left(n^2-1\right)(2n+3)$$ for odd $n$.
The final figure, then is
$$\binom{n+2}3+\begin{cases} \frac1{24}n(n+2)(2n-1),&\text{if }n\text{ is even}\\\\ \frac1{24}\left(n^2-1\right)(2n+3),&\text{if }n\text{ is odd}\;. \end{cases}$$
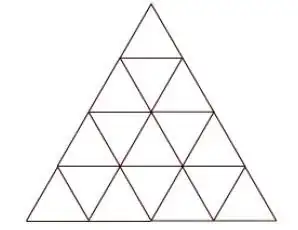
Let $u(n,k)$ denote the number of upwards-pointing triangles of size $k$ included in a triangle of size $n$, where size is a short term for edge length. Let $d(n,k)$ likewise denote the number of down triangles. You can tabulate a few numbers to get a feeling for these. In the following table, row $n$ and column $k$ will contain two numbers separated by a comma, $u(n,k), d(n,k)$.
$$ \begin{array}{c|cccccc|c} n \backslash k & 1 & 2 & 3 & 4 & 5 & 6 & \Sigma \\\hline 1 & 1, 0 &&&&&& 1 \\ 2 & 3, 1 & 1,0 &&&&& 5 \\ 3 & 6, 3 & 3,0 & 1,0 &&&& 13 \\ 4 & 10, 6 & 6,1 & 3,0 & 1,0 &&& 27 \\ 5 & 15,10 & 10,3 & 6,0 & 3,0 & 1,0 && 48 \\ 6 & 21,15 & 15,6 & 10,1 & 6,0 & 3,0 & 1,0 & 78 \end{array} $$
Now look for patterns:
Using these rules, you can extend the table above arbitrarily.
The important fact to note is that you get the same sequence of $1,3,6,10,15,21,\ldots$ over and over again, in every column. It describes grids of triangles of same size and orientation, increasing the grid size by one in each step. For this reason, those numbers are also called triangular numbers. Once you know where the first triangle appears in a given column, the number of triangles in subsequent rows is easy.
Now take that sum column to OEIS, and you'll find this to be sequence A002717 which comes with a nice formula:
$$\left\lfloor\frac{n(n+2)(2n+1)}8\right\rfloor$$
There is also a comment stating that this sequence describes the
Number of triangles in triangular matchstick arrangement of side $n$.
Which sounds just like what you're asking.
If you want to know how to obtain that formula without looking it up, or how to check that formula without simply trusting an encyclopedia, then some of the references given at OEIS will likely help you out:
edit: I tried to write this as a generalization of the simpler case of counting the small triangles, but clearly didn't anticipate the problems that would arise. My proposed solution doesn't work, as it counts straight lines as well as triangles. It can be corrected in a number of different ways, but this just complicates a method which is already inefficient.
Label each corner of each triangle and consider them to be nodes on a graph. You can then write the adjacency matrix for that graph. Because the graph has such a regular structure, the matrix can be worked out easily enough, and scales up nicely. IMPORTANT: two nodes are "adjacent" if they are connected by a straight line, not just a line segment.
Adjacency matrices have the cool property that if you take their product, it tells you how many ways there are to get from one point to another. If you take the cube of the matrix, the diagonal entries will tell you how many ways there are to get from a point back to itself in three moves (i.e. form a triangle).
From there, you just need to take the trace of this matrix, and divide the result by six (since each triangle is counted six times; twice for each corner.)
edit: divide by six, not three.
Let $T_n$ denote the number of triangles when the side-length of the large triangle is $n\geq0$. Then $T_0=0$, $T_1=1$. To obtain a recurssion formula for the $T_n$ we have to distinguish even and odd $n$.
Assume $n=2m$, and let us add a $(2m+1)$'th row of triangles at the bottom. Then each "old" triangle will appear in $T_{2m+1}$, furthermore each "old" gridpoint is a vertex of a triangle with base at the bottom of the new figure, and finally the new bottom gridpoints $z$ serve as vertices of new bottom-up triangles whose sizes are between $1$ and the distance of $z$ from the lower corners of the figure. It follows that
$$T_{2m+1}=T_{2m}+\sum_{k=0}^{2m} (k+1)+2\sum_{k=1}^m k\ ,\qquad(*)$$
and similarly we obtain
$$T_{2m+2}=T_{2m+1}+\sum_{k=0}^{2m+1} (k+1)+2\sum_{k=1}^m k + (m+1)\ .$$
Plugging $T_{2m+1}$ from the first formula into the second we get
$$T_{2m+2}=T_{2m}+2\sum_{k=0}^{2m} (k+1) +(2m+2)+4\sum_{k=1}^m k +(m+1)=T_{2m}+6m^2+11m +5\ .$$
This implies $$T_{2m}=(m-1)m(2m-1)+11{(m-1)m\over2}+5m={1\over2}(4m^3+5m^2 +m)\ ,$$ and using $(*)$ we obtain $$T_{2m+1}={1\over2}(4m^3+11m^2+9m+2)\ .$$ (This coincides with Brian M. Scott's results.)
A lot of complicated answers for a simple problem. That's fine, but we're just trying to solve this simple problem here, not the full generalization of it. Just go by size.
Triangles of size 1 (as in 1 small triangle): 16 Triangles of size 16: 1 (the big triangle) Triangles of size 9: 3, this is pretty clear
This leaves only triangles of size 4, which is probably the only tricky part of the problem. I guess every triangle is either going to have a point at the top and be flat on the bottom, or be flat on the top and have a point on the bottom. Once you recognize this, there's nothing tricky about this part either. There are 6 with the point on top, and 1 with the point on the bottom. So the total is
$$16 + 1 + 3 + 6 + 1 = 27$$
// C snippet for counting tri
//ak13
#include<stdio.h>
int main()
{
unsigned long long int i,n,s,t,k;
scanf("%llu",&t);
for(;t>0;t--)
{
scanf("%llu",&n);
s=0;
k=0;
for(i=0;i<=n;i+=2)
s=s+(i*(i+1))/2;
for(i=1;i<=n;i+=2)
k=k+(i*(i+1))/2;
if(n%2==0)
k*=2;
else
s*=2;
printf("%llu\n",s+k);
}
return 0;
}
The total is $28$. It's $16+8+3+1$ triangles of each size grouping.
