"Number of triangles" for a figure (equilateral triangle; edges divided into $n$ equal sides)

Question

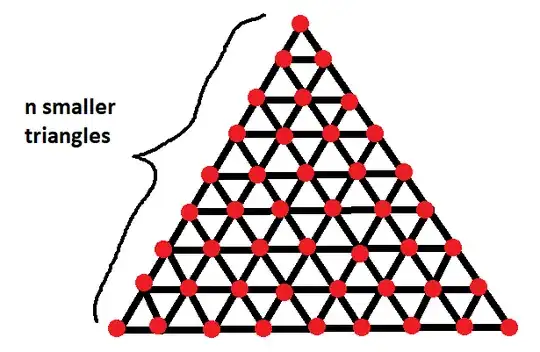
Given $n$, consider the following figure:

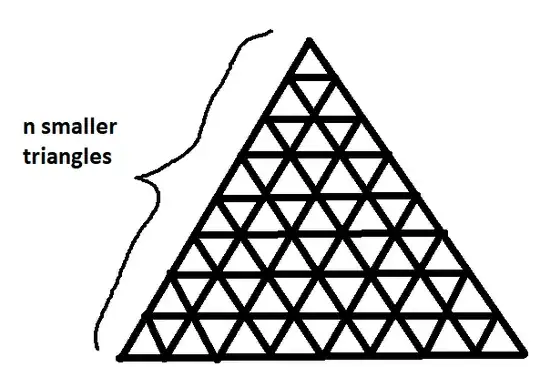
which is formed by placing $n$ equally spaced vertices along the edges of an equilateral triangle and connecting them. The intersection of the lines created will be called the vertices of the figure; the ones in red below:

Question: How many triangles can we make out of the vertices of this figure?

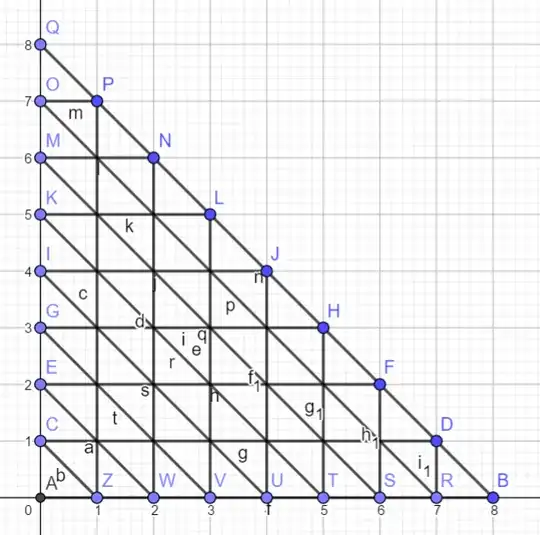
It is more-or-less straightforward to count them for smaller values of $n$. Let $T_n$ be the number of triangles. If we order the vertices by $P_1,P_2,\ldots,P_{\frac{n(n+1)}{2}}$, we can just check for each $P_i,P_j,P_k$ with $i<j<k$ if they are colinear or not. So in the general case we should just count the number of three choices among $P_1,\ldots,P_{\frac{n(n+1)}{2}}$, but then discard the colinear ones.

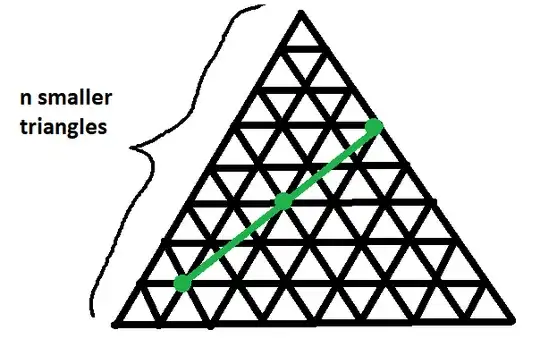
The problem is that we might have some colinear points as below, which I do not know how to deal with (in green):

The original question was asked to me for $n=3$, which is easy to count: $T_3=17$. I though I would at least be able to come um with a recurrence relation for $T_n$ in terms of $T_{n-1}$ and $T_{n-2}$, but I can't (or at least I think such a recurrence I could come up with would be too complicated to be useful).

But I do not know how to tackle the general problem.

---

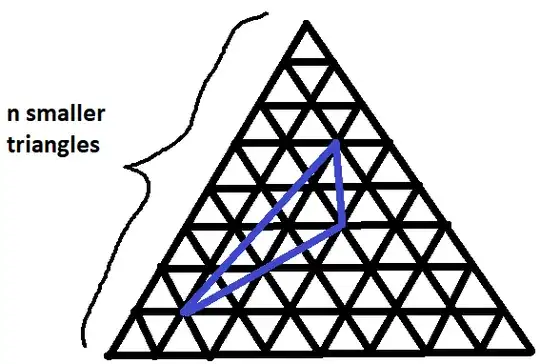
Remark: in this question, there is an answer when only considering the "upwards" or "downwards-pointing" subtriangles, but we allow for subtriangles such as the one below (in blue):

Answer 1

Not an answer, but too long for a comment.

I find it easier to think about if we do an affine transformation that makes the left edge of the triangle vertical. Affine transformations keep the fact that three points are colinear, so we can do that. Your figure then looks like the one below. The nice thing is that the points are on lattice points, with integer coordinates. You can then look at the number of selections of three points that have a common offset from the first to the second and the second to the third.