9

Suppose we have 10 dots arranged in as a triangle as shown below.

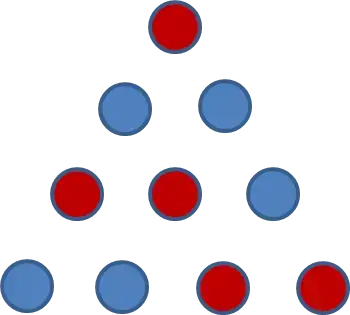
enter image description here

Colour the dots so that some are red and the rest are blue. Show that regardless of how we colour the dots, an equilateral triangle can be formed from three dots of the same colour.

Any advice or clues is greatly appreciated.

Mike Pierce
  • 19,406
Large_Individual
  • 278

5 Answers5

8

Label the dots as

   a
  b c
 d e f
g h i j

Assume it is possible to color the dots so that no equilateral triangles can be formed from dots of same colors. WOLOG, we can assume $e = R$.

Let $\mathcal{E}$ be the collection of $3$ dots which forms an equilateral triangle.

  1. Since $\{ b, f, h \} \in \mathcal{E}$, at least one of $b, f, h$ is $R$.
    Rotate configuration if necessary, we can assume $h = R$.

  2. Since $\{ d, e, h \}, \{ h, e, i \} \in \mathcal{E}$ and $e = h = R$, we have $d = i = B$.

  3. Since $\{ d, i, c \} \in \mathcal{E}$ and $d = i = B$, we have $c = R$

  4. Since $\{ b, e, c \}, \{ e,f,c \} \in \mathcal{E}$ and $e = c = R$, we have $b = f = B$.

  5. Since $\{ a, d, f \} \in \mathcal{E}$ and $d = f = B$, we have $a = R$.
  6. Since $\{ b, g, i \} \in \mathcal{E}$ and $b = i = B$, we have $g = R$.
  7. Since $\{ i, f, j \} \in \mathcal{E}$ and $f = i = B$, we have $j = R$.
  8. Finally $\{ a, g, j \} \in \mathcal{E}$ but $a = g = j = R$, a contradiction!

The decision procedure is illustrated below. The subscript indicate at which step the corresponding color is determined. $$ \color{red}{a_5}\\ \color{blue}{b_4} \quad \color{red}{c_3}\\ \color{blue}{d_2} \quad \color{red}{e_0} \quad \color{blue}{f_4}\\ \color{red}{g_6} \quad \color{red}{h_1} \quad \color{blue}{i_2} \quad \color{red}{j_7}\\ $$

achille hui
  • 125,323
  • Is b-d-f equilateral in your example? Or a-g-c? I'm really not understanding this challenge and all answers seem to actually disprove the assumption. – Anthony May 25 '18 at 00:19
  • @Anthony Neither b-d-f nor a-g-c forms an equilateral triangle. The original $10$ dots is assumed to lie on a standard hexagon lattice. three dots will form an "equilateral triangle" iff they form an true equilateral triangle when placed ideally on this lattice. – achille hui May 25 '18 at 01:23
  • But isn't that just true of any three dots then? Why do the colors matter at all? – Anthony May 25 '18 at 01:29
  • @Anthony That's not true. an equilateral triangle is a triangle with equal sides. As an example, consider triangle bdf. When drawn ideally, its side lengths is having the ratio $bd : df : bf = 1 : 2 : \sqrt{3} \ne 1 : 1 : 1$, so $\triangle bdf$ isn't an equilateral triangle. – achille hui May 25 '18 at 02:58
  • Then how is b-d-f an example of three dots of the same color making an equilateral triangle? "Show that regardless of how we colour the dots, an equilateral triangle can be formed from three dots of the same colour." B-d-f are the same color and don't form an equilateral triangle. Again, I think I may just be missing a crucial element of the challenge. – Anthony May 25 '18 at 03:02
  • @Anthony The claim is "no matter how you color the dots", you can find three dots which forms an equilateral triangle and has the same color. Break the second clause into logical unit, it is $$\text{ EXISTS 3 dots ( "forms an equilateral triangle" AND "has the same color" ))}$$

    it doesn't mean every 3 dots which has the same color will form an equilateral triangle.

    $$\text{ FORALL 3 dots ( "has same color" IMPLIES "forms an equilateral triangle" )}$$

     – achille hui May 25 '18 at 03:36
  • I see. So no matter how you color the dots, there will always be at least one equilateral triangle that can be drawn from three dots of one of the two colors. There could be more, but there will always be one. – Anthony May 25 '18 at 16:28
  • And your final result is the most colored dots of one color where that color forms 0 equilateral triangles, thus proving that even in that scenario, three dots of the other color will still make at least one. – Anthony May 25 '18 at 16:31
  • Given your example, does it prove that "regardless of how we colour the dots, at least two equilateral triangles can be formed from three dots of the same colour."? – Anthony May 25 '18 at 16:33
  • @Anthony No it didn't, When we allow three dots on an equilateral triangle to have same color earlier in the decision process, the argument above doesn't rule out the possibility those 3 dots are the equilateral triangle that has same color. If we want to be sure at least two equilateral triangles can be formed, one probably should ask a computer to brute force go over all possible cases. – achille hui May 25 '18 at 16:42
6

Get some paper and pen and start coloring. Try to avoid a monochromatic triangle, and see that you are forced to make one anyway.

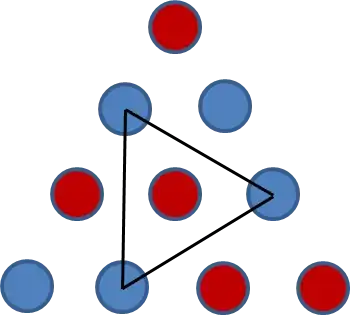
Every triangle must have two of one color and one of the other. Let's choose the largest triangle, as it seems to have the most intersection with the other triangles. As there's nothing special about either color, let there be two blue and one red:

enter image description here

The top most little triangle now has 1 red, so the other two must either be both blue, or one red one blue.

CASE I:

enter image description here

Now we have 3 triangles which have two blue circles, which force their third circle to be red:

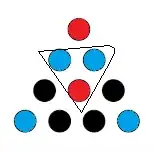
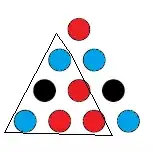
enter image description hereenter image description hereenter image description here

Oh no! We have been forced to make a red triangle.

CASE II

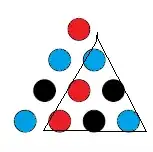
We have one red and one blue in our upper triangle. By symmetry it doesn't matter which is which.

enter image description here

And again we color in what we're forced to to avoid a monochromatic triangle.

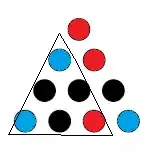
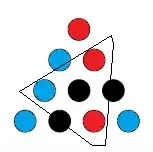
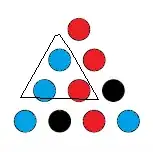
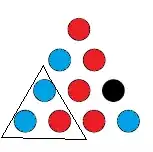
enter image description hereenter image description hereenter image description hereenter image description here

And again we have been forced to make a triangle with all the same color. Thus, no matter how we proceed with the coloring, there is a monochromatic triangle.

Josh B.
  • 3,476
4

The six dots around the center dot form two equilateral triangles. Clearly no five dots can be of the same colour. If both colours occur exactly three times in these six dots then we get an equilateral triangle of one colour by considering the colour of the center dot if necessary. Hence one colour occurs four times and the other twice, and the center colour is the other colour. So the colours form three bands in some direction, and now any colouring of the corner dot yields an equilateral triangle of one colour.

Servaes
  • 67,306
  • 8
  • 82
  • 171
3

Number the dots as follows: $$\matrix{ &&&\color{blue}{\cdot1}&&&\cr &&\cdot2&&\cdot3&&\cr &\cdot4&&\cdot5&&\cdot6&\cr \color{red}{\cdot7}&&\cdot8&&\cdot9&&\color{red}{\cdot10}\cr}$$ We may assume that $\cdot7$ and $\cdot10$ are red, and that $\cdot1$ is blue. Then:

  • $\cdot8$ and $\cdot9$ both red is impossible.
  • $\cdot8$ red and $\cdot9$ blue enforces $\cdot3$ and $\cdot4$ blue, creating a forbidden blue triangle: $$\matrix{ &&&\color{blue}{\cdot1}&&&\cr &&\cdot2&&\cdot3&&\cr &\cdot4&&\cdot5&&\cdot6&\cr \color{red}{\cdot7}&&\color{red}{\cdot8}&&\color{blue}{\cdot9}&&\color{red}{\cdot10}\cr}$$
  • $\cdot8$ and $\cdot9$ both blue enforce $\cdot5$ red. It follows that $\geq1$ of $\cdot2$ and $\cdot4$ as well as $\geq1$ of $\cdot3$ and $\cdot6$ have to be blue. However this is done we obtain a forbidden blue triangle. $$\matrix{ &&&\color{blue}{\cdot1}&&&\cr &&\cdot2&&\cdot3&&\cr &\cdot4&&\color{red}{\cdot5}&&\cdot6&\cr \color{red}{\cdot7}&&\color{blue}{\cdot8}&&\color{blue}{\cdot9}&&\color{red}{\cdot10}\cr}$$
Christian Blatter
  • 232,144
0

Are you sure this is true? I can't find such a triangle in here:

enter image description here

I see $13$ equilateral triangles in here, but none of them have $3$ dots of the same color ... what am I missing?

EDIT

OK, I see what I missed:

enter image description here

Well, take this post as a Hint: there may be more triangles than you think! :)

In fact, there are $15$ equilateral triangles, not $13$

Bram28
  • 103,721
  • 2
    the leftmost on 2nd row, the rightmost on 3rd row and the 2nd one (counting from left) on last row forms a blue triangle. – achille hui May 24 '18 at 12:25
  • @achillehui Yup! Just came out of the shower during which I realized this (why do showers do this to our brains?) :) – Bram28 May 24 '18 at 12:33
  • @Bram28 that's I guess .. when you take shower endorphins are released..or something like that .. I am not sure – Pushparaj May 24 '18 at 12:43